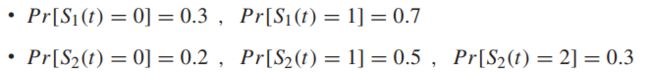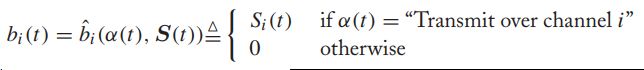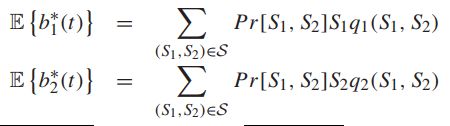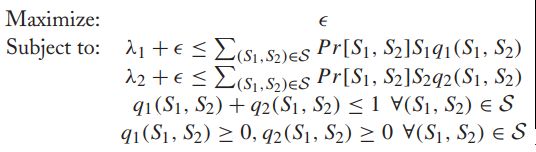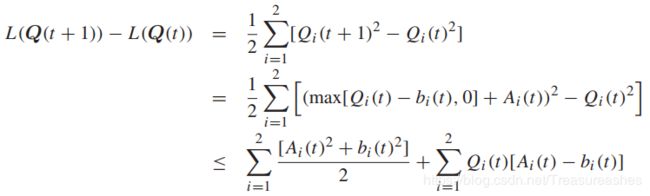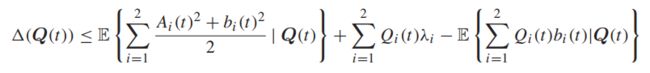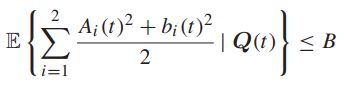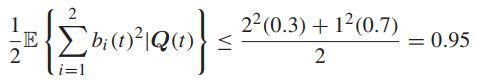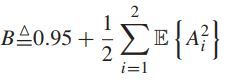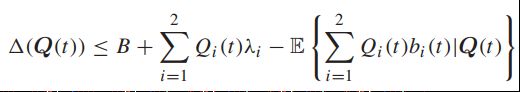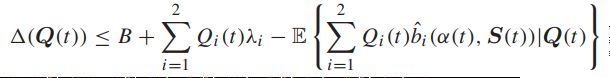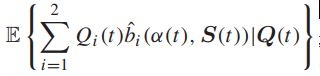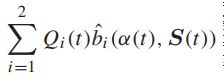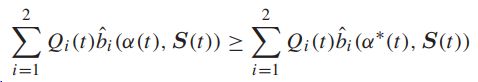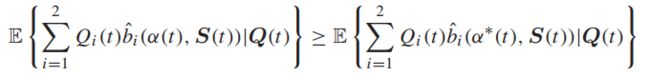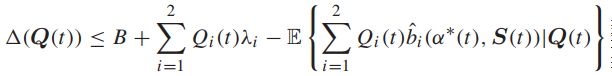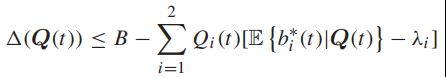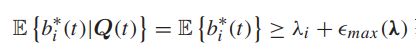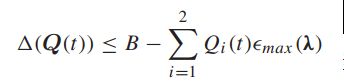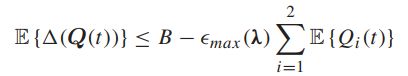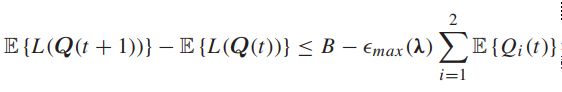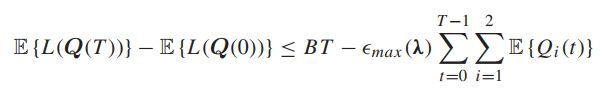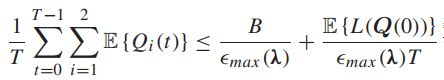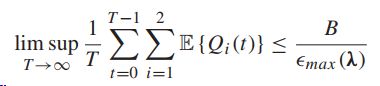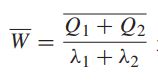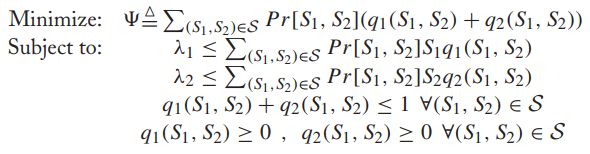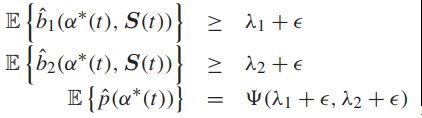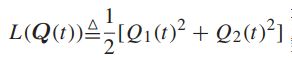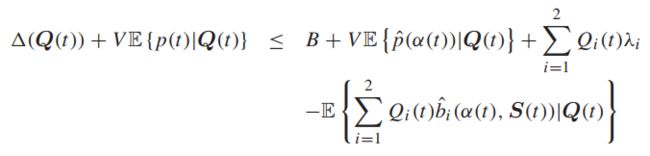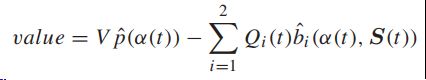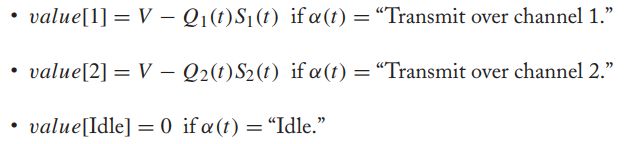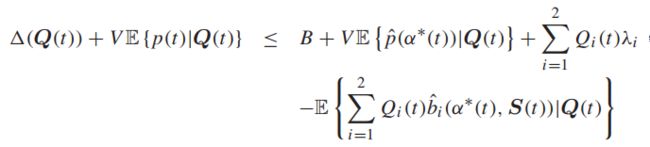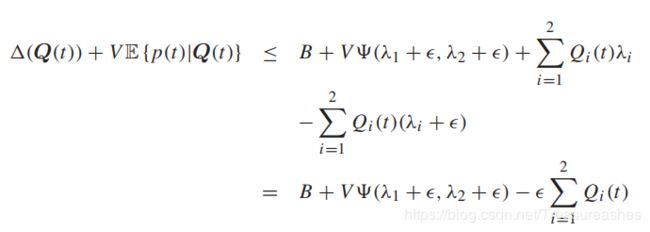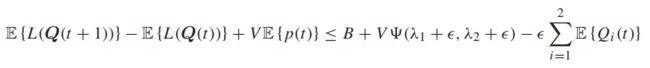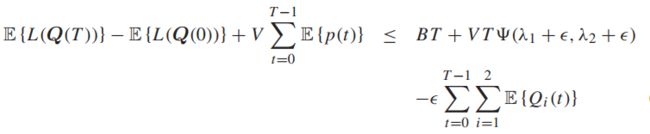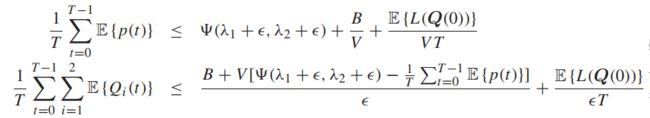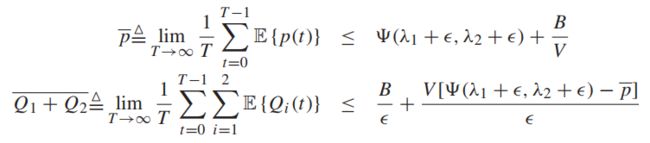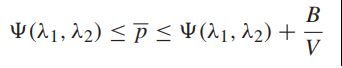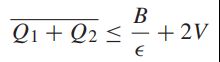【随机优化】李雅普诺夫优化在通信与排队系统中的应用（第三章）-动态规划示例

【参考书目】Stochastic Network Optimization with Application to Communication and Queueing Systems

【作者】（美）Michael J.Neely---University of Southern California

【出版社】MORGAN&CLAYPOOL PUBLISHERS

目录

稳定调度

S-ONLY算法和e最大

​

网络容量区（network capacity region）

用于稳定调度的李雅普诺夫漂移

“最小漂移（MIN-DRIFT）”或“最大权重（MAX-WEIGHT）”算法

迭代期望和伸缩和

稳定性和平均功率最小化

漂移加惩罚（DRIFT-PLUS-PENALTY）

漂移加惩罚（DRIFT-PLUS-PENALTY）算法的分析

最优化边界

问题的泛化

---

【优点】

漂移最小化方法使用当前信道状态和当前队列积压来稳定系统，并且不需要业务速率或信道概率的先验知识。

【系统模型】同第一章第二章

 

稳定调度

【假设】

-----到达向量：是独立同分布的，且为包的整数单元

 

,-----到达率定义

,-----第二瞬间（the second moments）的定义，是有限的

 

 

 

-----信道向量：信道是时变的

-----被转移的包的数量（非负）

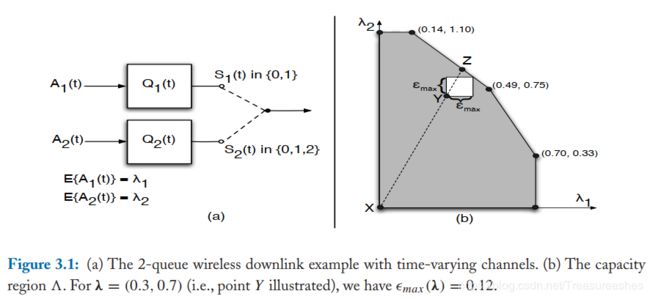
信道状态S1(t)与S2(t)是独立同分布的：

-----传输决策，有三个可能的值：

对应的动态等式：

-----提供服务的数量

 

S-ONLY算法和e最大

-----信道中六个可能的输出结果

S-ONLY调度算法仅基于观测到的S(t)作出决策，也可能通过观察S(t)的概率来作出决策。

-----S-ONLY调度算法下的传输决策

-----在此种策略下最终的传输率，独立同分布

对于每一个时隙：

转存失败重新上传取消-----

只有满足：时队列1速率稳定

对于有限延迟，需要将传输速率设计为严格大于到达速率。

【问题规划】

 

8个作为上述线性规划的限制的已知参数：

13个作为上述线性规划的优化变量的未知参数：

 

网络容量区（network capacity region）

-----速率向量

----表示速率向量之间距离的度量

-----满足的所有非负的速率向量的集合

在网络容量区的S-ONLY调度算法

用于稳定调度的李雅普诺夫漂移

只要到达率向量在容量区域内部，它就提供了强稳定性。我们只需要证明满足上式的S - only算法的存在，而不需要求解该S - only算法定义中的13个变量。

-----当前队列积压向量

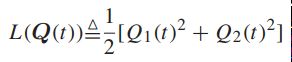-----李雅普诺夫函数，网络中队列拥塞的度量，具有如下性质：

• 当且仅当时隙t网络为空时它为0
• 它是小的说明两个队列的积压都小
• 它是大的说明至少有一个队列积压比较大

-----为什么利用二次项：拥有优势交叉项，包括排队积压和传输速率的内积

我们需要将Lyapunov函数持续推向低拥塞区域，先计算一个时隙中Lyapunov函数变化的界限：

如果对于任意值都成立：

则有：

定义在时隙t下带条件的李雅普诺夫漂移：。式中的期望取决与控制策略，并与随机信道的状态和所做的（可能随机的）传输决策有关。

更常见的控制策略应该满足：

到达都是独立同分布的，即当前的队列积压都是独立的，所以有：

对于所有可能的Q(t)及所有可能采取的决策，第一项会小于一个常数：

对于当前的系统模型，可以直接计算出来：

所以B可以定义为：

所以得到：

为了强调转移决策的重要性，将式子化为：

 

“最小漂移（MIN-DRIFT）”或“最大权重（MAX-WEIGHT）”算法

为了做出最好的转移决策来最小化漂移边界，因为它只影响到右边的最后一项，所以将问题转化为最大化：

利用机会地最大化期望的概念，将上述问题转化为最大化（最大权重算法）：

对于只有三种决策的系统，对于每一个选项，很容易衡量出权重的总值：

最大权重算法选择在信道I上以Qi(t)Si(t)的最大(正)值进行传输，如果两个信道的该值都为0，则该算法保持空闲。

因为这个算法最大化权重总和，我们有：

-----任何可能在时隙t做出的传输决策（可能是随机的）

固定一个决策去比较，并取上述不等式的条件期望(给定Q(t))将会服从：

将上式直接插入上节最后的那个式子，得到：

整理一下：

-----代表当转移决策做出后，所有信道可能提供的转移率

假定到达率在容量区域之内，并且考虑特定的转移决策可以选择了一个选项独立于队列积压，并服从于网络容量那节最后一个式子。因为信道状态是独立同分布的，并且转移率是独立于当前的信道状态。我们可以得到：

将此式插入上式，可得：

且其与线性规划问题相关，但我们不用解出来，只要知道这个线性规划问题的解存在即可。

 

迭代期望和伸缩和

将上式在随机的值上取期望：

带入定义式，得：

替换式子的左边：

利用伸缩和将各个时隙的值累加上：

将最大项分开，并利用，得到：

假设，取一个极限的超量：

因此，只要速率向量在网络容量区域内，所有的队列都是强稳定的，并且所有的队列积压小于右边。平均队列拥塞界限与速率向量离开容量区域边界的距离成反比。

-----可以代替上式中的极限的超量：平均时间的队列积压

等待时间也可以根据利特尔定理计算出来：

实际的最大权重算法的性能比界限所建议的要好得多，可能的三个原因：

• 在计算Lyapunov漂移时使用了一个简单的上限
•  B值在服务的第二时刻使用了一个上限
• 漂移不等式与不知道队列的S - only算法相比，而实际漂移要好得多，因为我们的算法考虑了队列积压

第三个原因通常在有很多队列的网络中占主导地位。例：如果使用不知道队列的算法，在具有一个服务器和开/关信道的N队列无线系统中的平均拥塞和延迟至少与N成比例

 

稳定性和平均功率最小化

系统模型同上

-----因为转移决策而产生的功率消耗

-----功率消耗是转移决策的函数

-----简单的函数示例

-----对于容量区域给定的速率向量，使用S-only算法使得所有队列稳定的最小的平均功率消耗，可以通过解以下线性规划问题得出：

可以看出：

是可以稳定系统的任何的控制策略（不论是不是S-only）下的最小平均功率消耗；

它是连续的、凸的和入口非递减（entrywise non-decreasing）的

 

对于所有满足下式的e：

若原速率向量属于容量区域，则可得：

存在一个S-only算法使得所有的转移决策满足：

漂移加惩罚（DRIFT-PLUS-PENALTY）

当李雅普诺夫函数定义为：

则代表的是有条件的李雅普诺夫漂移。当采取措施使其界限最小化可以稳定系统，但由此产生的平均功率消耗可能会不必要的大。

相比于简单地最小化有条件的李雅普诺夫漂移的界限，我们可以最小化漂移加惩罚的界限：

-----一个参数，代表我们对功率消耗的权重

类似上一节，我们得到式子：

DRIFT-PLUS-PENALTY算法在每个时隙t都会观察与来最小化不等式的右边，与之前一样，利用机会最小化期望，我们需要贪婪地最小化下式：

然后我们观察下式，找到一个转移决策使下面的值最小化：

 

漂移加惩罚（DRIFT-PLUS-PENALTY）算法的分析

由于我们每次都最小化右边，所以可以得到：

假设速率向量从属于容量区域，固定一个符合条件的e值。注意到转移决策独立于队列积压，把S-only算法插入左边：

利用迭代的期望：

把的每个时隙的加起来：

整理一下，一个根据VT分开，一个根据eT分开：

取极限得到：

最优化边界

因为上述两式对任意小于最大值的e都满足，所以我们可以分开地优化。把它的最大值插入上式，表示两个队列都是强稳定的。再使e=0使得：

【性能界限式1】

从上式可以看出，时间平均功率消耗不可能比小，且这个下确界需要满足所有的算法都实现稳定。

因为所以

这表明至少需要一个单元的能量去支持每个新来的包，所以增加了总的输入率，同时需要的最小平均功率至少增加了2e。将上式插入上一小节的最后一个式子，得到对于每一个小于最大值的e值都满足的式子：

对于最大值，则有：

【性能界限式2】

两个性能界限式展示了[O(1/V)，O(V)]功率积压权衡：我们可以使用任意大的V来使B/V任意小，因此【性能界限式1】意味着时间平均功率p任意接近最佳值(λ1，λ2 )。这需要权衡：在【性能界限式2】中绑定的平均队列积压是O(V)。

 

仿真略过。

 

问题的泛化

2队列系统可以被一个更大的K队列的系统替换。

事实上，最小漂移（MIN-DRIFT）算法可以泛化为选择一个转移决策最大化：

 

这些对更一般的信道状态、更一般的资源分配决策、更一般的随机速率函数以及更一般的惩罚函数都支持。

特殊化的例子：

-----可以有不确定的可能的输出状态数量

-----可以有不确定的可能的功率分配，也可以代表更复杂的物理层操作，如调制、编码、波束形成等。

-----可以是把信道状态和资源分配映射到转移率的任意函数

-----惩罚函数不一定是代表功率，也可以是任意关于分配决策的任意函数