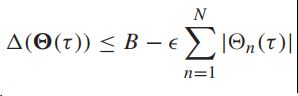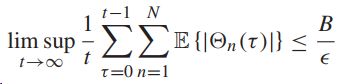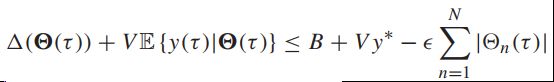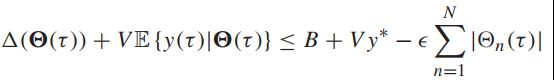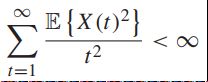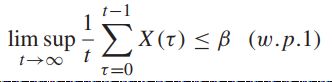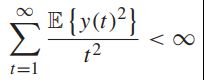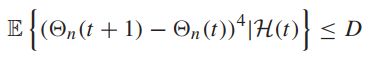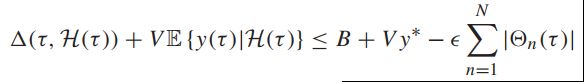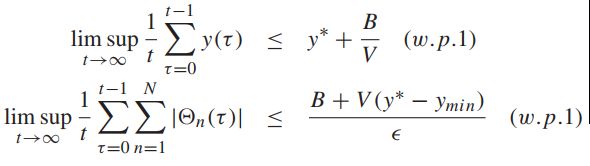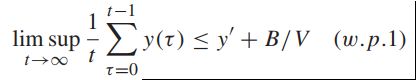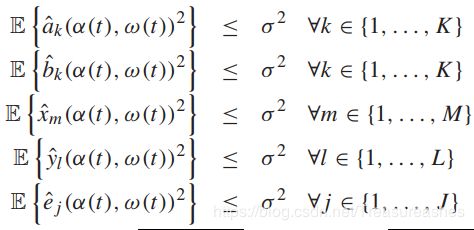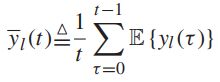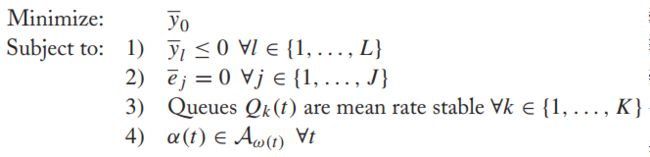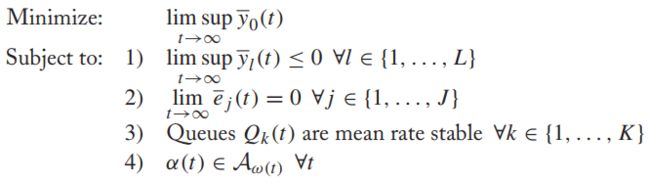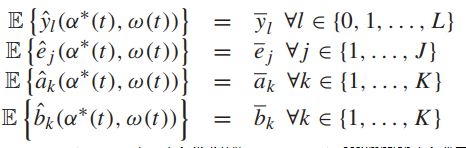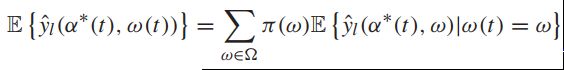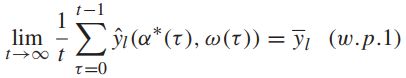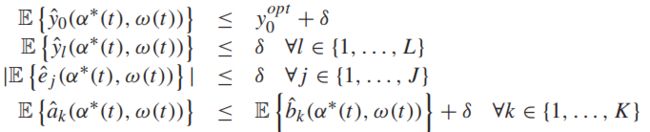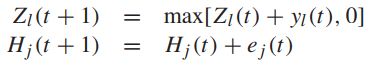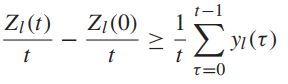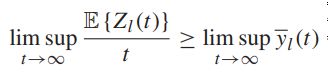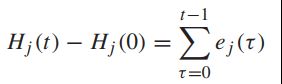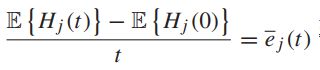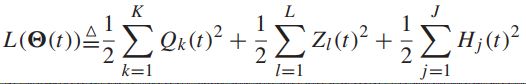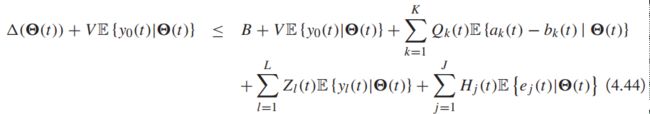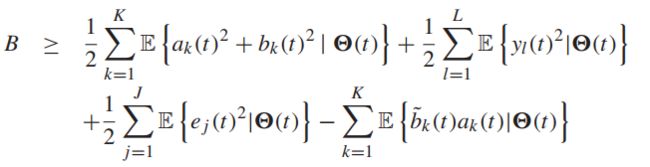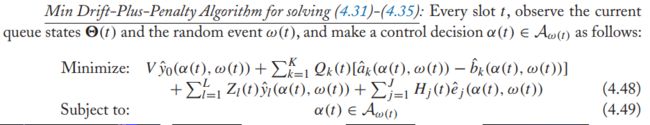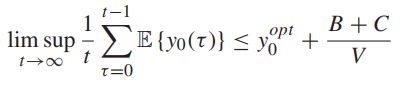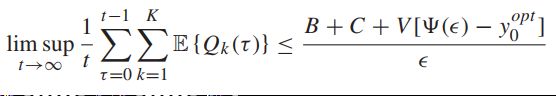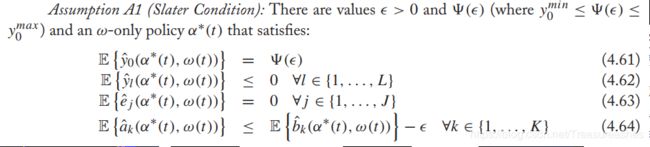【随机优化】李雅普诺夫优化在通信与排队系统中的应用(第四章)-优化时间平均
【参考书目】Stochastic Network Optimization with Application to Communication and Queueing Systems
【作者】(美)Michael J.Neely---University of Southern California
【出版社】MORGAN&CLAYPOOL PUBLISHERS
目录
李雅普诺夫漂移与李雅普诺夫优化
李雅普诺夫漂移定理
李雅普诺夫优化定理
概率为1的收敛
通常的系统模型
边界假设
基于w-only策略的优化
虚拟队列
最小化漂移加惩罚算法
李雅普诺夫漂移与李雅普诺夫优化
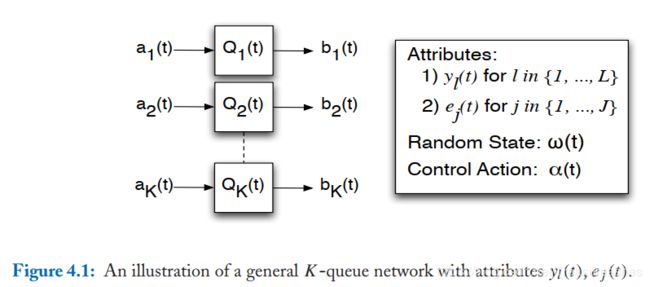
【系统模型】
N个队列
![]() -----队列的积压向量,存在一定的概率规则
-----队列的积压向量,存在一定的概率规则
![]() -----实数,且可以为负
-----实数,且可以为负
【二次的李雅普诺夫函数】
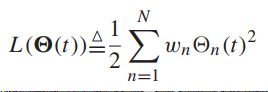 -----用于衡量积压队列的大小,通常为非负,当且仅当所有的队列积压为零时其为零
-----用于衡量积压队列的大小,通常为非负,当且仅当所有的队列积压为零时其为零
![]() -----正权重的集合,通常对于每个队列都是1,可以区别对待不同的队列
-----正权重的集合,通常对于每个队列都是1,可以区别对待不同的队列
李雅普诺夫漂移定理
【定理4.1 李雅普诺夫漂移】假定二次的李雅普诺夫函数中的![]() 且假定存在
且假定存在![]() 满足【漂移条件】:
满足【漂移条件】:
则可以得到:
如果![]() 则所有的队列是平均速率稳定的;
则所有的队列是平均速率稳定的;
如果![]() 则所有的队列是强稳定的,并且满足下式:
则所有的队列是强稳定的,并且满足下式:
-----平均队列积压上限
证明略过。
上述定理的证明揭露了考虑长时间的平均队列积压的更多的详细信息,也表明了初始条件是怎么慢慢地衰退。
李雅普诺夫优化定理
【定理4.2 李雅普诺夫优化定理】假定![]()
![]() ----常数
----常数
![]() -----对于每个时隙的积压向量的所有可能值
-----对于每个时隙的积压向量的所有可能值
因此,我们有:
则所有的队列为平均速率稳定。
![]()
![]() 时第二个式子仍然成立,
时第二个式子仍然成立,![]() 时第一个式子仍然成立。表明即使保证平均时间惩罚的结果,也仍然保持了强稳定性。
时第一个式子仍然成立。表明即使保证平均时间惩罚的结果,也仍然保持了强稳定性。
证明略过。
这个结果表明了以下的控制策略:每一个时隙,观察当前的队列积压然后做出控制决策,在知道队列积压的条件下,贪婪地最小化漂移加惩罚表达式:
如果存在一个特定的控制策略满足整个表达式:
那么贪婪地最小化漂移加惩罚的策略也会满足这整个要求。
如果V=0,那就相当于只最小化漂移,便退化为Tassiulas-Ephremides technique。
概率为1的收敛
以下,我们提供一个对于样本路径时间平均的概率为1的收敛,而不是时间平均期望。以下的先行引理与Kolmogorov law of large number有关。
【引理4.3】
假定以下成立:
![]() -----实值的常数
-----实值的常数
则可以得到:
【附加的三个假设】
![]() -----队列向量
-----队列向量
![]() -----所有的历史(full history),包括所有时隙的队列向量和惩罚过程,定义为:
-----所有的历史(full history),包括所有时隙的队列向量和惩罚过程,定义为:
在此基础上假设:
- 存在一个确定的常数,有:
所以队列变化的条件第四时刻(conditional fourth moments)拥有不一致的下界(uniformly bounded)
【定理4.4 概率收敛为1的李雅普诺夫优化】
假设![]() 为概率为1收敛的确定值,满足上述三个假设,并且有几个常数
为概率为1收敛的确定值,满足上述三个假设,并且有几个常数![]() 会满足:
会满足:
则所有的队列是速率稳定的,且满足:
更近一步,如果相同的假设满足,会存在一个y'值,使用以下的附加的不等式会对所有的时隙和可能的队列都满足:
得到:
如果对所有的历史H加上一定的条件,则需要通过引理4.3来证明定理4.4。在每个时隙贪婪地最小化
![]()
相当于贪婪地最小化
![]()
![]()
目前,我们关注之前的【李雅普优化定理】中的两个式子,如果附加的三个假设都成立的话,则他们在平均时间上具有相同的边界。
通常的系统模型
![]() -----随机过程(独立同分布)
-----随机过程(独立同分布)
![]() -----控制决策
-----控制决策
![]() -----特征向量
-----特征向量
![]() -----随机事件的静态概率分布
-----随机事件的静态概率分布
![]() -----随机事件的样本空间
-----随机事件的样本空间
如果样本空间是确定的或者可数的不确定的,那么静态概率分布代表概率批量函数(probability mass function):
如果是可数不确定的,那么它代表概率密度。
边界假设
所有的上述函数都是寻常的(非凸且不连续的),但是我们假设他们有特定的静态概率分布,并满足下面的界限:
【边界假设式】
基于w-only策略的优化
对于每一个![]() ,定义:
,定义:
【问题规划】
更精确的问题可以定义为:
【精确问题规划】
w-only策略:在每个时隙观察w(t),再独立地做出一个决策动作。
-----代表在时隙t使用w-only策略作出的所有动作
因为w(t)是静态概率分布的,所以对于每个时隙,以下式子的期望都相同:
对于以上这些性质,可以利用在每个性质上的静态概率分布来衡量其对应的权重:
在假设w(t)为一个静态概率过程之外,我们还可以作出【温和的大数定律的假设(mild"law of large number" assumption)】来考虑时间平均(不是时间平均期望):在任何满足w-only策略的每个时隙的期望![]() 的条件下,不确定的水平(horizon)时间平均
的条件下,不确定的水平(horizon)时间平均![]() 会概率1地相等于
会概率1地相等于![]() ,例如:
,例如:
【大数定律假设】
对于任何时隙,只要w(t)为独立同分布,这个假设都能成立。这是因为,根据大数定律,![]() 是在所有时隙上确定平均值为
是在所有时隙上确定平均值为![]() 的独立同分布。
的独立同分布。
这个假设对其它静态分布的更大的类也成立,如不可减的(irreducible )离散马尔可夫链。
It does not hold, for example, for degenerate stationary
processes where ω(0) can take different values according to some probability distribution, but is
then held fixed for all slots thereafter so that ω(t) = ω(0) for all t.
【定理4.5 优化的w-only策略】 假设ω(t)服从静态概率分布, 并且这个系统满足【边界假设】又满足【大数定律假设】,则在此系统上的【精确问题规划】是可用的,而且对于任意的![]() ,在任一个时隙上存在满足
,在任一个时隙上存在满足![]()
的转移决策,并且有:
虚拟队列
为了解决【精确问题规划】,我们先将所有的不等式和等式限制在队列稳定性问题上。
一般来说,虚拟队列Z存在限制![]()
对于任意一个时隙t>0,有:
取期望且使t趋近于无穷,可得:
如果Z为平均速率稳定的,那么:
至此,我们的平均时间限制已经满足了,这个问题被转化为一个单纯的队列稳定性问题。
【定理2.5】
把每个时隙的H的更新等式累加起来:
取平均并根据t来整理:
可以得到,如果H是平均速率稳定的,便等值限制也满足了:
【精确问题规划】转变为:设计一个策略,保证实际队列和虚拟队列的平均速率稳定,并且使平均时间限制与我们想要的值相同。
原始的问题便可以转化为:在保证队列稳定性的条件下,最小化损失函数时间平均。
最小化漂移加惩罚算法
【引理 4.6】假设ω(t)是独立同分布的blabla
存在下式:
这里的B对每一个时隙都满足:
相比于直接最小化![]()
我们一般会最小化【引理4.6】右边项的边界:
这种算法的突出性在于不需要知道ω(t)的概率分布,在观察了ω(t)之后,它在所有的决策里寻找一个最小的函数值。它的复杂性取决于这些函数的结构。它评估所有的选项,并在其中选一个最好的。
当![]() 是不确定的时候,上述问题可能不会有一个确定的下界。然而,比起假设我们的决策会在每一个时隙都有一个下确界(或者接近于这个下确界),我们更需要分析提出的算法在附加的下确界常数限制下实现的性能表现。
是不确定的时候,上述问题可能不会有一个确定的下界。然而,比起假设我们的决策会在每一个时隙都有一个下确界(或者接近于这个下确界),我们更需要分析提出的算法在附加的下确界常数限制下实现的性能表现。
附加C的漂移加惩罚算法(C-additive approximation of the drift-plus-penalty algorithm)是指:
在每一个时隙t和当前的队列下,选择(可能是随机地)一个动作决策满足在【引理4.6-式1】右边的一个条件期望值,这个条件期望值在从这个覆盖所有可能的控制决策的下确界而来的一个常数C内。
这个定义允许这个下确界可以生发出从期望的角度的解释,相比于一个确定性的意义,这将在一些应用中更加有用。这些附加C的优化方法可以处理过时的积压信息,和在有干扰网络中最大化吞吐量。
【定理4.8 最小化漂移加惩罚算法的性能表现】假定ω(t) 是独立同分布的,【精确的问题规划】是可用的,
![]() 有一个固定值
有一个固定值![]() 如果在每一个时隙使用附加C的漂移加惩罚算法,则有:
如果在每一个时隙使用附加C的漂移加惩罚算法,则有:
-
时间平均成本(cost)将会满足:
B为【引理4.6-式2】中的定义
-
所有的队列为平均速率稳定,并且【精确问题规划】中的限制也能满足
-
假定存在常数满足 Slater condition of Assumption A1 holds,则有:
![]() -----满足限制的常数
-----满足限制的常数
我们注意到,在( 4.50 )和( 4.51 )中给出的边界不仅仅是无限水平(infinite horizon)边界:下面证据中的不等式( 4.58 )和( 4.59 )表明,当所有初始队列积压都为零时,这些边界对所有时间t > 0都有效,如果初始队列积压非零,则必须包括像O ( 1 / t )一样衰减的“虚假因子”。上述定理适用于ω( t )是时隙上的独立同分布的情况。正如第4.9节所讨论的,相同的算法可以在更一般的遍历ω( t )过程以及非遍历过程中提供相似的性能。
【假设A1】
这个假设保证了很强的稳定性。然而,即使没有这个假设,特定的问题结构也会有一个很强的确定性(deterministic)的队列边界.
我们要在哪里用独立同分布(i.i.d)的假设?
在上述的ω-only策略对 ω(t)作出了独立同分布的假设。因为过去的值会对当前的信道状态产生影响,这个影响会改变当前的 ω(t)的分布。然而,对于上述的证明,独立同分布的假设是很重要的,但对整个系统的性能表现并不重要。