平衡二叉树之一（基本性质、查询、添加） .

平衡二叉树（Balanced BinaryTree）又被称为AVL树。它具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

一、平衡二叉树的基本性质

根据二叉树的性质高度为h的AVL树，节点数N最多为2^h-1；其最少节点树为(((1 + √5) / 2) ^h+2 - ((1 - √5) / 2)^h+2)/ √5 - 1。
最少节点数n的形式化证明如下：

• 假设N_h-1表示高度为h-1的具有最少节点数的平衡二叉树的节点总数，即少任意一个节点都无法组成一个平衡二叉树
• 假设N_h-2表示高度为h-2的具有最少节点数的平衡二叉树的节点总数，即少任意一个节点都无法组成一个平衡二叉树
• 则根据平衡二叉树的性质，为了构造高度为h的具有最少节点的平衡二叉树
  • 它的两棵子树的高度差的绝对值为1，即两棵子树一棵高度为h-1，一棵高度为h-2
  • 两棵子树都具有最少的节点数
• 因而可得N_h = N_h-1 + N_h-2 + 1 

而且很显然N₀ =0，N_{1 =1，而斐波那契数列为}F_n= F_n-1 + F_{n-2，其序列形式为0,1,1,2,3,5...。用数学归纳法很容易证明Nh = Fh + 2- 1，再根据斐波那契数列的值可得高度为h的平衡二叉树的最少节点数为Fh + 2 - 1 =(((1 + √5) / 2) ^h+2 - ((1 - √5) / 2) ^h+2)/ √5 - 1 。}由于-1 < (1-√5)/2 < 0，所以:

((1 + √5)/2)^h+2=√5 * (N_h  + 1 )  + ((1 - √5) / 2)^h+2 < √5 * (N_h  + 1 ) + 1

h < log(√5 * (N_h  + 1 ) + 1) / log((1 + √5)/2) - 2 < 1.5 * log(√5 * (N_h  + 1 ) + 1) - 2 < 1.5 * log(√5 * (N_h  + 2 )) - 2 < 1.5 * 1.16 + 1.5 * log(N_h  + 2)  - 2 < 1.5 * log(N_h  + 2)

因此其高度为O(logn)，可以得到很好的添加、删除、查询效率。在平衡二叉树上的插入、删除、以及查询操作不需要额外的空间。

平衡二叉树一般是一个有序树，它具有二叉树的所有性质，其遍历操作和二叉树的遍历操作相同。但是由于其对二叉树施加了额外限制，因而其添加、删除操作都必须保证平衡二叉树的性子被保持。

平衡二叉树中引入了一个概念：平衡二叉树节点的平衡因子，它指的是该节点的两个子树，即左子树和右子树的高度差，即用左子树的高度减去右子树的高度，如果该节点的某个子树不存在，则该子树的高度为0。

二、平衡二叉树的查询

在有序平衡二叉树上的查询操作非常简单，基本算法为：

1. 和当前节点比较，如果相等则结束
2. 否则根据和当前节点比较的结果查询当前节点的左子树或者右子树（如果下一步要查找的子树不存在，则查询结束，不存在要查找的节点）

因此平衡二叉树的查询操作的效率取决于平衡二叉树的高度，即O(logn)。

三、平衡二叉树的添加

平衡二叉树的添加操作是比较复杂的，因为添加后，平衡二叉树的平衡性质可能要被打破，此时就要对树进行调整以保证平衡二叉树的性质被保持住。平衡二叉树的插入操作基本分为以下两部步：

1. 插入：这个操作很容易立即，就是要插入节点，该操作就是找到插入点并把节点插入到树中
2. 根据高度变化进行调整：很明显插入一个节点（假设为new），至少会影响以插入节点的父节点（假设为p）为根节点的树的高度，根据树高度的定义，可以知道这又会进一步影响到以从”树的根节点（假设为root）到p的路径上的所有节点“为根节点的子树的高度。另一方面，如果new被插入到节点a的子树中，但是该节点的高度在new被插入后并没有变化，则以从”root到a的路径上的所有节点“为根的子树的高度也不会变化。因而在new被插入后，只需要沿着”树的根节点（假设为root）到p的路径“的反向路径依次处理各个节点，找到第一个高度不满足平衡二叉树要求的节点，然后对其进行调整，使其高度不再发生变化。

插入操作通常很简单，就是找到插入点，然后将新的节点插入到树中。

在平衡二叉树的插入中，最繁琐的、最难的就是在找到某个节点，以该节点为根节点的子树不满足平衡二叉树的要求，使得调整后的以该节点为根节点的子树满足平衡二叉树的要求。树的调整分以下几种情况（假设以a为根节点的子树在插入新节点后不满足平衡二叉树的要求了）：

2.1 LL型

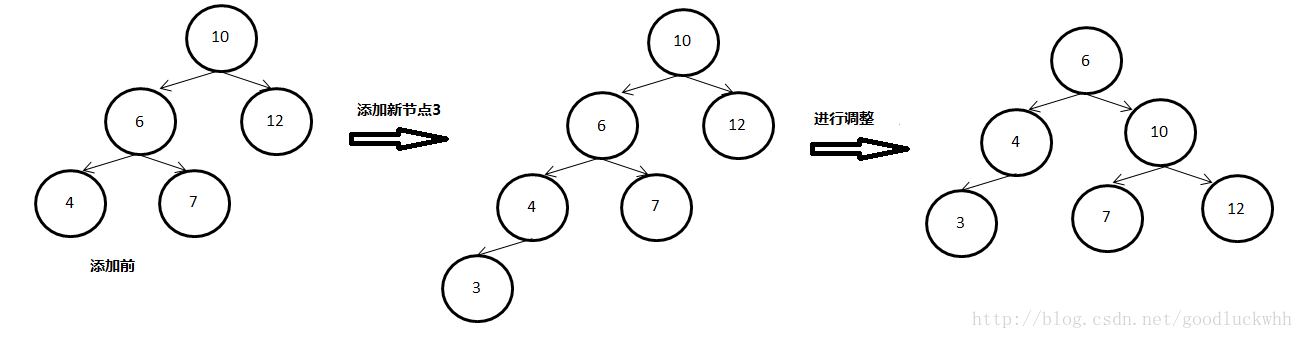
LL型指的是由于在a的左子树的根节点的左子树上添加了节点而导致a的平衡因子从1变成了2。这时需要对树进行一次调整使得平衡二叉树的要求得以满足，这个操作通常称为左旋。如图所示

在调整后，还需要相应的更新调整操作涉及到的节点的平衡因子，同时还要分析下调整对以各个节点为根节点的子树的高度的影响。以上图为例，假设添加新节点前节点10,6,12,4,7的高度分别为h1,h2,h3,h4,h5，则在添加前：

1. 由于添加新节点前以节点10为根节点的子树的高度为1，因而h2 = h3 + 1，h1=h2+1
2. 由于新节点被添加在节点6的左子树，并且添加新节点后以节点6为根的子树的高度增高，所以添加新节点前节点6的平衡因子为0，h4=h5，h2=h4+1

在添加完一个节点后，按照前边的分析会沿着”树的根节点（假设为root）到p的路径“的反向路径依次处理各个节点，直到找到了一个由于添加动作而导致其左右子树高度差不满足平衡二叉树的节点（在该例子中即为节点10），然后对以该节点为根的子树进行调整。在找到该节点之前对其它节点的处理比较简单，具体的过程是依据如下几个参数：

• 插入到本节点的哪个子树
• 被插入到的子树的高度是否改变
• 该节点的原有平衡因子

来决定以该节点为根的子树的高度是否改变，以及该节点的新的平衡因子。简单的算法描述如下（以插入到左子树为例，插入到右子树的情形与它对称）：

1. 如果插入到该节点的左子树但左子树高度不变，则该节点的平衡因子不变，以该节点为根节点的子树的高度不变，否则
2. 如果插入到该节点的左子树且左子树高度增高，则：

• • 如果该节点原有平衡因子为1，则需要进行调整
  • 如果该节点原有平衡因子为0，则以该节点为根节点的子树的高度增高，该节点的新的平衡因子为1
  • 如果该节点的原有平衡因子为-1，则以该节点为根节点的子树的高度不变，该节点的新的平衡因子为0

在经过上述的处理并找到以其为根节点的不满足平衡二叉树要求的节点后（上图中即为节点10），除了该节点外，其它节点的信息都已经根据插入的节点做了相应的更新。现在需要对以该节点为根的子树进行调整以使得新得到的树是一棵平衡二叉树。此时关键在于分析调整对节点平衡因子的影响，以及对以其为根节点的子树的高度的影响。

以上图为例，很显然参与调整的节点包括节点6,7,12，因而只需要分析这三个几点即可。在调整后，节点6替换了节点10的位置（指的是称为了节点10的父节点的子节点），只要它的高度与原来处于该位置的节点10的高度相比不发生变化，则添加新节点对原树高度的影响到此就结束了。

1.    先分析节点6的左子树，即节点4。很明显该调整不影响其左右子树，因而其平衡因子以及以其为根的子树的高度在调整前后不发生变化。但是需要注意的是以几点4为根节点的子树的高度在添加完新节点后变成了h4 + 1。

2.    再分析节点6的右子树，即节点10的情形。由于该节点的左孩子发生了变化，因而需要进一步分析其左孩子的变化（即节点7的变化），以及其新的左右子树的高度差。

• 很明显该调整不影响节点7的左右子树，因而其平衡因子以及以其为根的子树的高度在调整前后不发生变化。以节点其为根节点的子树在插入新节点前后高度也没有发生变化，仍为h5。

由于节点10的右子树在插入前后以及调整前后都没有发生任何变化，因而节点12的平衡因子不变，以其为根节点的子树的高度仍为h3。则调整后节点10的新的平衡因子为（h5 - h3） = h2 -1 - （h2 - 1）= 0。以节点10为根节点的子树的高度为h3 + 1 = h2

3.    则调整后节点6的新的平衡因子为 h4 + 1 - h2 = 0，以节点6为根节点的子树的高度为h2 + 1，与原来处于该位置的节点10的高度相同，因而在调整完毕后插入即可结束

从上述分析可以看出，对于该种类型的调整，在调整完后，仅需要修改节点6和节点10的平衡因子为0即可。

2.2  RR型

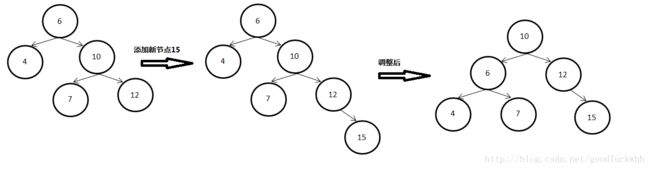
RR型指的是由于在a的右子树的根节点的右子树上添加了节点而导致a的平衡因子从-1变成了-2。此时只需要一次向左的旋转操作即可。如图所示

该类型实际上是和LL型对称的，因而不再具体分析。

2.3 LR型

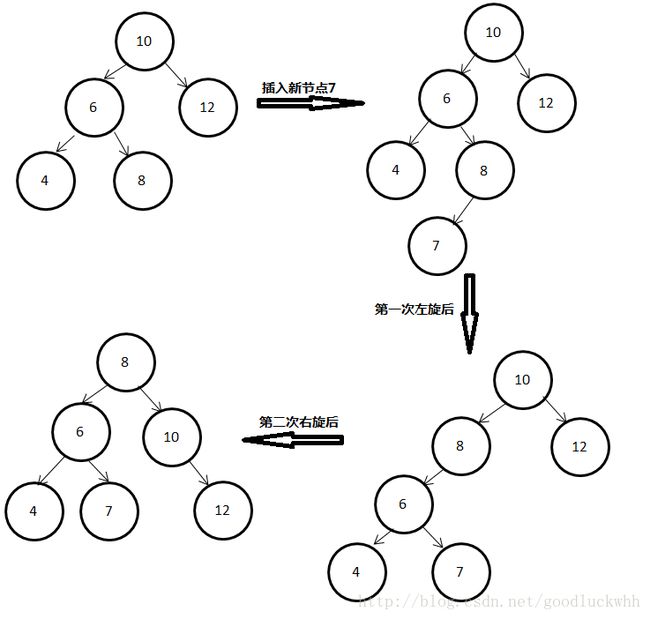
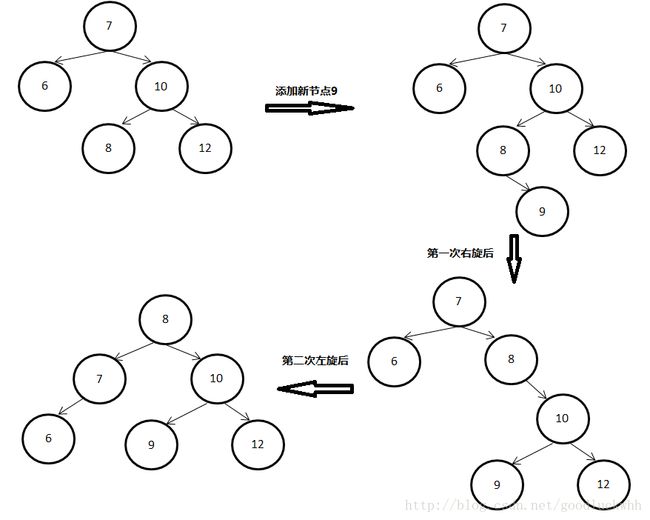
LR型指的是由于在a的左子树的根节点的右子树上添加了节点而导致a的平衡因子从1变成了2。此时需要两次旋转操作，先左旋后右旋。

在该种类型中假设找到的以其为根节点的子树不满足平衡二叉树要求的节点为x，x的左子树的根节点为y，y的右子树的根节点为z，则x，y，z以及z的左（右）孩子都需要参与调整，因而根据z在插入节点后的平衡因子的三种情形分别进行处理，这三种情形分别为（在找到x节点时）：

• z的平衡因子为0
• z的平衡因子为1
• z的平衡因子为-1

上图中的情形对应于z的平衡因子为-1的情形。具体的分析过程可以参考LL型的分析过程。调整后的最终结果：

• 节点z处于节点x原来的位置（指的是称为了节点x的父节点的子节点），以节点z为根节点的子树的高度等于插入前以节点x为根节点的子树的高度，节点z的平衡因子为0
• 节点x的新的平衡因子为0
• 节点y的新的平衡因子为1

下图对应z的平衡因子为1的情形：

调整后的最终结果：

• 节点z处于节点x原来的位置（指的是称为了节点x的父节点的子节点），以节点z为根节点的子树的高度等于插入前以节点x为根节点的子树的高度，节点z的平衡因子为0
• 节点x的新的平衡因子为-1
• 节点y的新的平衡因子为0

下图对应z的平衡因子为0的情形：

调整后的最终结果：

• 节点z处于节点x原来的位置（指的是称为了节点x的父节点的子节点），以节点z为根节点的子树的高度等于插入前以节点x为根节点的子树的高度，节点z的平衡因子为0
• 节点x的新的平衡因子为0
• 节点y的新的平衡因子为0

2.4 RL型

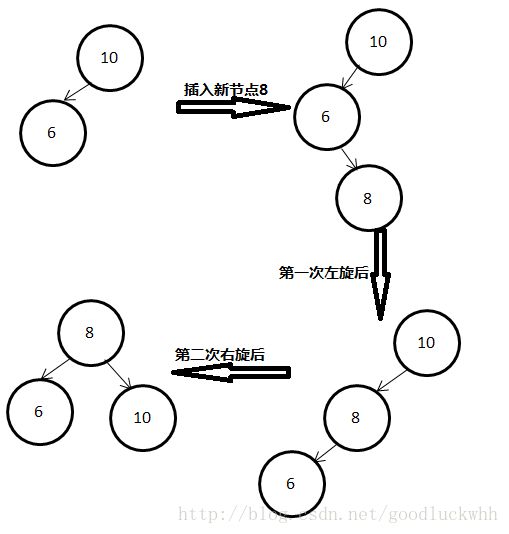
RL型指的是由于在a的右子树的根节点的左子树上添加了节点而导致a的平衡因子从-1变成了-2。此时需要两次旋转操作，先右旋后左旋。

RL型与LR型是对称的，也分三种情形。

因此平衡二叉树的插入分为两步，第一步找到插入点，时间复杂度为O(logn)，第二步找到需要调整的子树进行最多两次调整，时间复杂度也为O(logn)，因而它的插入操作的时间复杂度为O(logn)。

 

http://blog.csdn.net/goodluckwhh/article/details/11693451