gm/Id 设计方法
gm/Id方法的原理
关于gm/id设计方法的原理请看Stanford ee214b的课件。这两篇对基本原理已经讲的很详细,再次不过多阐述。本篇博客主要讲如何使用gm/Id方法。
简单概括gm/Id方法的本质就是:
- gm/Id对应Vov,通过其数值大小的选取来达到增益与带宽的折衷;
- gm/Id方法是一种loop-up table方法;
- gm/Id方法为短沟道器件电路设计提供了比公式手算更准确的初值;
- gm/Id方法为亚阈值设计提供了有力的工具。
原始数据准备
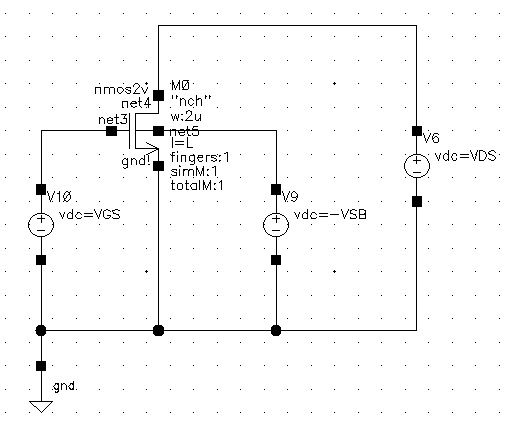
首先要在cadence或者hspice中通过大量参数扫描得到不同工作点下晶体管的小信号参数模型。此处以在cadence中得到tsmc180管子参数为例。
因为需要大量的仿真,并且导出的数据也很多,这里我们用ocean脚本来代替繁琐的操作。
注意:对于不会使用ocean语言的,可以通过这篇介绍 来快速的生成一个粗糙但不影响使用的ocean文件。
我的ocean代码如下:
simulator( 'spectre )
design( "/home/liuheng/simulation/NMOS2V_DC/spectre/schematic/netlist/netlist")
resultsDir( "/home/liuheng/simulation/NMOS2V_DC/spectre/schematic" )
modelFile(
'("/eda/library/TSMC/tsmc18rfOA/tsmc18/../models/spectre/cr018gpii_v1d0.scs" "stat_noise")
。。。此处还有很多model,能自动生成,此处为了不影响博客的视觉效果删除了一些语句。
)
analysis('dc ?saveOppoint t )
desVar( "L" 180n )
desVar( "VDS" 0.9 )
desVar( "VGS" 0.9 )
desVar( "VSB" 0 )
envOption(
'analysisOrder list("dc")
)
temp( 27 )
L_list = list(1.8e-07 2e-07 2.2e-07 2.4e-07 2.6e-07 2.8e-07 3e-07 3.2e-07 3.4e-07 3.6e-07 3.8e-07 4e-07 4.2e-07 4.4e-07 4.6e-07 4.8e-07 5e-07 5e-07 6e-07 7e-07 8e-07 9e-07 1e-06)
VGS_list = list(0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8)
VDS_list = list(0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8)
paramAnalysis("L" ?values L_list
paramAnalysis("VGS" ?values VGS_list
paramAnalysis("VDS" ?values VDS_list
)))
paramRun()
para = list("gm" "gmbs" "id" "gds" "vth" "cgg" "css" "cjs" "cdd" "cjd" "cgd" "cgs" "cdb" "cds")
foreach(xx para
model = pv("M0" xx ?result "dcOpInfo-info")
ocnPrint( ?output xx ?numberNotation 'scientific model )
)
数据处理
注意到我扫DC参数时也扫了VDS,导致得到的数据是3维的,不是很方便使用。
其实VDS变化带来的效应就是沟道长度调制效应,在模型方程中的体现就是 λ \lambda λ, 在小信号模型中的表现就是 r o r_o ro,其实我们大概推导以下公式就会发现:
g m I d = 2 μ C o x W / L I d ( 1 + λ V D S ) \frac{g_m}{I_d} = \sqrt{\frac{2\mu C_{ox} W/L}{I_d}(1+\lambda V_{DS})} Idgm=Id2μCoxW/L(1+λVDS)
因为 λ \lambda λ 的数量级为 1 0 − 3 10^{-3} 10−3, 所以 λ V D S \lambda V_{DS} λVDS 这一项可以忽略,只需要取
\[
V_{DS} = \frac{V_{DD}}{2}
\]
这样并不会带来很大的影响。
需要得到的参数
- transconductance efficiency g m I d \frac{g_m}{I_d} Idgm
- normalized current I d W / L \frac{I_d}{W/L} W/LId
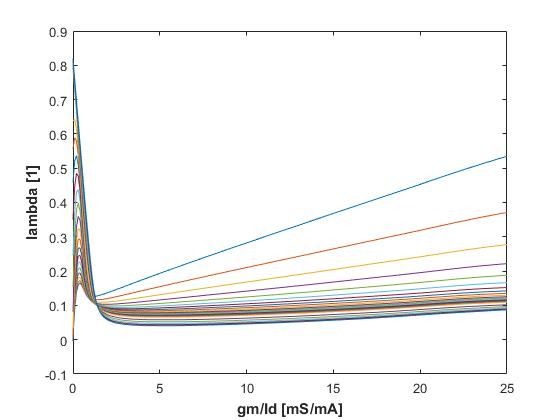
- channel length modulation factor λ = g d s I d \lambda = \frac{g_{ds}}{I_d} λ=Idgds
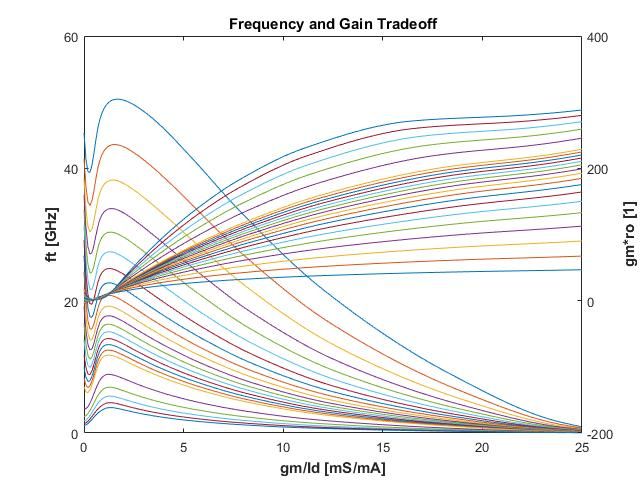
- transit frequency f t = g m 2 π c g g ft = \frac{g_m}{2\pi cgg} ft=2πcgggm
- intrinsic gain g m r o g_mr_o gmro
图中可以清楚的看出:
- gm/Id 与 Vov的对应关系;
- 通过取gm/Id的值来得到带宽与增益的折衷;
- Id/(W/L)是归一化的数据。
到目前为止就的到了我们设计电路所需要的数据,供以后查表使用。
注意:我们扫描VGS的变化是均匀的,但其实得到的gm/Id的值并不是在0-25之间均匀分布,所以我又对数据做了插值处理(但因为对这部分算法不是很熟悉,导致数据在两端外推时有不收敛的情况,从上面的图中就可以看出来曲线两头的数据应该是不太准确的。)
另外,在MATLAB中有一个built-in的函数是find(), 通过这个函数可以直接查找到曲线上对应点的准确值,这样会比从图中读曲线的值准确的多。
我的MATLAB代码 在此以供参考交流。(代码风格不是很好请见谅,希望能帮助到有需要的人)
2019年5月2日更新:因为这个matlab代码是很久以前写的了,后来有人反映可能中间有语法错误的地方。但是我后来发现其实gm/id的思想运用到设计电路中时其实不太需要经常去查表,所以代码也没有更新过,这里只是贴出我之前的工程文档,仅供思路上的参考。
另外UCBL的大神Elon有专门的matlab gmid插件,也可以参考一下。
链接:https://pan.baidu.com/s/1CFL_NRk5Ys19GD799_CRoQ 密码:ijb9
链接:https://pan.baidu.com/s/18lCfymGbb97bMVqssxMMkQ 密码:x0d7
设计实例
具体电路设计中的使用请看下面的设计实例(更新中)
Jespers
gmid方法提出者Jespers出的书以及论文.
Current Mirror OpAmp
这是一篇设计电流镜运放的报告,我用tsmc180的库基本复制出了报告中的结果。
TIA
这是博主自己高等模集跨阻放大器的设计报告,如对文中分析有不同意见的欢迎与博主讨论。
Fully Differential Folded Cascode OpAmp
这是一篇全差分折叠共源共栅运放的设计报告,还未验证。
Three-stage OpAmp
Miller OpAmp
这是两篇运放的设计报告。
Report from EE214
这是伯克利ee214课件中的两个全差分设计报告,其中第二个设计实例提供了使用优化算法寻找最佳电路参数的思路,值得借鉴。