《商务与经济统计》学习笔记（七）—各统计分布知识点归纳

阅读之前看这里：博主是正在学习数据分析的一员，博客记录的是在学习过程中一些总结，也希望和大家一起进步，在记录之时，未免存在很多疏漏和不全，如有问题，还请私聊博主指正。
博客地址：天阑之蓝的博客，学习过程中不免有困难和迷茫，希望大家都能在这学习的过程中肯定自己，超越自己，最终创造自己。

1.几何分布

在概率论和统计学中，几何分布（英语：Geometric distribution）指的是以下两种离散型概率分布中的一种：

• 在伯努利试验中，得到一次成功所需要的试验次数$X$。$X$的值域是{ 1, 2, 3, … }
• 在得到第一次成功之前所经历的失败次数$Y=X-1$。$Y$的值域是{ 0, 1, 2, 3, … }

几何分布试验的条件：

1. 试验由一系列相同的n个实验组成。
2. 每次实验有两种可能结果。我们把其中一个称之为成功，另一个称之为失败。
3. 每次实验成功的概率都是相同的，用$p$来表示；失败的概率为$1-p$。
4. 试验是相互独立的。
5. 你主要感兴趣的是，为了取得第一次成功需要进行多少次试验。

实际使用中指的是哪一个取决于惯例和使用方便。

这两种分布不应该混淆。前一种形式（$X$的分布）经常被称作shifted geometric distribution；但是，为了避免歧义，最好明确地说明取值范围。

与二项分布关心的“n次实验成功x次的概率”不同，几何分布关心的是，事件发生（或者实验）n次中，在第x次取得成功的概率。其发生的概率P为
$$f(x)=P(X=x)=(1-p{)}^{x-1}p,其中k=1,2,3,....$$

上式描述的是取得一次成功所需要的试验次数。而另一种形式，也就是第一次成功之前所失败的次数，可以写为:
$$f(x)=P(Y=x)=(1-p{)}^{x}p,其中k=0,1,2,3,....$$

记号:
若随机变量$X$服从参数为$p$的几何分布，则记为 $X\sim G(p)$
均值和方差：
$$E(x)=\mu =\frac{1}{p}$$
$$Var(x)={\sigma }^2=\frac{1-p}{p^2}$$
用途:
在重复多次的伯努利试验中，试验进行到某种结果出现第一次为止，此时的试验总次数服从几何分布，如：射击，首次击中目标时的次数。

举例：一位滑雪者不出意外顺利滑至坡底的概率是0.4，那么问
1.前10次滑雪失败，第11次成功的概率
2.第4次或不足4次就滑雪成功的概率
3.4次以上才能获得成功的概率

解答：
1.前10次滑雪失败，第11次成功的概率
$$P(X=11)=(1-p{)}^{x-1}p=q^{10}\times p=0.00241$$

2.第4次或不足4次就滑雪成功的概率
$$P(X⩽4)=1-q^4=0.8704$$

3.4次以上才能获得成功的概率
$$P(X>4)=q^4=0.1296$$

2.二项分布(伯努利分布)

二项分布是在给定每次试验的成功概率$p$、实验次数$n$的情况下，成功数$x$的频数分布。
根据$x$、$n$和$p$值的不同，二项分布也构成了一个分布家族。
在二项分布中，我们关注的是在$n$次试验中成功出现的次数。
二项分布概率函数：
$$f(x)=\left(\genfrac{}{}{0ex}{}{n}{x}\right)p^x(1-p{)}^{(n-x)}$$
$$\left(\genfrac{}{}{0ex}{}{n}{x}\right)=\frac{n!}{x!(n-x)!}$$
二项分布的数学期望和方差：
$$E(x)=\mu =np$$
$$Var(x)={\sigma }^2=np(1-p)$$

二项试验的性质：

1. 试验由一系列相同的n个实验组成。
2. 每次实验有两种可能结果。我们把其中一个称之为成功，另一个称之为失败。
3. 每次实验成功的概率都是相同的，用$p$来表示；失败的概率为$1-p$。
4. 试验是相互独立的。

伯努利分布是二项分布在n=1时的特例。一次随机试验，成功概率为$p$，失败概率为$q=1-p$，所以成功的次数也只有0和1两种情况。
其概率密度函数为：
$$f(x)=p^x(1-p{)}^{(1-x)}=\{\begin{array}{ll}p,& \text{if }\text{ x=1}\\ q,& \text{if }\text{ x=0}\end{array}$$
期望和方差：
$$E(x)=\mu =p$$
$$Var(x)={\sigma }^2=p(1-p)=pq$$

二项分布的应用举例：
如果链接点击转换为购买的概率是0.02，那么观测到200 次点击但没有购买的概率是多少？

解答

• 由于是求200次中没有成功的概率，即为1 - 200次中成功1次的概率，所以服从二项分布。
• $p=0.02$，$n=200$,$x=1$
• 代入公式得
  $$f(x)=\left(\genfrac{}{}{0ex}{}{n}{x}\right)p^x(1-p{)}^{(n-x)}=(\genfrac{}{}{0ex}{}{200}{1})0.02(1-0.02{)}^{(200-1)}$$
• 所以观测到200 次点击但没有购买的概率是
  $$P(观测到200次点击但没有购买)=1-\left(\genfrac{}{}{0ex}{}{200}{1}\right)0.02(1-0.02{)}^{(200-1)}$$

3.泊松分布

定义：单位时间内或单位空间中事件数量的频数分布
例如：我们感兴趣的随机变量可能是一小时到达洗车房的汽车数，10英里长的高速路上需要维修的路段数目。

泊松试验的性质：
1.在任意两个相等长度的区间上，事件发生的概率相等。
2.事件在某一区间上是否发生与事件在其它区间是否发生是独立的。

泊松概率函数： $$f(x)=\frac{{\mu }^x{e}^{-\mu }}{x!}$$
式中，$f(x)$为事件在一个区间发生x次的概率；$\mu$为事件在一个区间发生次数的数学期望或均值；

例题：

假定感兴趣的是工作日早上15min内到达某银行出纳窗口的汽车数量。若假设在任意两个相等长度的时间段上汽车到达的概率是相等的，并且在任意时间段上是否有汽车到达与其他事件段上是否有汽车到达是相互独立的。历史数据显示，15min内到达车辆平均数目为10。问：15min内恰好到达5辆车的概率？

解答：
$$f(x)=\frac{10^x{e}^{-10}}{x!}$$
所以$x=5$即在15分钟内恰有5辆车到达的概率为：
$$f(5)=\frac{10^5{e}^{-10}}{5!}=0.0378$$

同样的，不仅仅是15min适用，其它任意时间段也适用。现在我们要计算3min内有1辆车到达的概率是多少？

• 15min到达10辆车，所以1min到达车辆的期望值为10/15=2/3.
• 3min到达车辆数为3 $\times$ 2/3 = 2.
• 所以这时的$\mu =2$.
• 带入公式
  $$f(x)=\frac{{\mu }^x{e}^{-\mu }}{x!}$$
• 最后得到3min内有1辆车到达的概率
  $$f(1)=\frac{2^1{e}^{-2}}{1!}=0.2707$$

4.指数分布

定义：指数分布可以建模各次事件之间的时间分布情况，例如，网站访问的时间间隔，汽车抵达
收费站的时间间隔。在工程领域，指数分布可用于故障时间的建模；在过程管理领域，指数分布可用于对每次服务电话所需的时间进行建模。

指数分布概率密度函数： $$f(x)=\frac{1}{\mu }{e}^{-x/\mu }$$ 式中，$\mu$为数学期望或均值；

例题：假定在某码头装载一辆卡车所需要时间$x$服从指数分布，如果装车时间的均值或平均时间所需要时间是15分钟，即$\mu =15$，则装载一辆车花费6分钟或更少$P(x⩽6$)的概率是多少？

解答：

1. x服从指数分布，所以其概率密度函数为
   $$f(x)=\frac{1}{15}{e}^{-x/15}$$
2. 指数分布的累积概率（可以从泊松分布进行推导）为
   $$P(x⩽x_0)=1-e^{-x_0/\mu }$$
   所以
   $$P(x⩽6)=1-e^{-x_0/15}=1-e^{-6/15}$$

关于累积概率的一个推导：
如果下一个卡车装车时间要间隔时间 $x_0$，就等同于$x_0$之内没有任何卡车装车，所以服从泊松分布如下：
$$P(x>x_0)=P(N(x_0)=0)=\frac{{\mu }^0{e}^{-x_0/\mu }}{0!}=e^{-x_0/\mu }$$
反过来，事件在时间 t 之内发生的概率，就是1减去上面的值。
$$P(x⩽x_0)=1-P(x>x_0)=1-e^{-x_0/\mu }$$

泊松分布与指数分布之间的关系

连续型指数概率分布与离散型泊松分布是相互练习的，泊松分布描述了每一区间中事件发生的次数，指数分布描述了事件发生的时间间隔长度。

举例说明：假定在一小时中到达某一洗车处的汽车数可以用泊松分布描述，其均值为每小时10辆。泊松分布概率函数给出了每小时有$x$辆汽车到达的概率：
$$f(x)=\frac{{\mu }^x{e}^{-\mu }}{x!}=\frac{10^x{e}^{-10}}{x!}$$
由于车辆到达的平均数是每小时10辆，则两车到达的时间间隔的均值为： $$\frac{1小时}{10辆车}=0.1小时/辆$$
于是，描述两车到达时间间隔的对应的分布是指数分布，其均值为$\mu =0.1$小时/辆，从而指数概率分布为：
$$f(x)=\frac{1}{\mu }{e}^{-x/u}=\frac{1}{0.1}{e}^{-x/0.1}$$

5.均匀分布

我们这里主要讲的是连续性均匀分布，在讲之前均匀分布，我们先看一个例子：

令随机变量$x$表示某航班从芝加哥飞往纽约的飞行时间。假定飞行时间可以取区间[120，140]内的任意值。由于随机变量$x$可以在该区间内取任意值，因此$x$是一个连续性随机变量。对于区间[120，140]内的任意两个1分钟长度的子区间，飞行时间在这两个子区间的概率是相同的。由于飞行时间在每个一分钟长度的子区间是等可能的，因此随机变量$x$服从均匀概率分布。飞行时间是服从均匀分布的随机变量，它的概率密度函数为：
$$f(x)=\{\begin{array}{l}1/20,120⩽x⩽140\\ 0,其它\end{array}$$

连续型均匀分布，如果连续型随机变量$X$具有如下的概率密度函数，则称$X$服从$[a,b]$上的均匀分布,记作 $X\sim U[a,b]$

均匀概率密度函数如下：
$$f(x)=\{\begin{array}{ll}\frac{1}{b-a},& \text{if }a⩽x⩽b\\ 0,& elsewhere\end{array}$$

累积分布函数：
$$\{\begin{array}{l}0,x<a\\ \frac{x-a}{b-a},a⩽x<b\\ 1,b⩽x\end{array}$$

期望和方差：
$$E(x)=\mu =\frac{a+b}{2}$$
$$Var(x)={\sigma }^2=\frac{(b-a{)}^2}{12}$$

均匀分布具有下属意义的等可能性。若$X\sim U[a,b]$,则$X$落在$[a,b]$内任一子区间$[c,d]$上的概率：
$$P(c⩽x⩽d)=F(d)-F(c)={\int }_c^d\frac{1}{b-a}\mathrm{d}x=\frac{d-c}{b-a}$$

只与区间[c,d]的长度有关，而与它的位置无关。

均匀分布的概率密度函数和分布函数的定义和区别

概率密度函数：用于直观地描述连续性随机变量（离散型的随机变量下该函数称为分布律），表示瞬时幅值落在某指定范围内的概率，因此是幅值的函数。连续样本空间情形下的概率称为概率密度，当试验次数无限增加，直方图趋近于光滑曲线，曲线下包围的面积表示概率，该曲线即这次试验样本的概率密度函数。

分布函数：用于描述随机变量落在任一区间上的概率。如果将x看成数轴上的随机点的坐标，那么，分布函数$F(x)$在$x$处的函数值就表示$x$落在区间$(-\infty ，+\infty )$上的概率。分布函数也称为概率累计函数。

两者的区别：分布函数是概率密度函数从负无穷到正无穷上的积分；在坐标轴上，概率密度函数的

函数值y表示落在x点上的概率为y；分布函数的函数值y则表示x落在区间$(-\infty ，+\infty )$上的概率。

6.正态分布

正态分布（，英语：normal distribution）又名高斯分布（英语：Gaussian distribution），是一个非常常见的连续概率分布。正态分布在统计学上十分重要，经常用在自然和社会科学来代表一个不明的随机变量，比如人的身高和体重、考试成绩、科学测量、降雨量等，都近似正态分布。

概率密度函数：
正态分布的概率密度函数均值为 $\mu$方差为${\sigma }^2$(或标准差$\sigma$)是高斯函数的一个实例：

如果一个随机变量$X$服从这个分布，我们写作$X\sim N(\mu ,{\sigma }^2)$ 如果$\mu =0$并且 $\sigma =1$，这个分布被称为标准正态分布，这个分布能够简化为:

正态分布的特征：

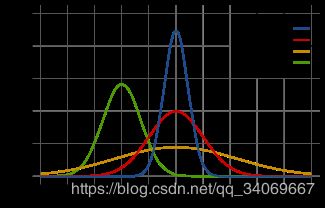
1. 正态分布族中的每个分布因均值$\mu$和标准差 $\sigma$这两个参数的不同而不同。
2. 正态曲线的最高点在均值处达到，均值还是分布的中位数和众数。
3. 分布的均值可以是任意数值：负数、零或正数。
4. 正态分布是对称的。
5. 标准差决定曲线的宽度和平坦程度。标准差越大曲线越宽、越平坦。
6. 正态随机变量的概率是由正态曲线下的面积给出。

四个不同参数集的概率密度函数（红色线代表标准正态分布）

累积分布函数：
累积分布函数是指随机变量$X$小于或等于$x$的概率，用概率密度函数表示为

正态分布的累积分布函数能够由一个叫做误差函数的特殊函数表示：

标准正态分布的累积分布函数习惯上记为$\Phi$ ，它仅仅是指$\mu =0$，$\sigma =1$时的值

将一般正态分布用误差函数表示的公式简化，可得：

它的反函数被称为反误差函数，为：

该分位数函数有时也被称为probit函数。probit函数已被证明没有初等原函数。

正态分布的分布函数$\Phi (x)$没有解析表达式，它的值可以通过数值积分、泰勒级数或者渐进序列近似得到。

上图所示的概率密度函数的累积分布函数

如何计算正态分布的概率

1.确定数据的分布
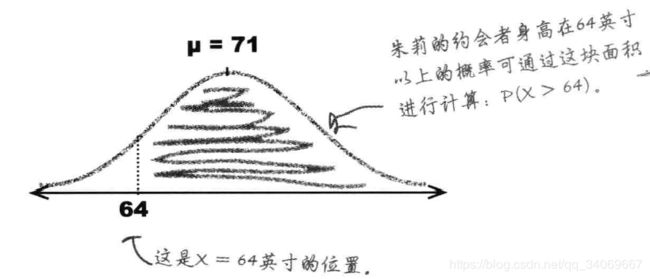
例子：朱莉已得知公司适龄男生的身高均值和标准差：均值71英寸，方差20.25.
即，如果用$X$表示男生的身高，则：
$$X\sim N(71,20.25)$$

然后我们还需要知道哪个数值范围能够得到正确的概率面积，在本例中，我们要求与朱莉(64英寸)相亲的男生具有足够高的概率。

2.转换为标准的正态随机变量
下一步是让变量X标准化，使均值为0，标准差为1，据此得出标准正态变量Z，而$Z\sim N(0,1)$
那么如何将正态分布转化为标准形式呢？
通常通过下列公式可求出任何正态变量x的标准分(关于标准分的知识可查看其它资料)：
$$z=\frac{x-\mu }{\sigma }$$

所以：
$$z=\frac{x-\mu }{\sigma }=\frac{64-71}{4.5}=-1.56$$
3.查表
通过概率表查找概率

大概我们可以找到$z$=-1.56时的概率为0.0594

正态分布的一些性质：

• 如果$X\sim N(\mu ,{\sigma }^2),$且$a$与 $b$是实数，那么$aX+b\sim N(a\mu +b,(a\sigma {)}^2)$

• 如果$X\sim N({\mu }_X,{\sigma }_X^2)$与$Y\sim N({\mu }_Y,{\sigma }_Y^2)$是统计独立的正态随机变量，那么：
  它们的和也满足正态分布$U=X+Y\sim N({\mu }_X+{\mu }_Y$, ${\sigma }_X^2+{\sigma }_Y^2)$.
  它们的差也满足正态分布$V=X-Y\sim N({\mu }_X-{\mu }_Y$, ${\sigma }_X^2+{\sigma }_Y^2)$.
  $U$与$V$两者是相互独立的。（要求X与Y的方差相等）

• 如果 $X_1$, $\cdots$, $X_n$为独立标准正态随机变量，那么 $X_1^2+\cdots +X_n^2$服从自由度为$n$的卡方分布。

博主码字不易，大家关注点个赞转发再走呗 ，您的三连是对我创作的最大支持^ - ^