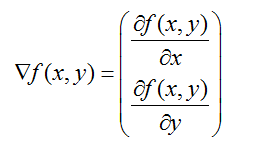实现Logistic回归

Logistic回归介绍

logistic回归是研究观察结果为二分类或多分类时，与影响因素之间关系的一种多变量分析方法，属于概率型非线性回归。它的主要是想是根据现有数据对分类边界线建立回归公式，并以此进行分类。

通过分类边界线进行分类，具体说来就是将每个测试集上的特征向量乘以回归系数(即最佳拟合参数)，再将结果求和，最后输入到logistic函数(也叫sigmoid函数)，根据sigmoid函数值与阈值的关系，进行分类。也就是说logistic分类器是由一组权值系数组成，最关键的问题就是如何求得这组权值。

---

数据集加载

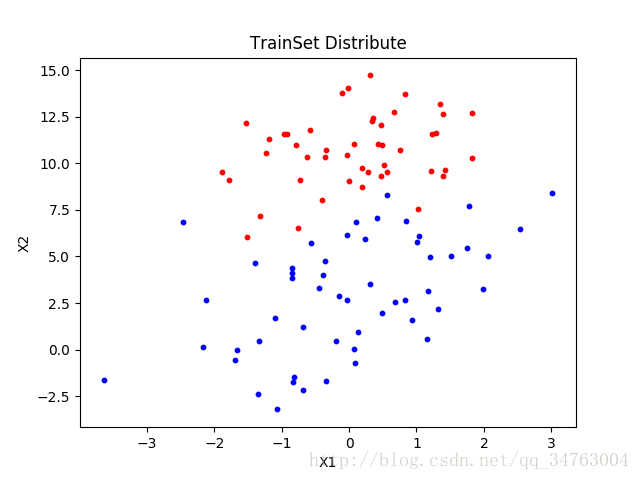
观察样本分布

#!/bin/usr/python
# -*- coding:utf-8 -*-
from numpy import *
from matplotlib import pyplot as plt

def loadDataSet(fileName):
    data = []
    dataSet = []
    dataMat = []
    labelMat = []
    fr = open(fileName)
    [data.append(line.strip('\r\n').split('\t')) for line in fr.readlines()]
    [dataSet.append([int(1),float(line[0]), float(line[1]),int(line[2])]) for line in data]
    for line in dataSet:
        dataMat.append(line[0:3])
        labelMat.append(line[-1])
    return dataSet,dataMat,labelMat  # return train set

def show(dataSet):
    data0 = []
    data1 = []
    [data0.append(line) for line in dataSet if line[3]==0]
    [data1.append(line) for line in dataSet if line[3]==1]
    for line in data0:
        plt.scatter(line[1:2], line[2:3], marker='o', color='r', label='Class 0', s=10) # label = 0
    for line in data1:
        plt.scatter(line[1:2], line[2:3], marker='o', color='b', label='Class 1', s=10) # label = 1
    plt.xlabel("X1")
    plt.ylabel("X2")
    plt.title('TrainSet Distribute')
    plt.show()

可以看出，存在‘某’条最佳拟合直线，将数据集分为两类

训练集和测试集选择

提供100个样本，随机选择其中54个作为训练集，另外46个作为测试集

---

Sigmoid函数权值计算

σ（z）=1(1+e−z)

z=ω0x0+ω1x1+...+ωnxn

或

z=ωTx

该函数被称为Sigmoid函数，当x=0时，Sigmoid的函数值为0.5,随着x的减小，函数值趋近与0;随着x的增大，函数值趋近于1;满足在跳跃点上从0到1的瞬间跳跃。其中，向量x是输入数据，向量w是最佳权值系数。

---

最佳回归系数的确定–梯度上升

主要思想

要找某个函数的最大值，最优方法是沿着该函数的梯度方向寻找。

梯度计算

函数f(x,y)的梯度可以如下表示，前提是函数f(x,y)必须在待计算的点上有定义并且可微。

在梯度上升法中，待计算点沿梯度方向每移动一步，都是朝着函数值增长最快的方向。 迭代停止条件为：迭代次数达到某个指定的值或者算法达到某个可以允许的误差范围。若移动的步长记作a，则梯度算法的迭代公式如下：

伪码描述

每个回归系数初始化为1
循环i次：
    计算整个数据集的梯度
    使用a * giradient更新回归系数向量
    返回回归系数向量

梯度上升实现

def sigmoid(z):
    return 1.0 / (1 + exp(-z))

def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)             
    labelMat = mat(classLabels).transpose() 
    m,n = shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = ones((n,1))
    for k in range(maxCycles):             
        h = sigmoid(dataMatrix*weights)     
        error = (labelMat - h)             
        weights = weights + alpha * dataMatrix.transpose()* error 
    return weights

得到最佳回归系数：

---

测试算法

def performanceTest(testMat, testLabelMat,weight):
    preSet = []
    count = 0
    numEntries = shape(testLabelMat)[0]
    testMat = mat(testMat)
    for i in xrange(numEntries):
        z = testMat[i] * weight
        res = sigmoid(z)
        if res < 0.5:
            preSet.append(0)
        else:
            preSet.append(1)
    for i in xrange(numEntries):
        if preSet[i]== testLabelMat[i]:
            count += 1;
    print '测试样本总数：{}'.format(numEntries)
    print '分类正确总数：{}'.format(count)
    print '分类错误总数：{}'.format(numEntries-count)
    print '分类正确率：{}%'.format(int(100*(count*1.0/numEntries)))

main函数：

def main():
    trainSet, trainMat, trainLabelMat = loadDataSet('/home/hu/文档/ML/machinelearning/Ch05/test.txt')
    testSet, testMat, testLabelMat = loadDataSet('/home/hu/文档/ML/machinelearning/Ch05/train.txt')

    weight = gradAscent(trainMat,trainLabelMat)
    performanceTest(testMat, testLabelMat,weight)

    # show(trainSet)
    # show(testSet)

if __name__=='__main__':
  main()

训练集和测试集互换后：

小结

1. 最佳回归参数的值受到 步长alpha 和 maxCycles 的影响，尚未对二者的影响作改进;
2. 每次更新回归系数时需要遍历整个训练集，在训练集规模较小的情况下尚可采用此方法，当训练集规模较大时此方法需要改进。