使用TensorFlow训练MNIST数据集

这篇教程主要来源于这本书：《21个项目玩转深度学习 基于TensorFlow的实践详解》
在线阅读：http://yuedu.163.com/book_reader/acc0e605a6b948b9983afcf62e297fba_4

当我们学习编程语言时，第一课通常会学习一个简单的 “Hello World” 程序， 而 MNIST 手写字符识别可以算得上是机器学习界的 “Hello World” 。 MNIST是由 Yann LeCun 等人建立的一个手写字符数据集。它简单易用，是一个很好的入门范例。这篇教程会以 MNIST 数据库为例， 用 TensorFlow 读取数据集中的数据， 并建立一个简单的图像识别模型。

一、MNIST数据集

1、mnist数据集简介

MNIST 数据集主要由一些手写数字的图片和相应的标签组成， 图片一共有 10 类， 分别对应从 0-9, 共10个阿拉伯数字。

                 MNIST数据集图片示例

原始的 MNIST 数据库一共包含下面 4 个文件：

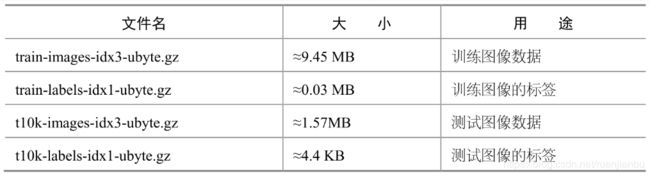
在MNIST数据集中有两类图像，一类是训练图像（对应文件train-images-idx3-ubyte.gz和train-labels-idx1-ubyte.gz），另一类是测试图像（对应文件 t10k-images-idx3-ubyte.gz 和 t10k-labels-idx1-ubyte.gz)。训练图像一共有60000张，供我们训练出合适的模型。测试图像一共有10000张，供我们测试训练的模型的性能。 在 TensorFlow 中，可以使用下面的 Python 代码下载 MNIST 数据。

代码中的print只是为了验证一下，下载部分其实只是前几行：

# coding:utf-8
# 从tensorflow.examples.tutorials.mnist引入模块。这是TensorFlow为了教学MNIST而提前编制的程序
from tensorflow.examples.tutorials.mnist import input_data
# 从MNIST_data/中读取MNIST数据。这条语句在数据不存在时，会自动执行下载
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

# 查看训练数据的大小
print(mnist.train.images.shape)  # (55000, 784)
print(mnist.train.labels.shape)  # (55000, 10)

# 查看验证数据的大小
print(mnist.validation.images.shape)  # (5000, 784)
print(mnist.validation.labels.shape)  # (5000, 10)

# 查看测试数据的大小
print(mnist.test.images.shape)  # (10000, 784)
print(mnist.test.labels.shape)  # (10000, 10)

# 打印出第0幅图片的向量表示
print(mnist.train.images[0, :])

# 打印出第0幅图片的标签
print(mnist.train.labels[0, :])

2.将MNIST数据集保存为图片

在原始的MNIST数据集中，每张图片都由一个28x28的矩阵表示。在TensorFlow中，变量mnist.train.images是训练样本，它的形状为（55000，784）。其中，5000是训练图像的个数，而784实际为单个样本的维数，即每张图片都由一个784维的向量表示（28x28=784）。可以使用下面的Python代码将 MNIST 数据集读取出来，并保存为图片文件。

代码中给出的是保存全部55000张图片，这需要一段时间，大家大可只保存几张，看看就好，在以后的训练中不会用到原图：

# coding: utf-8
from tensorflow.examples.tutorials.mnist import input_data
import scipy.misc
import os

# 读取MNIST数据集。如果不存在会事先下载。
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

# 我们把原始图片保存在MNIST_data/raw/文件夹下
# 如果没有这个文件夹会自动创建
save_dir = 'MNIST_data/raw/'
if os.path.exists(save_dir) is False:
    os.makedirs(save_dir)

# 保存train训练集全部55000张图片
for i in range(55000):
    # 请注意，mnist.train.images[i, :]就表示第i张图片（序号从0开始）
    image_array = mnist.train.images[i, :]
    # TensorFlow中的MNIST图片是一个784维的向量，我们重新把它还原为28x28维的图像。
    image_array = image_array.reshape(28, 28)
    # 保存文件的格式为 mnist_train_0.jpg, mnist_train_1.jpg, ... ,mnist_train_19.jpg
    filename = save_dir + 'mnist_train_%d.jpg' % i
    # 将image_array保存为图片
    # 先用scipy.misc.toimage转换为图像，再调用save直接保存。
    scipy.misc.toimage(image_array, cmin=0.0, cmax=1.0).save(filename)

print('Please check: %s ' % save_dir)

3、图像标签的独热表示

变量mnist.train.labels表示训练图像的标签，它的形状是（55000，10）。原始的图像标签是数字0-9，我们完全可以用一个数字来存储图像标签，但为什么这里每个训练标签是一个10维的向量呢？其实，这个10维的向量是原先类别号的独热（one-hot）表示。所谓独热表示，就是“一位有效编码”。我们用N维的向量来表示N个类别，每个类别占据独立的一位，任何时候独热表示中只有一位是“1”，其他都为“0”。我们可以从下面这个表格中理解独热表示：

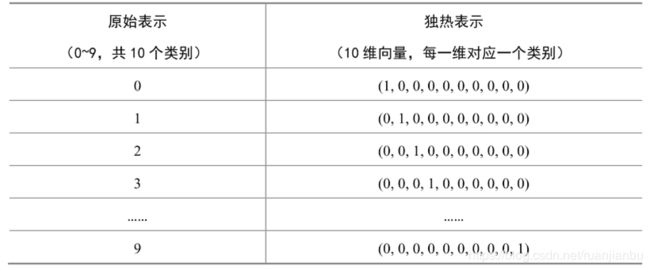
              类别的原始表示和独热表示

我们可以用下面的代码打印出前20张图片的标签，我们可以与刚才保存的图片对照，查看图像与图像的标签是否对应正确。

这次就更没有必要打印出所有的图片的标签了：

# coding: utf-8
from tensorflow.examples.tutorials.mnist import input_data
import numpy as np
# 读取mnist数据集。如果不存在会事先下载。
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

# 看前20张训练图片的label
for i in range(20):
    # 得到one-hot表示，形如(0, 1, 0, 0, 0, 0, 0, 0, 0, 0)
    one_hot_label = mnist.train.labels[i, :]
    # 通过np.argmax我们可以直接获得原始的label
    # 因为只有1位为1，其他都是0
    label = np.argmax(one_hot_label)
    print('mnist_train_%d.jpg label: %d' % (i, label))

至此，我们应当对变量mnist.train.images和mnist.train.labels很熟悉了。 剩下的mnist.validation.images、mnist.validation.labels、mnist.test.images、mnist. test. labels四个变量与它们非常类似，唯一的区别只是图像的个数不同，就不再做更详细的解释了。

二、利用TensorFlow识别MNIST

现在，我们将真正以TensorFlow为工具，使用Softmax回归写一个手写体数字识别程序。

1、Softmax回归在 TensorFlow 中的实现

我们先使用 TensorFlow定义了一个Softmax 模型，实现了 MNIST 数据集的分类。首先导入TensorFlow模块：

# 这句import tensorflow as tf是导入TensorFlow约定俗成的做法，请大家记住。
import tensorflow as tf

接下来，继续导入MNIST数据库：

# 导入MNIST教学的模块
from tensorflow.examples.tutorials.mnist import input_data
# 与之前一样，读入MNIST数据
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

下面的步骤是非常关键的几步，先来看代码：

# 创建x，x是一个占位符（placeholder），代表待识别的图片
x = tf.placeholder(tf.float32, [None, 784])

# W是Softmax模型的参数，将一个784维的输入转换为一个10维的输出
# 在TensorFlow中，变量的参数用tf.Variable表示
W = tf.Variable(tf.zeros([784, 10]))
# b是又一个Softmax模型的参数，我们一般叫做“偏置项”（bias）。
b = tf.Variable(tf.zeros([10]))

# y=softmax(Wx + b)，y表示模型的输出
y = tf.nn.softmax(tf.matmul(x, W) + b)

# y_是实际的图像标签，同样以占位符表示。
y_ = tf.placeholder(tf.float32, [None, 10])

这里定义了一些占位符（placeholder）和变量（Variable）。在TensorFlow中，无论是占位符还是变量，它们实际上都是"Tensor"。从TensorFlow的名字中，就可以看出Tensor在整个系统中处于核心地位。TensorFlow中的Tensor并不是具体的数值，它只是一些我们“希望”TensorFlow系统计算的“节点”。

这里的占位符和变量是不同类型的Tensor。占位符不依赖于其他的Tensor，它的值由用户自行传递给 TensorFlow，通常用来存储样本数据和标签。变量是指，在计算过程中可以改变的值，每次计算后，变量的值会被保存下来，通常用变量来存储模型的参数。

除了变量和占位符之外，还创建了一个 y = tf.nn.softmax(tf.matmul(x, W)+ b)。这个 y 就是一个依赖 x、W、b 的Tensor。如果要求TensorFlow计算 y 的值，那么系统首先会获取x、W、b 的值，再去计算 y 的值。

y 实际上定义了一个Softmax 回归模型。假设输入x的形状为(N，784)，其中 N 表示输入的训练图像的数目。W的形状为(784，10)，b 的形状为(10，_)。那么，Wx + b 的形状是(N，10)，即得到 y 的形状为(N，10)。也就是说，y 的每一行是一个10维的向量，表示模型预测的样本对应到各个类别的概率。

模型的输出是 y, 而实际的标签为 y_, 它们应当越相似越好。在 Softmax回归模型中，通常使用“交叉熵”损失来衡量这种相似性（这里的“熵”和在大学物理中给大家留下惨痛印象的“熵”不是一个东西哦！）。损失越小，模型的输出就和实际标签越接近，模型的预测也就越准确。

在TensorFlow中，这样定义交叉熵损失：

至此，我们得到了两个重要的Tensor：y和y_。
y是模型的输出，y_是实际的图像标签，不要忘了y_是独热表示的
下面我们就会根据y和y_构造损失
根据y, y_构造交叉熵损失
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y)))

构造完损失之后，下面一步是如何优化损失，让损失减小。这里使用梯度下降法优化损失，定义为：

有了损失，我们就可以用随机梯度下降针对模型的参数（W和b）进行优化
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)

TensorFlow默认会对所有变量计算梯度。在这里只定义了两个变量W和b ，因此程序将使用梯度下降法对W 、b 计算梯度并更新它们的值。tf.train.GradientDescentOptimizer (0.01) 中的 0.01 是梯度下降优化器使用的学习率（ Learning Rate ）。

在优化前，必须要创建一个会话（ Session ），并在会话中对变量进行初始化操作：

# 创建一个Session。只有在Session中才能运行优化步骤train_step。
sess = tf.InteractiveSession()
# 运行之前必须要初始化所有变量，分配内存。
tf.global_variables_initializer().run()
print('start training...')

会话是Tensor Flow 的又一个核心概念。前面提到Tensor 是“希望”TensorFlow 进行计算的结点。而会话就可以看成对这些结点进行计算的上下文。之前还提到过，变量是在计算过程中可以改变值的Tensor ，同时变量的值会被保存下来。事实上，变量的值就是被保存在会话中的。在对变量进行操作前必须对变量进行初始化，实际上是在会话中保存变量的初始值。初始化所有变量的语句是tf.g lobal_variables_initializer( ).run( ) 。

有了会话，就可以对变量W 、b 进行优化了，优化的程序如下：

# 进行1000步梯度下降
for _ in range(1000):
    # 在mnist.train中取100个训练数据
    # batch_xs是形状为(100, 784)的图像数据，batch_ys是形如(100, 10)的实际标签
    # batch_xs, batch_ys对应着两个占位符x和y_
    batch_xs, batch_ys = mnist.train.next_batch(100)
    # 在Session中运行train_step，运行时要传入占位符的值
    sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

在会话中，不需要系统计算占位符的值，而是直接把占位符的值传递给会话。与变量不同的是，占位符的值不会被保存，每次可以给占位符传递不同的值。

运行完梯度下降后，可以检测模型训练的结果，对应的代码如下：

# 正确的预测结果
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
# 计算预测准确率，它们都是Tensor
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# 在Session中运行Tensor可以得到Tensor的值
# 这里是获取最终模型的正确率
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))  # 0.9185

模型预测y的形状是（N, 10），而实际标签y_的形状是（N, 10），其中N 为输入模型的样本个数。tf. argmax(y, 1）、tf. argmax(y_, 1）的功能是取出数组中最大值的下标，可以用来将独热表示以及模型输出转换为数字标签。假设传入四个样本，它们的独热表示y_为（需要通过sess . run(y＿） 才能获取此 Tensor的值）。

得到了预测的标签和实际标签，接下来通过tf.equal 函数来比较它们是否相等，并将结果保存到correct_prediction 中。

最后，用tf.reduce_mean 可以计算数组中的所有元素的平均值，相当于得到了模型的预测准确率。

2、两层卷积网络分类

这里定义了四个函数和两个卷积层：

def weight_variable(shape):
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)

def bias_variable(shape):
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)

def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
                          strides=[1, 2, 2, 1], padding='SAME')

# 第一层卷积层
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)

函数weight_variable 可以返回一个给定形状的变量并自动以截断正态分布初始化， bias_variabale 同样返回一个给定形状的变量，初始化时所有值是0.1，可分别用这两个函数创建卷积的核（kernel）与偏置(bias）。

h_conv1 = tf.nn.relu(conv2d(x_image, W _conv1) + b_conv1 ）是真正进行卷积计算，卷积计算后选用ReLU 作为激活函数。

h_pool1 =max_pool_2x2(h_conv1）是调用函数max_pool_2x2 进行一次池化操作。

卷积、激活函数、池化，可以说是一个卷积层的 “标配”，通常一个卷积层都会包含这三个步骤，有时也会去掉最后的池化操作。

对第一次卷积操作后产生的h_pool1再做一次卷积计算，使用的代码与上面类似。

# 第二层卷积层
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)

两层卷积层之后是全连接层：

# 全连接层，输出为1024维的向量
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
# 使用Dropout，keep_prob是一个占位符，训练时为0.5，测试时为1
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

最后，再加入一层全连接，把上一步得到h_fc1_drop转换为10个类别的打分。

# 把1024维的向量转换成10维，对应10个类别
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.matmul(h_fc1_drop, W_fc2) + b_fc2

三、总结

最后，我们将以上的部分合到一起，就组成了一个完整的tensorflow训练MNIST数据集的程序。

下面给出的代码中进行了20000步训练，可使准确率达到99%。为了节省时间，大家也可以减小训练的步数（就是for循环里的值），来体会整个训练过程。代码奉上：

# coding: utf-8
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data


def weight_variable(shape):
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)


def bias_variable(shape):
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)


def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')


def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
                          strides=[1, 2, 2, 1], padding='SAME')


if __name__ == '__main__':
    # 读入数据
    mnist = input_data.read_data_sets("MNIST_data/MNIST_data/", one_hot=True)
    # x为训练图像的占位符、y_为训练图像标签的占位符
    x = tf.placeholder(tf.float32, [None, 784])
    y_ = tf.placeholder(tf.float32, [None, 10])

    # 将单张图片从784维向量重新还原为28x28的矩阵图片
    x_image = tf.reshape(x, [-1, 28, 28, 1])

    # 第一层卷积层
    W_conv1 = weight_variable([5, 5, 1, 32])
    b_conv1 = bias_variable([32])
    h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
    h_pool1 = max_pool_2x2(h_conv1)

    # 第二层卷积层
    W_conv2 = weight_variable([5, 5, 32, 64])
    b_conv2 = bias_variable([64])
    h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
    h_pool2 = max_pool_2x2(h_conv2)

    # 全连接层，输出为1024维的向量
    W_fc1 = weight_variable([7 * 7 * 64, 1024])
    b_fc1 = bias_variable([1024])
    h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
    h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
    # 使用Dropout，keep_prob是一个占位符，训练时为0.5，测试时为1
    keep_prob = tf.placeholder(tf.float32)
    h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

    # 把1024维的向量转换成10维，对应10个类别
    W_fc2 = weight_variable([1024, 10])
    b_fc2 = bias_variable([10])
    y_conv = tf.matmul(h_fc1_drop, W_fc2) + b_fc2

    # 我们不采用先Softmax再计算交叉熵的方法，而是直接用tf.nn.softmax_cross_entropy_with_logits直接计算
    cross_entropy = tf.reduce_mean(
        tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y_conv))
    # 同样定义train_step
    train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

    # 定义测试的准确率
    correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

    # 定义saver
    saver = tf.train.Saver()

    # 创建Session和变量初始化
    sess = tf.InteractiveSession()
    sess.run(tf.global_variables_initializer())

    # 训练20000步
    for i in range(20000):
        batch = mnist.train.next_batch(50)
        # 每100步报告一次在验证集上的准确度
        if i % 100 == 0:
            train_accuracy = accuracy.eval(feed_dict={
                x: batch[0], y_: batch[1], keep_prob: 1.0})
            print("step %d, training accuracy %g" % (i, train_accuracy))
        train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})

    # 模型储存位置
    saver.save(sess, 'D:/Reborn/正式入队/SAVE/model.ckpt')

    # 训练结束后报告在测试集上的准确度
    print("test accuracy %g" % accuracy.eval(feed_dict={
        x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))

以上这些就是tensorflow训练MNIST数据集的全部教程啦！感谢大家的支持！