已知两点经纬度,求一点相对于另一点方位角和两点间的距离
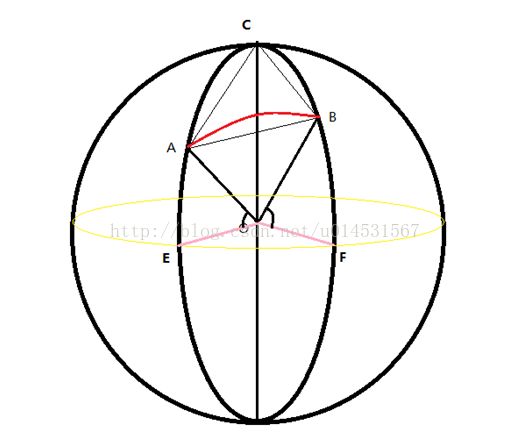
如上图所示,我们已经知道点A(Lng1,Lat1)和点B(Lng2,Lat2)的经纬度,所以有 ∠AOE =Lat1, ∠BOF=Lat2, ∠EOF=Lng2-Lng1.现在我们要求B点相对于A点方位角,等价于求二面角C-OA-B.
首先我们先求∠AOB.由三面角余弦定理可得 cos(∠AOB) = cos(∠AOC)cos(∠BOC) +sin(∠AOC) sin(∠BOC) cos(lng2-lng1)
= sin(Lat1)sin(Lat2)+ cos(Lat1) cos(Lat2) cos(lng2-lng1)
由半倍角 sin2(∠AOB/2) = (1– cos(∠AOB)) /2 有
sin2(∠AOB/2)= sin2((Lat1- Lat2)/2) + cos(Lat1)cos(Lat2)sin2((lng2- lng1)/2) 此公式是谷歌地图用来计算距离的公式.
第二步: sin(∠AOB) =sqrt( 1 – cos2(∠AOB) )
由球面正弦公式可得 sin(∠C-OA-B) =sin(∠BOC) sin(A-OC-B) / sin(∠AOB)
由此可得∠C-OA-B =arcsin(sin(∠BOC) sin(A-OC-B) / sin(∠AOB) )
如果要求球面AB 的距离 AB = R * rad(∠AOB)
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------球面正弦公式 -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
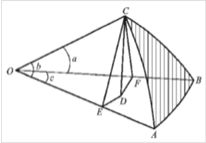
取球面三角形ABC,做球心三面角O-ABC。过C点做OAB平面的垂线交此平面于D,再从D向OA、OB引垂线DE,DF。连接CE和CF;由此得四个平面三角形OEC、OFC、CDE、CDF。因CD垂直于平面OAB,DE⊥OA,所以OA⊥CE;同理OB⊥CF,因此,四个平面三角形OEC、OFC、CDE、CDF都是直角三角形,并且有∠CED=A,∠CFD=B。从图中可得 sina/sinA =(CF/OC)/(CD/CE)=(CF·CE)/(OC·CD) 和 sinb/sinB =(CE/OC)/(CD/CF)=(CF·CE)/(OC·CD)
因得 sina/sinA= sinb/sinB. 利用轮换变更字母法,可以得出其它两个类似的式子,最后得 sina/sinA= sinb/sinB= sinc/sinC
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------三面角余弦理------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
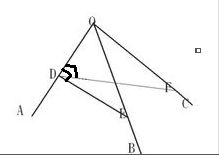
首先我们要求出∠AOB.先介绍下三面角余弦理.如图三面体OAB,OBC, OAC.取OA上一点D作线段DE和DF分别垂直于OA并交OB,OC于E,F.
假设我们已知∠AOB, ∠AOC和二面角B-OA-C亦即∠EDF.现求∠BOC.由余弦定理有
cos∠BOC = (OE2 +OF2 –EF2)/2OE*OF
OE = OD/cos(∠AOB), OF=OD/cos(∠AOC)
在三角形DEF中,由余弦定理有
EF2 = DE2+DF2-2DE*DF cos∠EDF
DE=OD tan∠AOB , DF = OD tan ∠AOC
联立以上各式并消去OD可得
cos∠BOC=cos∠AOB cos∠AOC + sin∠AOB sin∠AOC cos∠EDF
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------