2019 杭电多校训练赛 1011 Keen On Everything But Triangle（主席树模版，教学视频）

2019 杭电多校训练赛 1011 Keen On Everything But Triangle（主席树模版）

题目：

http://acm.hdu.edu.cn/showproblem.php?pid=6601

题意：

给你n组数据，m次查询。问区间[l,r]能组成的最大的三角形周长为多少，不能构成三角形则输出-1

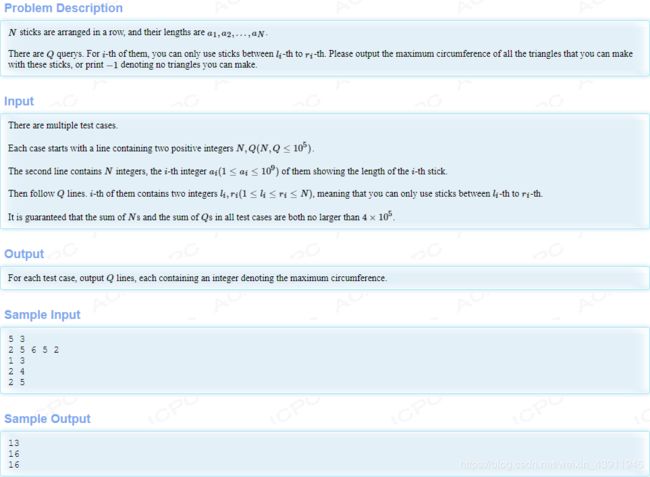
给个截屏可以看下数据范围

题解

多的都不说了，大比赛的时候给这道题摁在地上摩擦，一直想用莫队算法，结果都是TLE。可惜了没学过主席树呀！
这道题就是一道主席树的模版题，主席树可以在线询问区间【l,r】的第k小值。
小编这里就不讲主席树是怎么写的了（偷偷告诉你们我是在b站学的~）
主席树学习视频：https://www.bilibili.com/video/av56485341/

注意：

1. 数据是1e9，我们要把模版改一改，改成long long（这里wa过1发）
2. 区间【l，r】范围小于三的时候直接输出-1！（我在这个点wa了3发）
3. 主席树求的是第k小，所以我们k要从l-r+1递减。能构成三角形就退出循环，不能构成三角形就查找下一个最大值，这里我们用max1,max2,max3(max1>max2>max3)去维护最大的三个值
4. 如果前49个数都不能构成三角形，那么这个区间一定不能构成三角形了，因为我们可以通过斐波那契数列【1，1，2，3，5，8，13，21，34，55，89……】知道第49位就爆long long了，所以这里的找第k大值的时间复杂度可以忽略不计哦~

最后附上AC代码

#include<stdio.h>
#include<vector>
#include<algorithm>
#define ll long long
using namespace std;
vector<ll> v;
const int maxn = 2e5+5;
struct node{
	int l,r,sum;
}hjt[maxn*40];
int cnt,root[maxn]; 
ll a[maxn];
void init()
{
	cnt = 0;
	hjt[cnt].l = 0;
	hjt[cnt].r = 0;
	hjt[cnt].sum = 0;
	root[cnt] = 0;
	v.clear();
}
void insert(int l,int r,int pre,int &now,int p)
{
	hjt[++cnt] = hjt[pre];
	now = cnt;
	hjt[now].sum++;
	if(l==r) return;
	int mid = (l+r)>>1;
	if(p<=mid) insert(l,mid,hjt[pre].l,hjt[now].l,p);
	else insert(mid+1,r,hjt[pre].r,hjt[now].r,p);
}
int query(int l,int r,int L,int R,int k)
{
	if(l==r) return l;
	int mid = (l+r)>>1;
	int temp = hjt[hjt[R].l].sum - hjt[hjt[L].l].sum;//左子树数值只差
	if(k<=temp) return query(l,mid,hjt[L].l,hjt[R].l,k);
	else return  query(mid+1,r,hjt[L].r,hjt[R].r,k-temp);
}
int getid(ll x)
{
	return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
int main()
{
	int n,m;
	while(~scanf("%d %d",&n,&m))
	{
		init();
		for(int i=1;i<=n;i++)
		{
			scanf("%lld",&a[i]);
			v.push_back(a[i]);
		}
		sort(v.begin(),v.end());
		v.erase(unique(v.begin(),v.end()),v.end());//去重
		for(int i=1;i<=n;i++)
			insert(1,n,root[i-1],root[i],getid(a[i]));
		while(m--)
		{
			int l,r,k;
			scanf("%d %d",&l,&r);
			k = r-l+1;
			ll max1,max2,max3;
			ll ans = -1;
			if(k >= 3)
			{
				max1 = v[query(1,n,root[l-1],root[r],k)-1],k--;
				max2 = v[query(1,n,root[l-1],root[r],k)-1],k--;
				max3 = v[query(1,n,root[l-1],root[r],k)-1],k--;
				if(max3+max2 > max1)
					ans = max1+max2+max3;
				int cas = 3; 
				while(ans == -1 && k > 0 && cas <=50)
				{
					max1 = max2;
					max2 = max3;
					max3 = v[query(1,n,root[l-1],root[r],k)-1],k--;
					if(max3+max2 > max1)
						ans = max1+max2+max3;
					cas++;
				}
			}
			printf("%lld\n",ans);
		}
	}
	return 0;
 }