pytorch学习笔记（7）：RNN和LSTM实现分类和回归

参考文档：https://mp.weixin.qq.com/s/0DArJ4L9jXTQr0dWT-350Q

在第三篇文章中，我们介绍了 pytorch 中的一些常见网络层。但是这些网络层都是在 CNN 中比较常见的一些层，关于深度学习，我们肯定最了解的两个知识点就是 CNN 和 RNN。那么如何实现一个 RNN 呢？这篇文章我们用 RNN 实现一个分类器和一个回归器。

本文需要你最好对 RNN 相关的知识有一个初步的认识，然后我会尽可能的让你明白在 pytorch 中是如何去实现这一点的。

1、pytorch提供了哪些RNN？

如果我们对 RNN 有所了解，就会知道 RNN 有很多变种，就像 CNN 也有很多变种一样。只要带了 recurrent 的功能，就都属于 RNN 的范畴。那么在 pytorch 中提供了哪些 RNN 呢？

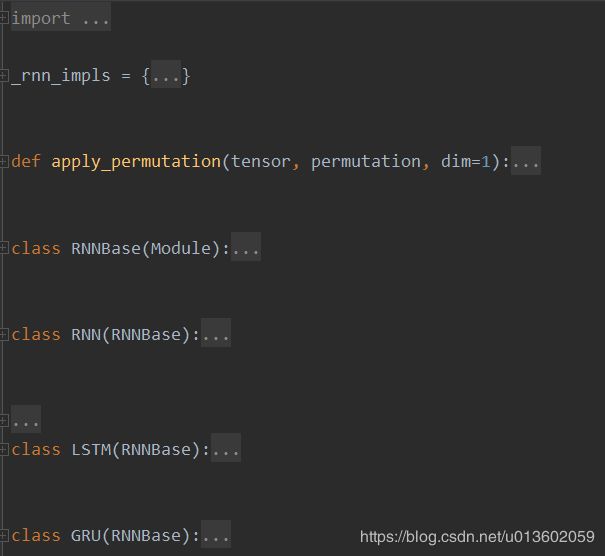
上面这幅图是 pytorch 源码中的结构，可以看到除了一个 RNNBase() 类，下面还有 RNN，LSTM，GRU 分别继承了 RNNBase() 类，实现了三个 RNN 子类。这三个也就是 pytorch 提供的 RNN 类型。

今天的文章，我们分别通过源码中的 doc 和一些介绍来了解 RNN 和 LSTM，然后分别用它们实现一个回归器和一个分类。关于 GRU 的部分，就留给大家自己去展开啦。

2、RNN，以及实现一个回归器

这一部分，我们先从 RNN 开始进行介绍，分别简单介绍一下 RNN 的原理，在 pytorch 中使用它的一些参数要求，最后是一个回归器，用 sin 曲线作为输入，cos 曲线作为 label，判断函数的拟合能力。

2.1、简单介绍RNN

首先看一下 RNN 的内容，常见的介绍 RNN 的文章中都会有这样一幅图：

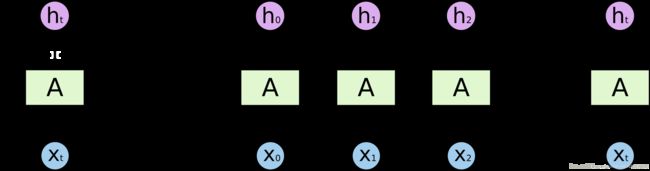
$X_0，X_1$ 等等分别是输入序列的一个维度上的数据，$X_0$ 首先传进去，生成 $h_0$ 作为第一个隐状态。然后 $h_0$ 和 $X_1$ 一起作为下一个时间序列上的输入，它们的输出再和 $X_2$ 作为下下个时间序列的输入，以此类推。

具体的细节我们就不展开讲了，默认大家对理论层面已经有了了解。在 pytorch 的源码 doc 中也给出了，对下面的公式进行计算：$$h_t=tanh(W_{ih}{x}_t+b_{ih}+W_{hh}{h}_{(t-1)}+b_{hh})$$这个式子也是对于 RNN 的常见描述。$W_{ih}$ 表示对输入数据进行处理的权重，而 $W_{hh}$ 则表示对上一个时间序列的隐状态进行处理的权重。$b_{ih}$ 和 $b_{hh}$ 则分别是两个偏置项，有的公式里面不会给出这两项，也就是默认偏置为 0。

2.2、RNN类实现的参数要求

接下来我们看一下 pytorch 中的 RNN 类有什么参数吧。我们主要是对这几个参数进行介绍：

• input_size：这个参数表示的输入数据的维度。比如输入一个句子，这里表示的就是每个单词的词向量的维度。

• hidden_size ：可以理解为在 CNN 中，一个卷积层的输出维度一样。这里表示将前面的 input_size 映射到一个什么维度上。

• num_layers：表示循环的层数。举个栗子，将 num_layers 设置为 2，也就是将如前面图所示的两个 RNN 堆叠在一起，第一层的输出作为第二层的输入。默认为 1。

• nonlinearity：这个参数对激活函数进行选择，目前 pytorch 支持 tanh 和 relu，默认的激活函数是 tanh。

• bias：这个参数就是对前面公式中的 $b_{ih}$ 和 $b_{hh}$。来选择是否需要偏置项，默认为 True。

• batch_first：这个是我们数据的格式描述，在 pytorch 中我们经常以 batch 分组来训练数据。这里的 batch_size 表示 batch 是否在输入数据的第一个维度，如果在第一个维度则为 True，默认为 False，也就是第二个维度。

• dropout：这里就是对每一层的输出是否加一个 dropout 层，如果参数非 0，那么就会加上这个 dropout 层。值得注意的是，对最后的输出层并不会加，也就是这个参数只有在 num_layers 参数大于 1 的时候才有意义。默认为 0。

• bidirectional：如果为 True，则表示 RNN 网络为双向结构，默认为 False。

介绍完具体的参数，我们就可以很简单的直接构建一个 RNN 的网络了，这里必须的两个参数是 input_size，hidden_size，其余的参数都有默认值，而且也符合一般常见的需要。

2.3、用sin曲线来预测cos曲线

接下来我们利用上面的知识来实现一个例子，对应的输入是如图的 sin 函数，label 则是 cos 函数。我们用输入来拟合这个输出。

我们先看一下这个数据应该如何展示：

steps=np.linspace(0,np.pi*4,100,dtype=np.float32)
x_np=np.sin(steps)
y_np=np.cos(steps)

通过 numpy 我们可以构建出来想要的 sin 和 cos 曲线，这里的 x_np 作为数据，y_np 作为 label。就可以进行我们的网络构建了。

根据前面学习的各个参数的作用，我们就可以构建如下的网络结构：

class RNN(nn.Module):
    def __init__(self):
        super(RNN, self).__init__()

        self.rnn=nn.RNN(
            input_size=1,
            hidden_size=32,
            batch_first=True,
            num_layers=1,
        )

        self.out=nn.Linear(32,1)

    def forward(self,x,h_state):
        r_out,h_state=self.rnn(x,h_state)
        outs=[]
        for time_step in range(r_out.size(1)):
            outs.append(self.out(r_out[:,time_step,:]))

        return torch.stack(outs,dim=1),h_state

我们介绍一下这里的几个关键点，首先参数上比较简单，输入就是一个横坐标，所以 input_size 是 1；将其 embedding 到一个 32 维的空间上，所以 hidden_size 选择了 32，这个值当然可以选择其它的；一层的网络，所以 num_layers 设置为 1，其实默认值也是 1，这一步可以省略；最后关注一下 batch_first 为 True，是因为我们选择将输入的维度设置为（batch，time_step，input_size）。

值得注意的是 forward 函数中，我们构建了一个 outs，然后一直往进 append 数据，具体的原因是什么呢？

当 RNN 在处理数据的时候，每次的输入需要传进去一个 sequence，其中每个 entry 可以看做一个词，如前面理论部分的介绍，每个词向量的长度就是 input_size。但是每个 sequence 的长度呢？其实对应了 time_step，也就是每次输入多少个“词向量”。

所以在 forward 的函数中，第二个维度 time_step 就是序列的长度，在这个例子中就是每次给网络给多少个点的数据。这个 for 循环就是从 r_out 的第二个维度中选择，将每个 time_step 上的数据的映射结果拿出来，然后通过 out() 函数，也就是 full connected layer 进行处理。最后 append 的就是这个处理结果。

最后我们把训练过程展现出来看一看：

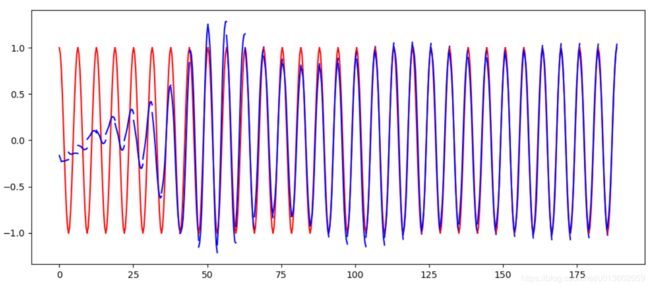
蓝色线条展示了模型的拟合过程，可以看到最终逐渐拟合到了目标的 cos 曲线上（红色线条）。

3、LSTM，以及实现一个分类器

前面我们介绍了原始的 RNN，众所周知的一些 RNN 的缺陷，我们就不赘述了（梯度爆炸，梯度消失等等）。那么 LSTM 成为了一个在序列化数据中非常受欢迎的选项。这一部分，我们先介绍一下简单的 LSTM 的理论基础，然后主要是 pytorch 中对于 LSTM 提供的接口，最后通过一个分类器的例子，来完成一个分类器。

3.1、简单介绍LSTM

和前面 RNN 一样，我们先甩出来一张大家肯定见过的图：

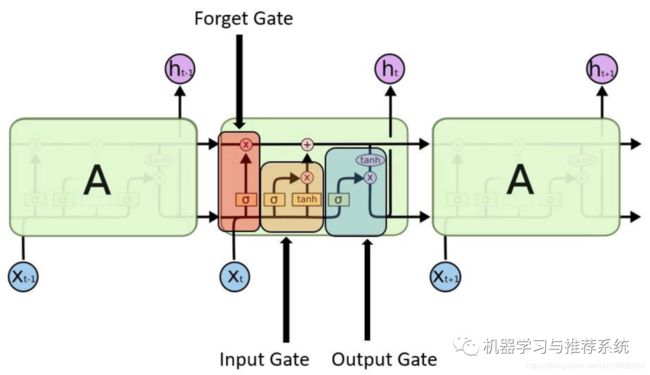
从图中可以看到，不同于 RNN，LSTM 提出了三个门（gate）的概念：input gate，forget gate，output gate。其实可以这样来理解，input gate 决定了对输入的数据做哪些处理，forget gate 决定了哪些知识被过滤掉，无需再继续传递，而 output gate 决定了哪些知识需要传递到下一个时间序列。

pytorch 中 LSTM 源码的 doc 中给出了以下公式：$$i_t=\sigma (W_{ii}{x}_t+b_{ii}+W_{hi}{h}_{(t-1)}+b_{hi})$$$$f_t=\sigma (W_{if}{x}_t+b_{if}+W_{hf}{h}_{(t-1)}+b_{hf})$$$$g_t=tanh(W_{ig}{x}_t+b_{ig}+W_{hg}{h}_{(t-1)}+b_{hg})$$$$o_t=\sigma (W_{io}{x}_t+b_{io}+W_{ho}{h}_{(t-1)}+b_{ho})$$$$c_t=f_t\ast c_{(t-1)}+i_t\ast g_t$$$$h_t=o_t\ast tanh(c_t)$$我们本篇文章不是专门介绍 LSTM 的文章，所以这里就不展开细讲。但是可以简略的帮大家回顾一下几个式子的整体流程。

• $i_t$是处理 input 的 input gate，外面一个 sigmoid 函数处理，其中的输入是当前输入 $x_t$ 和前一个时间状态的输出 $h_{(t-1)}$。所有的 $b$ 都是偏置项。

• $f_t$ 则是 forget gate 的操作，同样对当前输入 $x_t$ 和前一个状态的输出 $h_{(t-1)}$ 进行处理。

• $g_t$ 也是 input gate 中的操作，同样的输入，只是外面换成了 tanh 函数。

• $o_t$ 是前面图中 output gate 中左下角的操作，操作方式和前面 $i_t$，以及 $f_t$ 一样。

• $c_t$则是输出之一，对 forget gate 的输出，input gate 的输出进行相加，然后作为当前时间序列的一个隐状态向下传递。

• $h_t$ 同样是输出之一，对 前面的 $c_t$ 做一个 tanh 操作，然后和前面得到的 $o_t$ 进行相乘，$h_t$ 既向下一个状态传递，也作为当前状态的输出。

3.2、LSTM在pytorch中的参数要求

简单介绍完上面的数学内容，我们只需要知道 LSTM 内部进行了这些运算，具体的运算细节已经无需去自行设计，pytorch 已经给我们封装好了。

那么我们需要给它传入哪些输入，设置哪些参数呢？

class torch.nn.LSTM(*args, **kwargs)：
    input_size：x的特征维度
    hidden_size：隐藏层的特征维度
    num_layers：lstm隐层的层数，默认为1
    bias：默认为True
    batch_first：True则输入输出的数据格式为 (batch, seq, feature)
    dropout：除最后一层，每一层的输出都进行dropout，默认为: 0
    bidirectional：True则为双向lstm默认为False

看得出来，和前面的 RNN 参数非常相似，只少了一个 nonlinearty 参数。这是因为 LSTM 无需设置具体的非线性函数，从上面的公式中可以看到，具体每一步的操作，都已经有了清晰的定义。

所以这里的参数的意义就简略注释了，详细的意义和 RNN 一样。

3.3、在MNIST数据集上实现一个分类器

虽然说起 LSTM 大家肯定觉得是在 nlp 的数据集上比较常见，不过在图片分类中，它同样也可以使用。因为只是实现一个例子，所以我们就选择前面多次使用，比较熟悉的 mnist 进行验证吧。

我们知道 mnist 数据集是 28*28 的手写数字，而且因为是黑白照片，所以不像彩色图片一样是三通道，只有一个通道。

这里对于数据的理解，我们进行一下简单的介绍：对于每一张图片，我们看作一条数据，就像 nlp 中的一个句子一样。将照片的每一行看做一个向量，对应一个句子中的词向量，所以很显然，图片的行数就句子的长度。所以对这个 28*28 的照片，就是一个由 28 个向量组成的序列，且每个向量的长度都是 28。在 nlp 领域中，就是一个有 28 个单词的句子，且每个单词的词向量长度都为 28.

所以我们可以直接构建 LSTM 的网络结构如下：

class RNN(nn.Module):
    def __init__(self):
        super(RNN, self).__init__()

        self.rnn = nn.LSTM(
            input_size=28,
            hidden_size=64,
            num_layers=1,
            batch_first=True,
        )
        self.out = nn.Linear(64, 10)

    def forward(self, x):
        r_out, (h_n, h_c) = self.rnn(x, None)
        out = self.out(r_out[:, -1, :])
        return out

网络的结构方面需要介绍的不多，将一个 28 维的向量映射到 64 维的空间上，网络层数为 1，batch 在数据的第一个维度上。

对 forward 这里简单介绍一下，LSTM 的输出是由两部分组成，第一部分是 r_out，第二部分是 （h_n，h_c）。

对于 r_out 而言，就是最后一个状态的隐藏层的神经元的输出，换句话说，就是上面图片中各个 h_t 连起来的样子，如果是一个翻译的 LSTM，那就是翻译后的句子。

对于第二部分的两个参数而言，分别是最后一个状态的隐含层的隐状态，也就是上面图片中的两条向右一直传递的线，在最后一个状态的结果。

所以我们需要输出的是 out = r_out[:, -1, :]，如果不能理解是什么的话，我们先给出来 r_out 的 shape：（batch，seq_len，input_size）。现在是不是就明白了，这个 out 就是最后一个向量传进去 LSTM 后，得到的输出结果。也就是我们把图片的所有行都穿进去以后，LSTM 给出的分类结果。

接下来是对结果进行验证的部分，我们就不贴出来这部分代码了，意义不是很明显。

下面是我们对训练结果进行的测试，测试的效果自然不如 CNN 优秀，但是也到了 90% 左右了。

4、总结

今天的文章主要是介绍了 RNN 和 LSTM 在 pytorch 中的实现，前面也提到 pytorch 还提供了 GRU 的接口，感兴趣的朋友可以自行看看 doc，实现一个分类器或者回归器来进行接口验证。