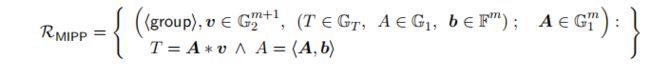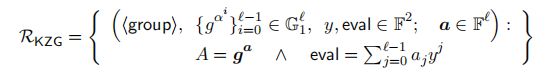双变量polynomial commitment
1. 引言
本博文主要研究的是 Benedikt Bünz 等人(standford,ethereum,berkeley) 2019年论文《Proofs for Inner Pairing Products and Applications》中的Pairing-based polynomial commitment schemes,其本质为 a generalization of two-tiered commitment scheme from Groth [Gro11] (Groth等人2011年论文Efficient Zero-Knowledge Arguments from Two-Tiered HomomorphicCommitments)。
前序博文为:Proofs for Inner Pairing Products and Applications 学习笔记
以下的“本文”是指:Benedikt Bünz 等人(standford,ethereum,berkeley) 2019年论文《Proofs for Inner Pairing Products and Applications》。
1.1 Polynomial commitment
Polynomial commitment由[KZG10] Kate等人 2010年论文《Constant-Size Commitments to Polynomials and Their Applications》 首次提出,具体是指:
- committer输出一个short commitment to polynomial;
- committer输出一个short proof (或者opening),用于证明the correctness of an evaluation of that committed polynomial at any point。
Polynomial commitment (PC) 在很多领域用于reduce communication and computation costs,如:
- proofs of storage and replication [XYZW16] [Fis18];
- anonymous credentials [CDHK15] [FHS19];
- verifiable secret sharing [KZG10] [BDK13];
- zero-knowledge arguments [WTSTW18] [MBKM19] [Gab19] [Set19] [GWC19] [XZZPS19] [CHMMVW20]。
本文将polynomial commitment与inner product argument结合,构建了a pairing based inner product argument,具有constant-sized commitments、logarithmic-sized openings 和 square root reference string。
本文采用了与[Gro11] 中类似的two-tiered homomorphic commitment,同时支持单变量和双变量多项式。本文提供了一种实例化方式,使得其同时具有public-coin setup, achieving square root verifier time以及upadatable SRS [GKMMM18],achieving log-time verification。
The transparent variant is secure in the plain model under the standard SXDH assumption,而本文的trusted setup scheme is secure in the algebraic group model (AGM) [FKL18]。本文的这种trusted setup scheme 具有的优势主要体现在produce opening proofs的时效上:
- 对于单变量多项式,opening cost为square root in the degree of the polynomial;
- 对于双变量多项式,opening cost为linear in the degree of one variable。
1.2 现有各种polynomial commitment对比
![]()
-
[KZG10] 的trusted setup scheme 支持constant proof size and verifier time (而本文的算法是logarithmic),但是本文的算法quadratically improve the opening efficiency,同时the maximum degree polynomial supported by a SRS of a given size。更小的SRS有助于节约storage,提升setup效率,而且还有助于security。
Gurk等人在论文[GGW18] 中指出,Cheon‘s attck on q-type assumption [Che10] can degrade the security of some SNARK schemes over BLS12-381 from the advertised 128 bits of security to 114 bits of security。
[KZG10] 论文中的scheme is secure under an updatable setup in the algebraic group model。 -
[Gro11] 论文中 designed a pairing based “batch product argument” secure under SXDH。该argument可看作是一种类型的polynomial commitment scheme。
-
[BG13] 论文中 Bayer和Groth designed a zero-knowledge proving system to show that a committed value is the correct evaluation of a known polynomial, under discrete-logarithm assumption。
-
[WTSTW18] 论文中 Wahby等人证明了可借用Bulletproofs中的inner product argument 来构建polynomial commitment scheme。
-
[BGH19] 论文中 Bowe等人证明了Bulletproofs的inner product argument 是可highly aggregatable to the point where aggregated proofs can be verified using a one off linear cost and an additional logarithmic factor per proof。
-
[ZXZS19] 论文中使用Reed-Solomon codes构建了polynomial commitment scheme。该论文中的commtiment使用了highly efficient symmetric key primitives,however the protocols that use them require soundness boosting techniques that result in large constant overheads。
-
[BFS19] 论文中 Bünz等人借助groups of unkown order such as RSA groups or class groups构建了polynomial commitment scheme,具有efficient verifier time and small proof size,但是需要super-linear commitment and prover time。
2. two-tiered homomorphic commitments
本文采用的是Groth [Gro11] (Groth等人2011年论文EfficientZero-KnowledgeArgumentsfromTwo-Tiered HomomorphicCommitments) 中的 two-tiered homomorphic commitments,即:commitments to commitments。
假设要commit to a polynomial:
f ( X , Y ) = f 0 ( Y ) + f 1 ( Y ) X + ⋯ + f m − 1 ( Y ) X m − 1 = ∑ i = 0 m − 1 f i ( Y ) X i f(X,Y)=f_0(Y)+f_1(Y)X+\cdots+f_{m-1}(Y)X^{m-1}=\sum_{i=0}^{m-1}f_i(Y)X^i f(X,Y)=f0(Y)+f1(Y)X+⋯+fm−1(Y)Xm−1=∑i=0m−1fi(Y)Xi
可将polynomial f ( X , Y ) f(X,Y) f(X,Y) 以矩阵形式表示为:【a polynomial of degree m − 1 m-1 m−1 in X X X and l − 1 l-1 l−1 in Y Y Y.】
f ( X , Y ) = ( 1 , X , X 2 , ⋯ , X m − 1 ) ( a 0 , 0 a 0 , 1 a 0 , 2 ⋯ a 0 , l − 1 a 1 , 0 a 1 , 1 a 1 , 2 ⋯ a 1 , l − 1 a 2 , 0 a 2 , 1 a 2 , 2 ⋯ a 2 , l − 1 ⋮ ⋱ ⋮ a m − 1 , 0 a m − 1 , 1 a m − 1 , 2 ⋯ a m − 1 , l − 1 ) ( 1 Y Y 2 ⋯ Y l − 1 ) = ( 1 , X , X 2 , ⋯ , X m − 1 ) A ( 1 Y Y 2 ⋯ Y l − 1 ) f(X,Y)=(1,X,X^2,\cdots,X^{m-1})\begin{pmatrix} a_{0,0} & a_{0,1} & a_{0,2} & \cdots & a_{0,l-1}\\ a_{1,0} & a_{1,1} & a_{1,2} & \cdots & a_{1,l-1}\\ a_{2,0} & a_{2,1} & a_{2,2} & \cdots & a_{2,l-1}\\ \vdots & & & \ddots & \vdots\\ a_{m-1,0} & a_{m-1,1} & a_{m-1,2} & \cdots & a_{m-1,l-1} \end{pmatrix} \begin{pmatrix} 1\\ Y\\ Y^2\\ \cdots \\ Y^{l-1} \end{pmatrix}=(1,X,X^2,\cdots,X^{m-1})\mathcal{A}\begin{pmatrix} 1\\ Y\\ Y^2\\ \cdots \\ Y^{l-1} \end{pmatrix} f(X,Y)=(1,X,X2,⋯,Xm−1)⎝⎜⎜⎜⎜⎜⎛a0,0a1,0a2,0⋮am−1,0a0,1a1,1a2,1am−1,1a0,2a1,2a2,2am−1,2⋯⋯⋯⋱⋯a0,l−1a1,l−1a2,l−1⋮am−1,l−1⎠⎟⎟⎟⎟⎟⎞⎝⎜⎜⎜⎜⎛1YY2⋯Yl−1⎠⎟⎟⎟⎟⎞=(1,X,X2,⋯,Xm−1)A⎝⎜⎜⎜⎜⎛1YY2⋯Yl−1⎠⎟⎟⎟⎟⎞
于是,polynomial f ( X , Y ) = ∑ i = 0 m − 1 f i ( Y ) X i f(X,Y)=\sum_{i=0}^{m-1}f_i(Y)X^i f(X,Y)=∑i=0m−1fi(Y)Xi,其中 f i ( Y ) = ∑ j = 0 l − 1 a i , j Y j f_i(Y)=\sum_{j=0}^{l-1}a_{i,j}Y^j fi(Y)=∑j=0l−1ai,jYj。
则commit to f ( X , Y ) f(X,Y) f(X,Y) 可表示为:
- 先对polynomials f 0 ( Y ) , ⋯ , f m − 1 ( Y ) f_0(Y),\cdots,f_{m-1}(Y) f0(Y),⋯,fm−1(Y)进行commit,相应的commitment值依次为 A 0 , ⋯ , A m − 1 A_0,\cdots,A_{m-1} A0,⋯,Am−1。
- 再对 A 0 , ⋯ , A m − 1 A_0,\cdots,A_{m-1} A0,⋯,Am−1进行commit,其commitment值为 T = C M ( A 0 , ⋯ , A m − 1 ) T=CM(A_0,\cdots,A_{m-1}) T=CM(A0,⋯,Am−1)。
![]()
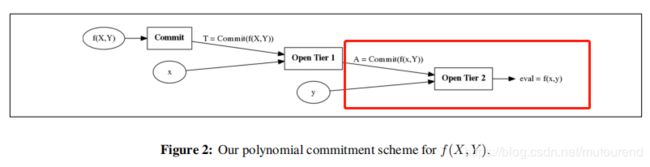
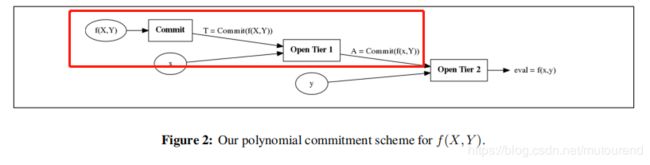
如上图所示,当收到challenge ( x , y ) (x,y) (x,y) 时,Prover:
- 先在第一层 evalute at x x x to obtain a commitment A A A to f ( x , Y ) f(x,Y) f(x,Y)。可通过multiexponentiation IPP argument (MIPP) 来实现。
- 然后在第二层 open commitment A A A at y y y 来获取 e v a l = f ( x , y ) eval=f(x,y) eval=f(x,y)。这可利用单变量polynomial commitment scheme来实现。
– 若在第二层采用Bulletproofs (Bünz等人2018年论文 [BBBPWM18] Bulletproofs: Short Proofs for Confidential Transactions and More)方式来实现,则对应的是transparent version。
– 若在第二层采用的是KZG方式,则对应的是structured setup version。
2.0 MIPP (multiexponentiation inner pairing product argument)
具体的信息为:
- public info: v ⃗ ∈ G 2 m , T ∈ G T , A ∈ G 1 , b ⃗ ∈ F m \vec{v}\in\mathbb{G}_2^m,T\in\mathbb{G}_T, A\in\mathbb{G}_1,\vec{b}\in\mathbb{F}^m v∈G2m,T∈GT,A∈G1,b∈Fm
- private info: A ⃗ ∈ G 1 m \vec{A}\in\mathbb{G}_1^m A∈G1m
- 待证明: T = A ⃗ ∗ v ⃗ = e ( A 0 , v 0 ) ⋯ e ( A m − 1 , v m − 1 ) ∧ A = < A ⃗ , b ⃗ > = A 0 b 0 ⋯ A m − 1 b m − 1 T=\vec{A}*\vec{v}=e(A_0,v_0)\cdots e(A_{m-1},v_{m-1})\wedge A=<\vec{A},\vec{b}>=A_0^{b_0}\cdots A_{m-1}^{b_{m-1}} T=A∗v=e(A0,v0)⋯e(Am−1,vm−1)∧A=<A,b>=A0b0⋯Am−1bm−1
1)为了使 A ⃗ ∈ G 1 m \vec{A}\in\mathbb{G}_1^m A∈G1m为private信息,需要基于 q q q-DBP assumption 或 q q q-ASDBP assumption来构建 T = A ⃗ ∗ v ⃗ = e ( A 0 , v 0 ) ⋯ e ( A m − 1 , v m − 1 ) T=\vec{A}*\vec{v}=e(A_0,v_0)\cdots e(A_{m-1},v_{m-1}) T=A∗v=e(A0,v0)⋯e(Am−1,vm−1),以此来证明Prover确实知道相应的 ( A 0 , ⋯ , A m − 1 ) (A_0,\cdots,A_{m-1}) (A0,⋯,Am−1)。
2)其实此时MIPP中的 b ⃗ = ( 1 , x , x 2 , ⋯ , x m − 1 ) \vec{b}=(1,x,x^2,\cdots,x^{m-1}) b=(1,x,x2,⋯,xm−1)。并注意此处的 x x x代表的是evaluate的 X X X值,与后面的challenge x x x的含义不同。
3)当采用structured版本时,由于 b ⃗ = ( 1 , x , x 2 , ⋯ , x m − 1 ) = ( 1 , b , b 2 , ⋯ , b m − 1 ) \vec{b}=(1,x,x^2,\cdots,x^{m-1})=(1,b,b^2,\cdots,b^{m-1}) b=(1,x,x2,⋯,xm−1)=(1,b,b2,⋯,bm−1),Verifier在做 b ⃗ ′ = x − 1 b ⃗ [ m ′ : ] + b ⃗ [ : m ′ ] \vec{b}'=x^{-1}\vec{b}_{[m':]}+\vec{b}_{[:m']} b′=x−1b[m′:]+b[:m′]的递归计算时,不需要在每个round都做计算,可采用delay computing的方式直接在最后一轮计算 b = ∏ j = 0 k ( x k − j − 1 + b 2 j ) b=\prod_{j=0}^{k}(x_{k-j}^{-1}+b^{2^j}) b=∏j=0k(xk−j−1+b2j),其中 k = log ( m ) k=\log(m) k=log(m)。在structured版本中,采用这种delaly computing,可节约verifier的时间 logarithmically。

2.1 transparent版本的双变量polynomial commitment【即无需trusted setup】
假设 f ( X , Y ) = ∑ i = 0 m − 1 f i ( Y ) X i , f i ( Y ) = ∑ j = 0 l − 1 a i , j Y j f(X,Y)=\sum_{i=0}^{m-1}f_i(Y)X^i,f_i(Y)=\sum_{j=0}^{l-1}a_{i,j}Y^j f(X,Y)=∑i=0m−1fi(Y)Xi,fi(Y)=∑j=0l−1ai,jYj为 a polynomial of degree m − 1 m-1 m−1 in X X X and l − 1 l-1 l−1 in Y Y Y。
则commitment key 应包含 l l l 个随机选择的generators in G 1 \mathbb{G}_1 G1 和 m m m 个随机选择的generators in G 2 \mathbb{G}_2 G2:
c k = ( g 0 , ⋯ , g l − 1 ) ∈ G 1 l , ( v 0 , ⋯ , v m − 1 ) ∈ G 2 m ck=(g_0,\cdots,g_{l-1})\in\mathbb{G}_1^l,(v_0,\cdots,v_{m-1})\in\mathbb{G}_2^m ck=(g0,⋯,gl−1)∈G1l,(v0,⋯,vm−1)∈G2m
2.1.1 Commit
进行commit,实际实现为:
-
首先,生成 m m m个generalized Pedersen commitments A 0 , ⋯ , A m − 1 A_0,\cdots,A_{m-1} A0,⋯,Am−1 to f 0 ( Y ) , ⋯ , f m − 1 ( Y ) f_0(Y),\cdots,f_{m-1}(Y) f0(Y),⋯,fm−1(Y):【即相当于对矩阵 A \mathcal{A} A逐行进行commit】
A i = P e d e r s e n C o m m i t ( a i , 0 , ⋯ , a i , l − 1 ) = g 0 a i , 0 ⋯ g l − 1 a i , l − 1 A_i=PedersenCommit(a_{i,0},\cdots,a_{i,l-1})=g_0^{a_{i,0}}\cdots g_{l-1}^{a_{i,l-1}} Ai=PedersenCommit(ai,0,⋯,ai,l−1)=g0ai,0⋯gl−1ai,l−1 -
然后,计算pairing commitment to the Pedersen commitments:
T = P a i r i n g C o m m i t ( A 0 , ⋯ , A m − 1 ) = ∏ i = 0 m − 1 e ( A i , v i ) T=PairingCommit(A_0,\cdots,A_{m-1})=\prod_{i=0}^{m-1}e(A_i,v_i) T=PairingCommit(A0,⋯,Am−1)=∏i=0m−1e(Ai,vi)
于是对双变量多项式的commitment为:
T = e ( g 0 a 0 , 0 ⋯ g l − 1 a 0 , l − 1 , v 0 ) ⋯ e ( g 0 a m − 1 , 0 ⋯ g l − 1 a m − 1 , l − 1 , v m − 1 ) T=e(g_0^{a_{0,0}}\cdots g_{l-1}^{a_{0,l-1}},v_0)\cdots e(g_0^{a_{m-1,0}}\cdots g_{l-1}^{a_{m-1,l-1}},v_{m-1}) T=e(g0a0,0⋯gl−1a0,l−1,v0)⋯e(g0am−1,0⋯gl−1am−1,l−1,vm−1)
该commitment 在 q q q-DBP assumption和 DL assumption 下具有binding属性。

2.1.2 对第一层进行evaluation
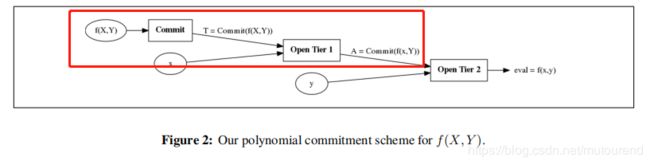
先在第一层 evalute at x x x to obtain a commitment A A A to f ( x , Y ) f(x,Y) f(x,Y)。可通过multiexponentiation IPP argument (MIPP) 来实现。
Transparent版本的MIPP算法为 M I P P t r a n s MIPP_{trans} MIPPtrans,其实现细节为:
- Setup:commitment key ( v 0 , ⋯ , v m − 1 ) ∈ G 2 m , h ^ ∈ G 2 (v_0,\cdots,v_{m-1})\in\mathbb{G}_2^m,\hat{h}\in\mathbb{G}_2 (v0,⋯,vm−1)∈G2m,h^∈G2,这些key之间为随机的,无明确关系。
- Initialize:Verifier发送a random challege c c c,Prover和Verifier均可计算 Z = T ⋅ e ( A , h ^ c ) Z=T\cdot e(A,\hat{h}^c) Z=T⋅e(A,h^c)。这样MIPP证明转换为证明Prover知道an opening A ⃗ ∣ ∣ A \vec{A}||A A∣∣A to Z Z Z under the commitment key v ⃗ ∣ ∣ h ^ c \vec{v}||\hat{h}^c v∣∣h^c,such that A = A ⃗ b ⃗ A=\vec{A}^{\vec{b}} A=Ab。
至此,具体信息调整为:【转换为博客 Proofs for Inner Pairing Products and Applications 学习笔记 4.4节中的GIPA证明 】
- public info: ( v ⃗ , h ^ c ) ∈ G 2 m + 1 , T ∈ G T , A ∈ G 1 , b ⃗ ∈ F m (\vec{v},\hat{h}^c)\in\mathbb{G}_2^{m+1}, T\in\mathbb{G}_T, A\in\mathbb{G}_1,\vec{b}\in\mathbb{F}^m (v,h^c)∈G2m+1,T∈GT,A∈G1,b∈Fm以及inner product commitment ( Z , b ⃗ ∈ F m ) (Z,\vec{b}\in\mathbb{F}^m) (Z,b∈Fm)
- private info: A ⃗ ∈ G 1 m \vec{A}\in\mathbb{G}_1^m A∈G1m
- 待证明: C M ( ( v ⃗ , 1 ⃗ , h ^ c ) , ( A ⃗ , b ⃗ , A ) ) = ( ( A ⃗ ∣ ∣ A ) ∗ ( v ⃗ ∣ ∣ h ^ c ) , b ⃗ ) = ( Z , b ⃗ ) CM((\vec{v},\vec{1},\hat{h}^c),(\vec{A},\vec{b},A))=((\vec{A}||A)*(\vec{v}||\hat{h}^c),\vec{b})=(Z,\vec{b}) CM((v,1,h^c),(A,b,A))=((A∣∣A)∗(v∣∣h^c),b)=(Z,b)【注意,其中 b ⃗ \vec{b} b为public info,故对应的commitment key选为 1 ⃗ \vec{1} 1。】
接下来为表述简洁,设置 h ^ = h ^ c \hat{h}=\hat{h}^c h^=h^c。
采用递归算法对以上 C M CM CM算法进行证明,在每一个round都对input vectors A ⃗ , b ⃗ \vec{A},\vec{b} A,b 和 commitment key v ⃗ \vec{v} v 进行二分fold为新的vectors A ⃗ ′ , b ⃗ ′ , v ⃗ ′ \vec{A}',\vec{b}',\vec{v}' A′,b′,v′ of length m ′ = m / 2 m'=m/2 m′=m/2,使得 Z ′ = ( A ⃗ ′ ∗ v ⃗ ′ ) ⋅ e ( A ′ , h ^ ) Z'=(\vec{A}'*\vec{v}')\cdot e(A',\hat{h}) Z′=(A′∗v′)⋅e(A′,h^) for A ′ = < A ⃗ ′ , b ⃗ ′ > A'=<\vec{A}',\vec{b}'> A′=<A′,b′>。
具体的实现为:
-
1)Prover的输入为 ( A ⃗ , b ⃗ , v ⃗ , Z , m ) (\vec{A},\vec{b},\vec{v},Z,m) (A,b,v,Z,m),设置 m ′ = m / 2 m'=m/2 m′=m/2,计算:
A ⃗ ′ = A ⃗ [ m ′ : ] x ∘ A ⃗ [ : m ′ ] \vec{A}'=\vec{A}_{[m':]}^x\circ\vec{A}_{[:m']} A′=A[m′:]x∘A[:m′]
b ⃗ ′ = x − 1 b ⃗ [ m ′ : ] + b ⃗ [ : m ′ ] \vec{b}'=x^{-1}\vec{b}_{[m':]}+\vec{b}_{[:m']} b′=x−1b[m′:]+b[:m′] 【Prover和Verifier均需计算】
v ⃗ ′ = v ⃗ [ m ′ : ] x − 1 ∘ v ⃗ [ : m ′ ] \vec{v}'=\vec{v}_{[m':]}^{x^{-1}}\circ\vec{v}_{[:m']} v′=v[m′:]x−1∘v[:m′]【Prover和Verifier均需计算】
有:
A ′ = < A ⃗ ′ , b ⃗ ′ > = ( < A ⃗ [ m ′ : ] , b ⃗ [ : m ′ ] > ) x ⋅ A ⋅ ( < A ⃗ [ : m ′ ] , b ⃗ [ m ′ : ] > ) x − 1 A'=<\vec{A}',\vec{b}'>=(<\vec{A}_{[m':]},\vec{b}_{[:m']}>)^x\cdot A\cdot (<\vec{A}_{[:m']},\vec{b}_{[m':]}>)^{x^{-1}} A′=<A′,b′>=(<A[m′:],b[:m′]>)x⋅A⋅(<A[:m′],b[m′:]>)x−1
A ⃗ ′ ∗ v ⃗ ′ = ( A ⃗ [ m ′ : ] ∗ v ⃗ [ : m ′ ] ) x ⋅ ( A ⃗ ∗ v ⃗ ) ⋅ ( A ⃗ [ : m ′ ] ∗ v ⃗ [ m ′ : ] ) x − 1 \vec{A}'*\vec{v}'=(\vec{A}_{[m':]}*\vec{v}_{[:m']})^x\cdot (\vec{A}*\vec{v})\cdot (\vec{A}_{[:m']}*\vec{v}_{[m':]})^{x^{-1}} A′∗v′=(A[m′:]∗v[:m′])x⋅(A∗v)⋅(A[:m′]∗v[m′:])x−1
为了使 Z ′ = ( A ⃗ ′ ∗ v ⃗ ′ ) ⋅ e ( A ′ , h ^ ) Z'=(\vec{A}'*\vec{v}')\cdot e(A',\hat{h}) Z′=(A′∗v′)⋅e(A′,h^) for A ′ = < A ⃗ ′ , b ⃗ ′ > A'=<\vec{A}',\vec{b}'> A′=<A′,b′>成立,于是有:
Z L = ( A ⃗ [ m ′ : ] ∗ v ⃗ [ : m ′ ] ) ⋅ e ( < A ⃗ [ m ′ : ] , b ⃗ [ : m ′ ] > , h ^ ) Z_L=(\vec{A}_{[m':]}*\vec{v}_{[:m']})\cdot e(<\vec{A}_{[m':]},\vec{b}_{[:m']}>,\hat{h}) ZL=(A[m′:]∗v[:m′])⋅e(<A[m′:],b[:m′]>,h^)
Z R = ( A ⃗ [ : m ′ ] ∗ v ⃗ [ m ′ : ] ) ⋅ e ( < A ⃗ [ : m ′ ] , b ⃗ [ m ′ : ] > , h ^ ) Z_R=(\vec{A}_{[:m']}*\vec{v}_{[m':]})\cdot e(<\vec{A}_{[:m']},\vec{b}_{[m':]}>,\hat{h}) ZR=(A[:m′]∗v[m′:])⋅e(<A[:m′],b[m′:]>,h^)
最终: Z ′ = Z L x ⋅ Z ⋅ Z R x − 1 Z'=Z_L^x\cdot Z\cdot Z_R^{x^{-1}} Z′=ZLx⋅Z⋅ZRx−1。 -
2)当 m ′ ≠ 1 m'\neq 1 m′=1时,设置 ( A ⃗ , b ⃗ , v ⃗ , Z , m ) = ( A ⃗ ′ , b ⃗ ′ , v ⃗ ′ , Z ′ , m ′ ) (\vec{A},\vec{b},\vec{v},Z,m)=(\vec{A}',\vec{b}',\vec{v}',Z',m') (A,b,v,Z,m)=(A′,b′,v′,Z′,m′),继续执行步骤1)。
-
3)当 m ′ = 1 m'=1 m′=1时,Prover发送 A = A ⃗ ′ ∈ G 1 , b = b ⃗ ′ , v = v ⃗ ′ , Z = Z ′ A=\vec{A}'\in\mathbb{G}_1,b=\vec{b}',v=\vec{v}',Z=Z' A=A′∈G1,b=b′,v=v′,Z=Z′,Verifier只需验证 Z = e ( A , v ) e ( A b , h ^ ) = e ( A , v h ^ b ) Z=e(A,v)e(A^b,\hat{h})=e(A,v\hat{h}^b) Z=e(A,v)e(Ab,h^)=e(A,vh^b)是否成立即可。
transparent 版本的MIPP实现 M I P P t r a n s MIPP_{trans} MIPPtrans的计算复杂度为:
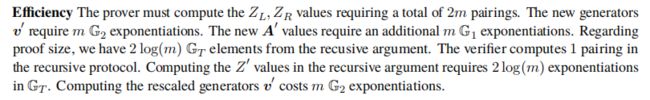
2.1.3 使用单变量polynomial commitment对第二层进行evaluation
- 在第一层用于evaluate T T T at x x x to a commitment A A A to f ( x , Y ) f(x,Y) f(x,Y);
- 在第二层用于evaluate the commitment A A A to f ( x , y ) f(x,y) f(x,y) at y y y。
第二层的polynomial可表示为 f ( x , Y ) = ∑ j = 0 l − 1 a j Y j f(x,Y)=\sum_{j=0}^{l-1}a_jY^j f(x,Y)=∑j=0l−1ajYj,对其的Pedersen commitment为:
A = g 0 a 0 ⋯ g l − 1 a l − 1 = g ⃗ a ⃗ A=g_0^{a_0}\cdots g_{l-1}^{a_{l-1}}=\vec{g}^{\vec{a}} A=g0a0⋯gl−1al−1=ga
假设 e v a l = f ( x , y ) eval=f(x,y) eval=f(x,y)。
基本信息为:
- public info:commitment key g ⃗ = ( g 0 , ⋯ , g l − 1 ) ∈ G 1 l \vec{g}=(g_0,\cdots,g_{l-1})\in\mathbb{G}_1^l g=(g0,⋯,gl−1)∈G1l, b ⃗ = ( 1 , y , ⋯ , y l − 1 ) ∈ F l , e v a l ∈ F , A ∈ G 1 \vec{b}=(1,y,\cdots,y^{l-1})\in\mathbb{F}^l,eval\in\mathbb{F},A\in\mathbb{G}_1 b=(1,y,⋯,yl−1)∈Fl,eval∈F,A∈G1
- private info: a ⃗ ∈ F l \vec{a}\in \mathbb{F}^l a∈Fl
- 待证明: A = g ⃗ a ⃗ ∧ e v a l = < a ⃗ , b ⃗ > A=\vec{g}^{\vec{a}}\wedge eval=<\vec{a},\vec{b}> A=ga∧eval=<a,b>
具体的实现为:
- Setup:commitment key g ⃗ = ( g 0 , ⋯ , g l − 1 ) ∈ G 1 l \vec{g}=(g_0,\cdots,g_{l-1})\in\mathbb{G}_1^l g=(g0,⋯,gl−1)∈G1l以及额外的random value u ∈ G 1 u\in\mathbb{G}_1 u∈G1。
- Initialize:Prover 发送 e v a l eval eval给Verifier;Verifier发送random challenge c c c。Prover和Verifier都计算 P = A ⋅ u c ⋅ e v a l P=A\cdot u^{c\cdot eval} P=A⋅uc⋅eval。接下来,Prover需要证明其知道 a vector a ⃗ \vec{a} a such that ( a ⃗ , e v a l ) (\vec{a},eval) (a,eval) is an evaluation to P P P under the commitment key ( g ⃗ , u c ) (\vec{g},u^c) (g,uc) such that e v a l = < a ⃗ , b ⃗ > eval=<\vec{a},\vec{b}> eval=<a,b>。
至此,具体信息调整为:【转换为博客 Proofs for Inner Pairing Products and Applications 学习笔记 4.4节中的GIPA证明 】
- public info: ( g ⃗ , u c ) ∈ G 1 l + 1 , e v a l ∈ F , A ∈ G 1 , b ⃗ ∈ F l (\vec{g},u^c)\in\mathbb{G}_1^{l+1}, eval\in\mathbb{F}, A\in\mathbb{G}_1,\vec{b}\in\mathbb{F}^l (g,uc)∈G1l+1,eval∈F,A∈G1,b∈Fl以及inner product commitment ( P ∈ G 1 , b ⃗ ∈ F l ) (P\in\mathbb{G}_1,\vec{b}\in\mathbb{F}^l) (P∈G1,b∈Fl)
- private info: a ⃗ ∈ F l \vec{a}\in\mathbb{F}^l a∈Fl
- 待证明: C M ( ( g ⃗ , 1 ⃗ , u c ) , ( a ⃗ , b ⃗ , e v a l ) ) = ( g ⃗ a ⃗ u c ⋅ e v a l , b ⃗ ) = ( P , b ⃗ ) CM((\vec{g},\vec{1},u^c),(\vec{a},\vec{b},eval))=(\vec{g}^{\vec{a}}u^{c\cdot eval},\vec{b})=(P,\vec{b}) CM((g,1,uc),(a,b,eval))=(gauc⋅eval,b)=(P,b)【注意,其中 b ⃗ \vec{b} b为public info,故对应的commitment key选为 1 ⃗ \vec{1} 1。】
接下来为表述简洁,设置 u = u c u=u^c u=uc。
采用递归算法对以上 C M CM CM算法进行证明,在每一个round都对input vectors a ⃗ , b ⃗ \vec{a},\vec{b} a,b 和 commitment key g ⃗ \vec{g} g 进行二分fold为新的vectors a ⃗ ′ , b ⃗ ′ , g ⃗ ′ \vec{a}',\vec{b}',\vec{g}' a′,b′,g′ of length m ′ = m / 2 m'=m/2 m′=m/2,使得 P ′ = g ⃗ ′ a ⃗ ′ u e v a l ′ P'=\vec{g}'^{\vec{a}'}u^{eval'} P′=g′a′ueval′ for e v a l ′ = < a ⃗ ′ , b ⃗ ′ > eval'=<\vec{a}',\vec{b}'> eval′=<a′,b′>。
具体的实现为:
-
1)Prover的输入为 ( a ⃗ , b ⃗ , g ⃗ , P , m ) (\vec{a},\vec{b},\vec{g},P,m) (a,b,g,P,m),设置 m ′ = m / 2 m'=m/2 m′=m/2,计算:
a ⃗ ′ = x a ⃗ [ m ′ : ] + a ⃗ [ : m ′ ] \vec{a}'=x\vec{a}_{[m':]}+\vec{a}_{[:m']} a′=xa[m′:]+a[:m′]
b ⃗ ′ = x − 1 b ⃗ [ m ′ : ] + b ⃗ [ : m ′ ] \vec{b}'=x^{-1}\vec{b}_{[m':]}+\vec{b}_{[:m']} b′=x−1b[m′:]+b[:m′] 【Prover和Verifier均需计算】
g ⃗ ′ = g ⃗ [ m ′ : ] x − 1 ∘ g ⃗ [ : m ′ ] \vec{g}'=\vec{g}_{[m':]}^{x^{-1}}\circ\vec{g}_{[:m']} g′=g[m′:]x−1∘g[:m′]【Prover和Verifier均需计算】
有:
e v a l ′ = < a ⃗ ′ , b ⃗ ′ > = x ( < a ⃗ [ : m ′ ] , b ⃗ [ m ′ : ] > ) ⋅ e v a l ⋅ x − 1 ( < a ⃗ [ m ′ : ] , b ⃗ [ : m ′ ] > ) eval'=<\vec{a}',\vec{b}'>=x(<\vec{a}_{[:m']},\vec{b}_{[m':]}>)\cdot eval \cdot {x^{-1}}(<\vec{a}_{[m':]},\vec{b}_{[:m']}>) eval′=<a′,b′>=x(<a[:m′],b[m′:]>)⋅eval⋅x−1(<a[m′:],b[:m′]>)
g ⃗ ′ a ⃗ ′ = ( g ⃗ [ : m ′ ] a ⃗ [ m ′ : ] ) x ⋅ g ⃗ a ⃗ ⋅ ( g ⃗ [ m ′ : ] a ⃗ [ : m ′ ] ) x − 1 \vec{g}'^{\vec{a}'}=(\vec{g}_{[:m']}^{\vec{a}_{[m':]}})^x\cdot \vec{g}^{\vec{a}}\cdot (\vec{g}_{[m':]}^{\vec{a}_{[:m']}})^{x^{-1}} g′a′=(g[:m′]a[m′:])x⋅ga⋅(g[m′:]a[:m′])x−1
为了使 P ′ = g ⃗ ′ a ⃗ ′ u e v a l ′ P'=\vec{g}'^{\vec{a}'}u^{eval'} P′=g′a′ueval′ for e v a l ′ = < a ⃗ ′ , b ⃗ ′ > eval'=<\vec{a}',\vec{b}'> eval′=<a′,b′>成立,于是有:
P L = g ⃗ [ m ′ : ] a ⃗ [ : m ′ ] ⋅ u < a ⃗ [ : m ′ ] , b ⃗ [ m ′ : ] > P_L=\vec{g}_{[m':]}^{\vec{a}_{[:m']}}\cdot u^{<\vec{a}_{[:m']},\vec{b}_{[m':]}>} PL=g[m′:]a[:m′]⋅u<a[:m′],b[m′:]>
P R = g ⃗ [ : m ′ ] v ⃗ [ m ′ : ] ⋅ u < a ⃗ [ m ′ : ] , b ⃗ [ : m ′ ] > P_R=\vec{g}_{[:m']}^{\vec{v}_{[m':]}}\cdot u^{<\vec{a}_{[m':]},\vec{b}_{[:m']}>} PR=g[:m′]v[m′:]⋅u<a[m′:],b[:m′]>
最终: P ′ = P L x ⋅ P ⋅ P R x − 1 P'=P_L^x\cdot P\cdot P_R^{x^{-1}} P′=PLx⋅P⋅PRx−1。 -
2)当 m ′ ≠ 1 m'\neq 1 m′=1时,设置 ( a ⃗ , b ⃗ , g ⃗ , P , m ) = ( a ⃗ ′ , b ⃗ ′ , g ⃗ ′ , P ′ , m ′ ) (\vec{a},\vec{b},\vec{g},P,m)=(\vec{a}',\vec{b}',\vec{g}',P',m') (a,b,g,P,m)=(a′,b′,g′,P′,m′),继续执行步骤1)。
-
3)当 m ′ = 1 m'=1 m′=1时,Prover发送 a = a ⃗ ′ ∈ F , b = b ⃗ ′ ∈ F , P = P ′ ∈ G 1 a=\vec{a}'\in\mathbb{F},b=\vec{b}'\in\mathbb{F},P=P'\in\mathbb{G}_1 a=a′∈F,b=b′∈F,P=P′∈G1,Verifier只需验证 P = g a u a ⋅ b P=g^au^{a\cdot b} P=gaua⋅b是否成立即可。
以上 R D L R_{DL} RDL关系的证明算法计算复杂度为:

2.2 structured setup版本的双变量polynomial commitment【即需要trusted setup】
假设 f ( X , Y ) = ∑ i = 0 m − 1 f i ( Y ) X i , f i ( Y ) = ∑ j = 0 l − 1 a i , j Y j f(X,Y)=\sum_{i=0}^{m-1}f_i(Y)X^i,f_i(Y)=\sum_{j=0}^{l-1}a_{i,j}Y^j f(X,Y)=∑i=0m−1fi(Y)Xi,fi(Y)=∑j=0l−1ai,jYj为 a polynomial of degree m − 1 m-1 m−1 in X X X and l − 1 l-1 l−1 in Y Y Y。
选择generator g ∈ G 1 , h ∈ G 2 g\in\mathbb{G}_1,h\in\mathbb{G}_2 g∈G1,h∈G2,则commitment key 应包含 l l l 个元素 in G 1 \mathbb{G}_1 G1 和 m m m 个 元素 in G 2 \mathbb{G}_2 G2:【trusted setup,需要选择随机数 α , β \alpha,\beta α,β】
c k = ( ( g 0 , ⋯ , g l − 1 ) = ( g , g α , ⋯ , g α l − 1 ) ∈ G 1 l , ( v 0 , ⋯ , v m − 1 ) = ( h , h β 2 , ⋯ , h β 2 m − 2 ) ∈ G 2 m ) ck=((g_0,\cdots,g_{l-1})=(g,g^{\alpha},\cdots,g^{\alpha^{l-1}})\in\mathbb{G}_1^l,(v_0,\cdots,v_{m-1})=(h,h^{\beta^2},\cdots,h^{\beta^{2m-2}})\in\mathbb{G}_2^m) ck=((g0,⋯,gl−1)=(g,gα,⋯,gαl−1)∈G1l,(v0,⋯,vm−1)=(h,hβ2,⋯,hβ2m−2)∈G2m)
2.2.1 commit
进行commit,实际实现为:
-
首先,生成 m m m个KZG polynomial commitments A 0 , ⋯ , A m − 1 A_0,\cdots,A_{m-1} A0,⋯,Am−1 to f 0 ( Y ) , ⋯ , f m − 1 ( Y ) f_0(Y),\cdots,f_{m-1}(Y) f0(Y),⋯,fm−1(Y):【即相当于对矩阵 A \mathcal{A} A逐行进行commit】
A i = K Z G C o m m i t ( a i , 0 , ⋯ , a i , l − 1 ) = g 0 a i , 0 ⋯ g l − 1 a i , l − 1 = g ∑ j = 0 l − 1 a i , j α j A_i=KZGCommit(a_{i,0},\cdots,a_{i,l-1})=g_0^{a_{i,0}}\cdots g_{l-1}^{a_{i,l-1}}=g^{\sum_{j=0}^{l-1}a_{i,j}\alpha^j} Ai=KZGCommit(ai,0,⋯,ai,l−1)=g0ai,0⋯gl−1ai,l−1=g∑j=0l−1ai,jαj -
然后,计算pairing commitment to the KZG commitments:
T = P a i r i n g C o m m i t ( A 0 , ⋯ , A m − 1 ) = ∏ i = 0 m − 1 e ( A i , v i ) = ∏ i = 0 m − 1 e ( A i , h β 2 i ) T=PairingCommit(A_0,\cdots,A_{m-1})=\prod_{i=0}^{m-1}e(A_i,v_i)=\prod_{i=0}^{m-1}e(A_i,h^{\beta^{2i}}) T=PairingCommit(A0,⋯,Am−1)=∏i=0m−1e(Ai,vi)=∏i=0m−1e(Ai,hβ2i)
于是对双变量多项式的commitment为:
T = e ( g , h ) ∑ i = 0 m − 1 ∑ j = 0 l − 1 a i , j α j β 2 i T=e(g,h)^{\sum_{i=0}^{m-1}\sum_{j=0}^{l-1}a_{i,j}\alpha^j\beta^{2i}} T=e(g,h)∑i=0m−1∑j=0l−1ai,jαjβ2i
该commitment 在 q q q-ASDBP assumption和 q q q-SDH assumption 下具有binding属性。
2.2.2 MIPP 对第一层进行evaluation
先在第一层 evalute at x x x to obtain a commitment A A A to f ( x , Y ) f(x,Y) f(x,Y)。可通过multiexponentiation IPP argument (MIPP) 来实现。
Structured版本的MIPP算法为 M I P P s r s MIPP_{srs} MIPPsrs,其实现细节为:
- Setup:commitment key ( g β ∈ G 2 , v ⃗ = { h β 2 i } i = 0 m − 1 ∈ G 2 m , h ^ ∈ G 2 ) (g^{\beta}\in\mathbb{G}_2,\vec{v}=\{h^{\beta^{2i}}\}_{i=0}^{m-1}\in\mathbb{G}_2^m,\hat{h}\in\mathbb{G}_2) (gβ∈G2,v={hβ2i}i=0m−1∈G2m,h^∈G2)。而对于Verifier,仅需要 g β ∈ G 2 , h ^ ∈ G 2 g^{\beta}\in\mathbb{G}_2,\hat{h}\in\mathbb{G}_2 gβ∈G2,h^∈G2。
- Initialize:Verifier发送a random challege c c c,Prover和Verifier均可计算 Z = T ⋅ e ( A , h ^ c ) Z=T\cdot e(A,\hat{h}^c) Z=T⋅e(A,h^c)。这样MIPP证明转换为证明Prover知道an opening A ⃗ ∣ ∣ A \vec{A}||A A∣∣A to Z Z Z under the commitment key v ⃗ ∣ ∣ h ^ c \vec{v}||\hat{h}^c v∣∣h^c,such that A = < A ⃗ , b ⃗ > = A ⃗ b ⃗ A=<\vec{A},\vec{b}>=\vec{A}^{\vec{b}} A=<A,b>=Ab。
与2.1.2类似,改为证明 C M ( ( v ⃗ , 1 ⃗ , h ^ c ) , ( A ⃗ , b ⃗ , A ) ) = ( ( A ⃗ ∣ ∣ A ) ∗ ( v ⃗ ∣ ∣ h ^ c ) , b ⃗ ) = ( Z , b ⃗ ) CM((\vec{v},\vec{1},\hat{h}^c),(\vec{A},\vec{b},A))=((\vec{A}||A)*(\vec{v}||\hat{h}^c),\vec{b})=(Z,\vec{b}) CM((v,1,h^c),(A,b,A))=((A∣∣A)∗(v∣∣h^c),b)=(Z,b)。
借助博客 Proofs for Inner Pairing Products and Applications 学习笔记 中5.2节的 R c k R_{ck} Rck 的polynomial commitment 来优化verifier计算recursive commitment key的算力。注意,此处只需关注 v ⃗ \vec{v} v即可。且此处不考虑aggregation,设置 r = 1 r=1 r=1,于是在最后一个round有:
v = h f v ( β ) v=h^{f_v(\beta)} v=hfv(β) for f v ( X ) = ∏ j = 0 l ( x l − j − 1 + X 2 j + 1 ) f_v(X)=\prod_{j=0}^{l}(x_{l-j}^{-1}+X^{2^{j+1}}) fv(X)=∏j=0l(xl−j−1+X2j+1)
最终Verifier仍然是验证 Z = e ( A , v ) e ( A b , h ^ ) = e ( A , v h ^ b ) Z=e(A,v)e(A^b,\hat{h})=e(A,v\hat{h}^b) Z=e(A,v)e(Ab,h^)=e(A,vh^b)是否成立以及对recursive commitment key v v v的相应的KZG proof是否成立。
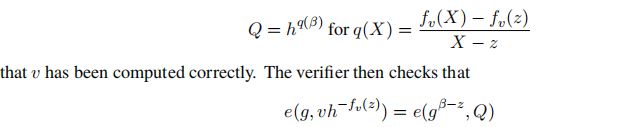
Structured 版本MIPP算法 M I P P s r s MIPP_{srs} MIPPsrs的计算复杂度为:

2.2.3 使用单变量polynomial commitment对第二层进行evaluation

Structured setup场景下,第二层的polynomial可表示为 f ( x , Y ) = ∑ j = 0 l − 1 a j Y j f(x,Y)=\sum_{j=0}^{l-1}a_jY^j f(x,Y)=∑j=0l−1ajYj,对其的KZG polynomial commitment为:
A = g 0 a 0 ⋯ g l − 1 a l − 1 = g ∑ j = 0 l − 1 a j α j A=g_0^{a_0}\cdots g_{l-1}^{a_{l-1}}=g^{\sum_{j=0}^{l-1}a_j\alpha^j} A=g0a0⋯gl−1al−1=g∑j=0l−1ajαj
假设 e v a l = f ( x , y ) eval=f(x,y) eval=f(x,y)。
基本信息为:
- public info:commitment key g ⃗ = { g α i } i = 0 l − 1 ∈ G 1 l \vec{g}=\{g^{\alpha^i}\}_{i=0}^{l-1}\in\mathbb{G}_1^l g={gαi}i=0l−1∈G1l, y ∈ F , e v a l ∈ F , A ∈ G 1 y\in\mathbb{F},eval\in\mathbb{F},A\in\mathbb{G}_1 y∈F,eval∈F,A∈G1
- private info: a ⃗ ∈ F l \vec{a}\in \mathbb{F}^l a∈Fl
- 待证明: A = g ⃗ a ⃗ ∧ e v a l = ∑ j = 0 l − 1 a j y j A=\vec{g}^{\vec{a}}\wedge eval=\sum_{j=0}^{l-1}a_jy^j A=ga∧eval=∑j=0l−1ajyj
3. 双变量polynomial commitment
将transparent 版本 2.1.2和2.1.3节(或 structured 版本 2.2.2和2.2.3节)的multiexponentiatiation argument 和 univariate polynomial commitment结合起来,就相当于是:
evaluate commitment T = ∏ i = 0 m − 1 e ( ∏ j = 0 l − 1 g j a i , j , v j ) T=\prod_{i=0}^{m-1}e(\prod_{j=0}^{l-1}g_j^{a_{i,j}},v_j) T=∏i=0m−1e(∏j=0l−1gjai,j,vj) to 双变量polynomials f ( X , Y ) = ∑ i , j = 0 m − 1 , l − 1 a i , j X i Y j = ∑ i = 0 m − 1 f i ( Y ) X i f(X,Y)=\sum_{i,j=0}^{m-1,l-1}a_{i,j}X^iY^j=\sum_{i=0}^{m-1}f_i(Y)X^i f(X,Y)=∑i,j=0m−1,l−1ai,jXiYj=∑i=0m−1fi(Y)Xi,其中 f i ( Y ) = ∑ j = 0 l − 1 a i , j Y j f_i(Y)=\sum_{j=0}^{l-1}a_{i,j}Y^j fi(Y)=∑j=0l−1ai,jYj。
接下来,需要分别说明无论是transparent 版本还是structured 版本双变量polynomial commitment 均为Extractable。

transparent 版本和 structured版本双变量polynomial commitment的性能对比为:

3.1 transparent版本的双变量polynomial commitment
为了evaluate a polynomial commitment T T T to e v a l = f ( x , y ) eval=f(x,y) eval=f(x,y):
- Prover首先计算 A = ∏ i = 0 m − 1 A i x i ∈ G 1 A=\prod_{i=0}^{m-1}A_i^{x^i}\in\mathbb{G}_1 A=∏i=0m−1Aixi∈G1,其中 A i = P e d e r s e n C o m m i t ( a i , 0 , ⋯ , a i , l − 1 ) = g 0 a i , 0 ⋯ g l − 1 a i , l − 1 A_i=PedersenCommit(a_{i,0},\cdots,a_{i,l-1})=g_0^{a_{i,0}}\cdots g_{l-1}^{a_{i,l-1}} Ai=PedersenCommit(ai,0,⋯,ai,l−1)=g0ai,0⋯gl−1ai,l−1。
- Prover需要证明 A A A的计算是正确的,可采用2.1.2节的MIPP argument来证明。
- 接下来Prover计算polynomial f ( x , Y ) = ∑ i = 0 m − 1 x i f i ( Y ) = ∑ j = 0 l − 1 a j Y j f(x,Y)=\sum_{i=0}^{m-1}x^if_i(Y)=\sum_{j=0}^{l-1}a_jY^j f(x,Y)=∑i=0m−1xifi(Y)=∑j=0l−1ajYj,然后使用2.1.3节中的单变量polynomial commitment argument 来evaluate A = P e d e r s e n C o m m i t ( a 0 , ⋯ , a l − 1 ) = g 0 a 0 ⋯ g l − 1 a l − 1 = g ⃗ a ⃗ A=PedersenCommit(a_0,\cdots,a_{l-1})=g_0^{a_0}\cdots g_{l-1}^{a_{l-1}}=\vec{g}^{\vec{a}} A=PedersenCommit(a0,⋯,al−1)=g0a0⋯gl−1al−1=ga to f ( x , y ) f(x,y) f(x,y) at y y y。
因此, e v a l = f ( x , y ) eval=f(x,y) eval=f(x,y) 具有 MIPP argument + 单变量polynomial evaluation argument的soundness。
3.2 structured版本的双变量polynomial commitment
为了evaluate a polynomial commitment T T T to e v a l = f ( x , y ) eval=f(x,y) eval=f(x,y):
- Prover首先计算 A = ∏ i = 0 m − 1 A i x i ∈ G 1 A=\prod_{i=0}^{m-1}A_i^{x^i}\in\mathbb{G}_1 A=∏i=0m−1Aixi∈G1,其中 A i = K Z G C o m m i t ( a i , 0 , ⋯ , a i , l − 1 ) = g 0 a i , 0 ⋯ g l − 1 a i , l − 1 = g ∑ j = 0 l − 1 a i , j α j A_i=KZGCommit(a_{i,0},\cdots,a_{i,l-1})=g_0^{a_{i,0}}\cdots g_{l-1}^{a_{i,l-1}}=g^{\sum_{j=0}^{l-1}a_{i,j}\alpha^j} Ai=KZGCommit(ai,0,⋯,ai,l−1)=g0ai,0⋯gl−1ai,l−1=g∑j=0l−1ai,jαj。
- Prover需要证明 A A A的计算是正确的,可采用2.2.2节的MIPP argument来证明。
- 接下来Prover计算polynomial f ( x , Y ) = ∑ i = 0 m − 1 x i f i ( Y ) = ∑ j = 0 l − 1 a j Y j f(x,Y)=\sum_{i=0}^{m-1}x^if_i(Y)=\sum_{j=0}^{l-1}a_jY^j f(x,Y)=∑i=0m−1xifi(Y)=∑j=0l−1ajYj,然后使用2.2.3节中的单变量polynomial commitment argument 来evaluate A = g 0 a 0 ⋯ g l − 1 a l − 1 = g ∑ j = 0 l − 1 a j α j A=g_0^{a_0}\cdots g_{l-1}^{a_{l-1}}=g^{\sum_{j=0}^{l-1}a_j\alpha^j} A=g0a0⋯gl−1al−1=g∑j=0l−1ajαj to f ( x , y ) f(x,y) f(x,y) at y y y。
因此, e v a l = f ( x , y ) eval=f(x,y) eval=f(x,y) 具有 MIPP argument + 单变量polynomial evaluation argument的soundness。
4. 单变量polynomial commitment 转换为双变量polynomial commitment
因为可将polynomial f ( X , Y ) f(X,Y) f(X,Y) 以矩阵形式表示为:【a polynomial of degree m − 1 m-1 m−1 in X X X and l − 1 l-1 l−1 in Y Y Y.】
f ( X , Y ) = ( 1 , X , X 2 , ⋯ , X m − 1 ) ( a 0 , 0 a 0 , 1 a 0 , 2 ⋯ a 0 , l − 1 a 1 , 0 a 1 , 1 a 1 , 2 ⋯ a 1 , l − 1 a 2 , 0 a 2 , 1 a 2 , 2 ⋯ a 2 , l − 1 ⋮ ⋱ ⋮ a m − 1 , 0 a m − 1 , 1 a m − 1 , 2 ⋯ a m − 1 , l − 1 ) ( 1 Y Y 2 ⋯ Y l − 1 ) = ( 1 , X , X 2 , ⋯ , X m − 1 ) A ( 1 Y Y 2 ⋯ Y l − 1 ) f(X,Y)=(1,X,X^2,\cdots,X^{m-1})\begin{pmatrix} a_{0,0} & a_{0,1} & a_{0,2} & \cdots & a_{0,l-1}\\ a_{1,0} & a_{1,1} & a_{1,2} & \cdots & a_{1,l-1}\\ a_{2,0} & a_{2,1} & a_{2,2} & \cdots & a_{2,l-1}\\ \vdots & & & \ddots & \vdots\\ a_{m-1,0} & a_{m-1,1} & a_{m-1,2} & \cdots & a_{m-1,l-1} \end{pmatrix} \begin{pmatrix} 1\\ Y\\ Y^2\\ \cdots \\ Y^{l-1} \end{pmatrix}=(1,X,X^2,\cdots,X^{m-1})\mathcal{A}\begin{pmatrix} 1\\ Y\\ Y^2\\ \cdots \\ Y^{l-1} \end{pmatrix} f(X,Y)=(1,X,X2,⋯,Xm−1)⎝⎜⎜⎜⎜⎜⎛a0,0a1,0a2,0⋮am−1,0a0,1a1,1a2,1am−1,1a0,2a1,2a2,2am−1,2⋯⋯⋯⋱⋯a0,l−1a1,l−1a2,l−1⋮am−1,l−1⎠⎟⎟⎟⎟⎟⎞⎝⎜⎜⎜⎜⎛1YY2⋯Yl−1⎠⎟⎟⎟⎟⎞=(1,X,X2,⋯,Xm−1)A⎝⎜⎜⎜⎜⎛1YY2⋯Yl−1⎠⎟⎟⎟⎟⎞
于是,polynomial f ( X , Y ) = ∑ i = 0 m − 1 f i ( Y ) X i f(X,Y)=\sum_{i=0}^{m-1}f_i(Y)X^i f(X,Y)=∑i=0