ACKRec:注意力异构图卷积深度知识推荐器 SIGIR 2020

论文链接:http://keg.cs.tsinghua.edu.cn/jietang/publications/Sigir20-Gong-et-al-MOOC-concept-recommendation.pdf
摘要
大规模的在线公开课程(MOOC)正在成为一种流行的教育方式,为学生掌握知识提供了大规模的开放式学习机会。为了吸引学生的兴趣,MOOC提供商使用推荐系统向学生推荐课程。但是,由于一门课程通常包含许多视频讲座,每个讲座都涵盖一些特定的知识概念,因此直接推荐课程会忽略学生对某些特定知识概念的兴趣。为了填补这一空白,本文研究了知识概念推荐的问题。对于MOOC中的知识概念推荐,我们提出了一种基于端到端图神经网络的方法,称为注意力异构图卷积深度知识推荐器(ACKRec)。像其他推荐问题一样,它也遇到了稀疏问题。为了解决这个问题,我们利用内容信息和上下文信息来通过图卷积网络学习实体的表示。除了学生和知识概念,我们考虑其他类型的实体(例如,课程,视频,教师),并构建异构信息网络(HIN),以捕获不同类型的实体之间相应的卓有成效的语义关系,并将其纳入表示学习过程。具体来说,我们在HIN上使用元路径来指导学生偏好的传播。借助这些元路径,可以获取有关候选知识概念的学生偏好分布。此外,我们提出了一种注意力机制,以自适应地融合来自不同元路径的上下文信息,以捕获不同学生的不同兴趣。为了学习所提出模型的参数,我们提出利用扩展矩阵分解(MF)。进行了一系列实验,与最先进的基准方法相比,它展示了ACKRec在多种流行指标上的有效性。实验结果表明,提出的ACKRec能够有效地向在MOOC中寻求在线学习的学生推荐知识概念。
1、本文贡献
本文的主要贡献可以概括如下:
- 我们确定了知识概念推荐的重要问题,而现有的MOOC推荐系统常常忽略了这一问题。知识概念推荐填补了这一空白,并提供了更多的微观的建议。
- 我们提出了ACKRec,这是一种新颖的端到端框架,它利用丰富的异构上下文辅助信息来辅助知识概念的推荐。
- 我们开发了异构信息网络建模,以捕获MOOC平台中不同类型实体之间的各种复杂交互。
- 我们设计了一个基于注意力的图卷积网络,该网络可以将内容和异构上下文合并到不同实体的表示学习中。该模型可以在元路径的指导下传播用户的偏好来自动发现用户的潜在兴趣。
- 我们使用从XuetangX收集的真实数据进行了大量实验研究,以全面评估所提出模型的性能。我们研究了参数,包括元路径组合,表示维度,潜在因素个数和GCN层数。证明了所提出模型与一系列严格基准相比的有效性。
2、问题定义与模型框架
2.1、问题定义
给定目标用户在MOOC中的交互式数据,目标是计算有关用户和一系列知识概念的兴趣分数,然后推荐评分前 N N N高的知识概念列表。 具体地,给定用户 u u u的交互数据,一个预测函数 f f f被学习并用于生成知识概念 K K K的推荐列表(例如“ c ++”,“二叉树”,“链表”等),使得 f : u → { k i ∣ k i ∈ K , i < N } f:u\to\{k_i|k_i\in K,i
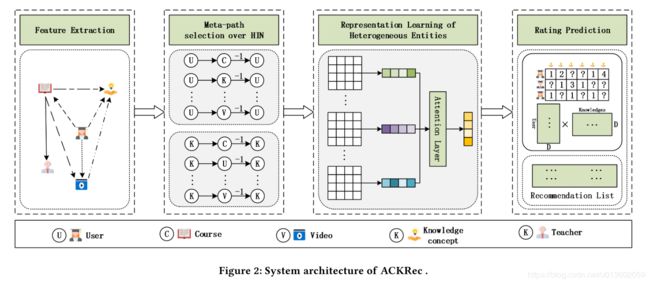
2.2、模型框架
- Feature Extraction. 通过使用从MOOC中收集的数据,我们首先从知识概念的名称中提取内容信息作为内容特征,然后分析各种关系(例如,concept-vidio和concept-course)和不同类型的实体(例如知识概念 ,视频,课程)来描述知识概念。 同样,我们还为用户生成概念特征和上下文特征。
- Meta-path Selection. 基于从数据中提取的特征,在该模块中,我们构建结构化的HIN来建模不同类型实体之间的关系,然后从HIN中选择不同的元路径(即具有不同含义)来描述知识概念的相关性。 例如,如果两个不同的用户注册了同一门课程,我们将在两个用户之间建立一条边。
- Representation Learning of Heterogeneous Entities. 基于上一步构建的元路径,提出了一种表示学习模型,以学习异质视图中实体的低维表示。 该模型能够捕获异构实体之间的结构相关性。 具体来说,我们利用选定的元路径通过图卷积网络来指导实体表示学习。 然后,我们利用注意力机制自适应地融合了来自不同元路径的学习到的实体表示。
- Rating Prediction. 在生成用户和知识概念的低维表示之后,实体的密集向量被馈送到扩展矩阵分解中以学习模型的参数。 此外,我们根据用户-项目(学生-知识概念)评级矩阵来预测用户对未点击知识概念的兴趣。
3、ACKRec模型
3.1、Feature Extraction
3.1.1、Content Feature
使用Word2vec方法得到知识概念(例如:C++,二叉树,链表)和用户的内容表示。
3.1.2、Context Feature
诸如知识概念名称的单词嵌入之类的内容特征可以用于表示知识概念的信息。 此外,还存在丰富的上下文信息,例如网络结构中不同实体之间的关系(例如,用户:207256观看的视频:v_9e77179和视频:v_1a9aa686;此行为暗含了两个视频之间的关系)。 为了在不同类型的实体之间包括这些复杂的关系,我们进一步将上下文信息建模为特征。 具体来说,我们在用户学习活动中考虑以下关系。
- R 1 u R_1^u R1u:构建user-click-knowledge concept 矩阵 A 1 u A_1^u A1u,矩阵中的每一个元素 c i , j ∈ { 0 , 1 } c_{i,j}\in\{0,1\} ci,j∈{0,1},表明一个用户 i i i在学习过程中是否点击了知识概念 j j j。
- R 2 u R_2^u R2u:构建user-learn-course矩阵 A 2 u A_2^u A2u,矩阵中的每个元素 l i , j ∈ { 0 , 1 } l_{i,j}\in\{0,1\} li,j∈{0,1},表明一个用户 i i i是否学习过课程 j j j。
- R 3 u R_3^u R3u:构建user-watch-video矩阵 A 3 u A_3^u A3u,矩阵中的每个元素 w i , j ∈ { 0 , 1 } w_{i,j}\in\{0,1\} wi,j∈{0,1},表明一个用户 i i i是否看过视频 j j j。
- R 4 u R_4^u R4u:构建user-learn-course-taught by-teacher矩阵 A 4 u A_4^u A4u,矩阵中的每个元素 t i , j ∈ { 0 , 1 } t_{i,j}\in\{0,1\} ti,j∈{0,1},表明一个用户 i i i学习过老师 j j j教的课程。
除了以上的用户交互数据之外,我们还构建了知识实体之间的关系,例如:knowledge concept-included by-video和knowledge concept-involved-course等。
3.2、Meta-path Based Relationship
首先定义了网络模式,即异构网络 G \mathcal{G} G的一个子集 S \mathcal{S} S,如下图所示:
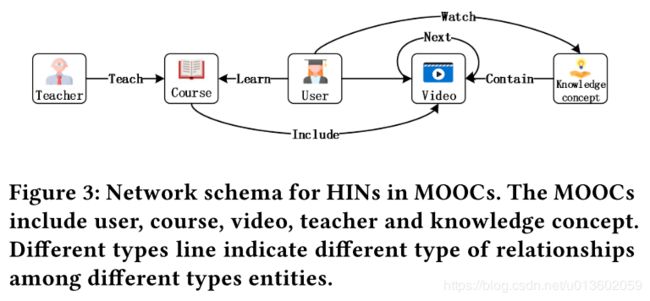
元路径meta-path:
- U ⟶ c l i c k K ⟶ c l i c k − 1 U U\stackrel{click}{\longrightarrow}K\stackrel{click^{-1}}{\longrightarrow}U U⟶clickK⟶click−1U表示两个不同的用户点击过相同的知识概念。
- U ⟶ l e a r n C ⟶ t a u g h t b y T ⟶ t a u g h t b y − 1 C ⟶ l e a r n − 1 U U\stackrel{learn}{\longrightarrow}C\stackrel{taught\space by}{\longrightarrow}T\stackrel{taught\space by^{-1}}{\longrightarrow}C\stackrel{learn^{-1}}{\longrightarrow}U U⟶learnC⟶taught byT⟶taught by−1C⟶learn−1U表示两个不同的用户学习过同一个老师教的课程。
3.3、Attention-based Graph Convolutional Networks for HIN Representation Learning
在得到内容信息和上下文信息的向量表示之后,我们将实体内容信息输入到图卷积网络GCN中来学习实体的表示。给定一个异质信息网络 G = ( V , E ) \mathcal{G}=(\mathcal{V},\mathcal{E}) G=(V,E)和一系列元路径的集合 M P = { M P 1 , M P 2 , ⋯ , M P ∣ M P ∣ } \mathcal{MP}=\{MP_1,MP_2,\cdots,MP_{|MP|}\} MP={MP1,MP2,⋯,MP∣MP∣},以及每条元路径对应的邻接矩阵 A = { A 1 , A 2 , ⋯ , A M P } \mathcal{A}=\{A_1,A_2,\cdots,A_{MP}\} A={A1,A2,⋯,AMP},这里 ∣ M P ∣ |MP| ∣MP∣代表元路径的条数。我们采用多层GCN来学习实体的表示: h ( l + 1 ) = σ ( P h l W l ) h^{(l+1)}=\sigma\left(Ph^lW^l\right) h(l+1)=σ(PhlWl)其中 l l l代表第 l l l层GCN, h 0 h^0 h0表示在第一步提取到的内容特征, P = D ~ − 1 2 A ~ D ~ − 1 2 P=\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} P=D~−21A~D~−21, A ~ = A + I \tilde{A}=A+I A~=A+I, D ~ = diag ( A ~ 1 ) \tilde{D}=\text{diag}(\tilde{A}\textbf{1}) D~=diag(A~1),这里 1 \textbf{1} 1表示全1的向量。
这里,我们设定 P 0 = P 1 = P 2 = D ~ − 1 2 A ~ D ~ − 1 2 P^0=P^1=P^2=\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} P0=P1=P2=D~−21A~D~−21,并使用3层GCN来获得实体的表示: h 1 = R e L U ( ( P 0 X ) W 0 ) h^1=ReLU((P^0X)W^0) h1=ReLU((P0X)W0) h 2 = R e L U ( ( P 1 H 1 ) W 1 ) h^2=ReLU((P^1H^1)W^1) h2=ReLU((P1H1)W1) h 3 = R e L U ( ( P 2 H 2 ) W 2 ) h^3=ReLU((P^2H^2)W^2) h3=ReLU((P2H2)W2) e M P = h 3 e_{MP}=h^3 eMP=h3,我们选取 e M P ∈ R d e_{MP}\in\mathbb{R}^d eMP∈Rd作为实体的最终表示。但是不同的元路径应当有不同的权重,即: e = ∑ i = 1 ∣ M P ∣ a t t ( e M P i ) e M P i e=\sum_{i=1}^{|MP|}att(e_{MP_i})e_{MP_i} e=i=1∑∣MP∣att(eMPi)eMPi在此问题中,我们主要关注用户和知识概念这两种实体,给定每一条元路径的表示 e M P i e_{MP_i} eMPi之后,我们定义每条元路径的权重公式如下: α M P i = e x p ( σ ( a e M P i ) ) ∑ j ∈ ∣ M P ∣ e x p ( σ ( a e M P i ) ) \alpha_{MP_i}=\frac{exp(\sigma(ae_{MP_i}))}{\sum_{j\in|MP|}exp(\sigma(ae_{MP_i}))} αMPi=∑j∈∣MP∣exp(σ(aeMPi))exp(σ(aeMPi))
3.4、Matrix Factorization for Knowledge Concept Recommendation
在得到以上的信息表示之后,我们提出一种扩展的矩阵分解方法,这里选取用户点击知识点作为评分矩阵,一个用户对一个知识点的评分计算如下: r u , k ^ = x u ⊤ y k \hat{\textbf{r}_{u,k}}=\textbf{x}_u^{\top}\textbf{y}_k ru,k^=xu⊤yk这里, x u ∈ R D × m \textbf{x}_u\in\mathbb{R}^{D\times m} xu∈RD×m和 y k ∈ R D × n \textbf{y}_k\in\mathbb{R}^{D\times n} yk∈RD×n分别代表用户的潜在因素表示和知识点的潜在因素表示。由于我们已经得到了用户和知识点的表示,因此,我们将公式扩展为: r u , k ^ = x u ⊤ y k + β u ⋅ e u ⊤ t k + β k ⋅ t u ⊤ e k \hat{\textbf{r}_{u,k}}=\textbf{x}_u^{\top}\textbf{y}_k+\beta_u\cdot\textbf{e}^{u\top}\textbf{t}^k+\beta_k\cdot\textbf{t}^{u\top}\textbf{e}^k ru,k^=xu⊤yk+βu⋅eu⊤tk+βk⋅tu⊤ek这里 t u \textbf{t}^u tu和 t k \textbf{t}^k tk为训练参数使得 e u \textbf{e}^u eu和 e k \textbf{e}^k ek在相同的隐空间中。最终的损失函数为: m i n U , K 1 m × n ∑ u = 1 n ∑ k = 1 m ( r u , k − r u , k ^ ) 2 + λ ( ∣ ∣ x u ∣ ∣ 2 + ∣ ∣ y k ∣ ∣ 2 + ∣ ∣ t u ∣ ∣ 2 + ∣ ∣ t k ∣ ∣ 2 ) min_{U,K}\frac{1}{m\times n}\sum_{u=1}^n\sum_{k=1}^m(\textbf{r}_{u,k}-\hat{\textbf{r}_{u,k}})^2+\lambda\left(||\textbf{x}_u||^2+||\textbf{y}_k||^2+||\textbf{t}^u||^2+||\textbf{t}^k||^2\right) minU,Km×n1u=1∑nk=1∑m(ru,k−ru,k^)2+λ(∣∣xu∣∣2+∣∣yk∣∣2+∣∣tu∣∣2+∣∣tk∣∣2)
4、实验
数据集信息如下:
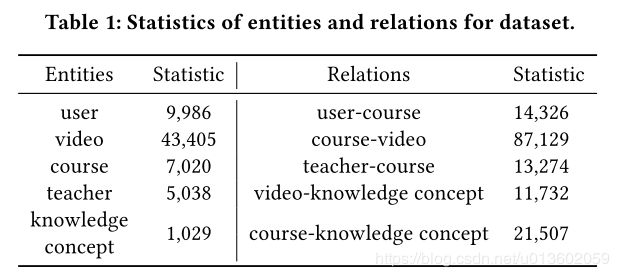
不同元路径下的组合实验结果如下图所示:

其中:
- M P 1 MP_1 MP1: U → K ⟶ − 1 U U\to K\stackrel{-1}{\longrightarrow}U U→K⟶−1U
- M P 2 MP_2 MP2: U → C ⟶ − 1 U U\to C\stackrel{-1}{\longrightarrow}U U→C⟶−1U
- M P 3 MP_3 MP3: U → V ⟶ − 1 U U\to V\stackrel{-1}{\longrightarrow}U U→V⟶−1U
- M P 4 MP_4 MP4: U → C → T ⟶ − 1 C ⟶ − 1 U U\to C\to T\stackrel{-1}{\longrightarrow}C \stackrel{-1}{\longrightarrow} U U→C→T⟶−1C⟶−1U
不同的潜在因素个数与嵌入维度对实验结果的影响:
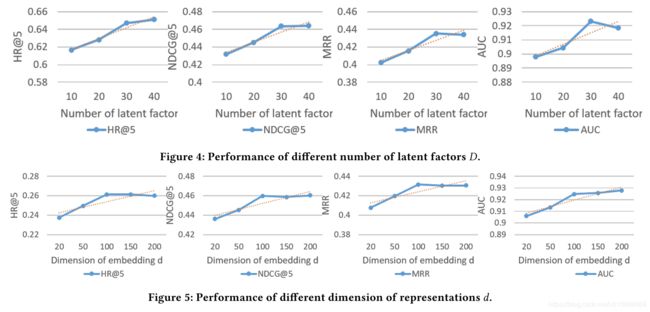
不同的对比方法下的实验结果:

不同的GCN层数对实验结果的影响:

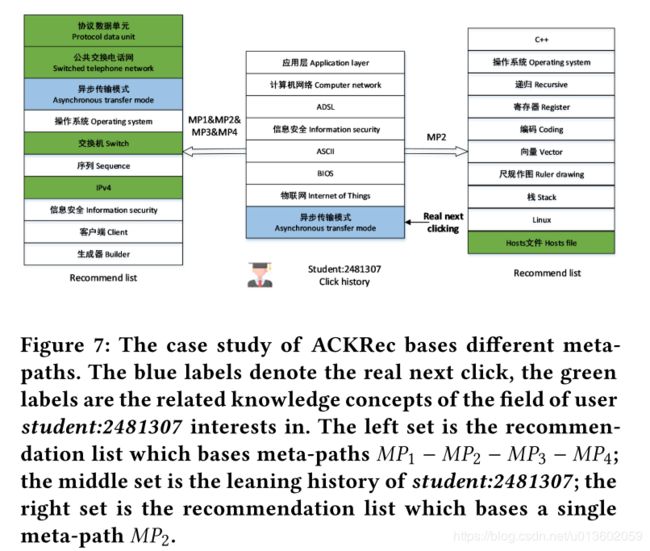
case study: