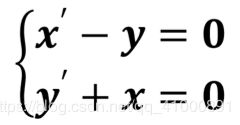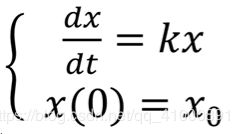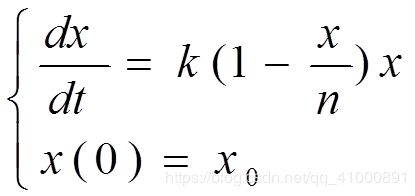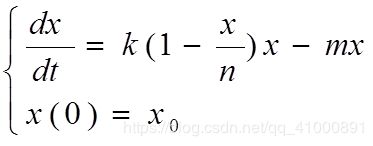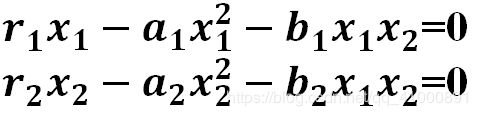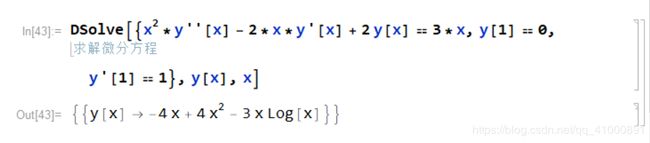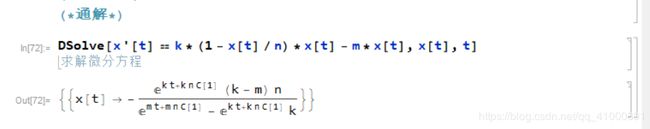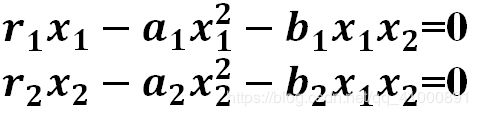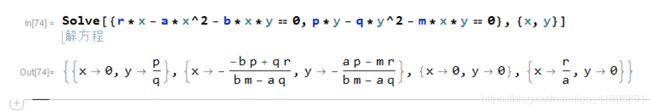mathematica动态模型的建模分析
题目
1、动态模型的建模分析,写出求解过程及分析结论。
(1)求解微分方程y'-xy=3x
(2)求微分方程x2y''-2xy'+2y=3x满足条件y(1)=0,y'(1)=1的特解。
(3)求微分方程组的通解。
(4)求函数f(x)=x3-4x+3在区间[-2,2]的极值。
(5)已知一组数据(-1,2),(0,2.5),(1,3),(2,4),(3,4.5),(4,5.5),求已知数据的拟合函数。
(6)应用Mathematica求解传染病模型,模型Ⅰ(指数模型)的通解与特解,并绘图。
(7)应用Mathematica求解传染病模型,模型Ⅱ(阻滞模型,SI模型),的通解与特解,并绘图(三种形状: S形状,正态形状,钟形)。
(8)应用Mathematica求解传染病模型,模型Ⅲ(SIS模型),的通解与特解。
(9)课程第7讲中的问题。在一片没有管理的林区,硬材树与软材树竞争可用的土地和水分。越可用的硬材树生长得越慢。软材树靠生长快、有效消耗水分和土壤养分与硬材树竞争。硬材树靠生长的高度与软材树竞争,它们遮挡了小树的阳光,也更抗疾病。这两种树能否同时在一片林区中无限期地共存,或者一种树是否会迫使另一种树灭绝?应用Mathematica求解以下方程。分析问题。
2、写出简短程序,绘制特殊图形
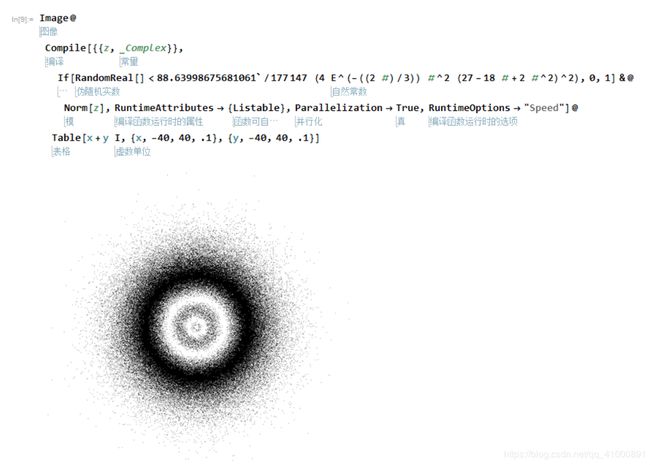
(1)在Mathematica中绘制如下的星空图。
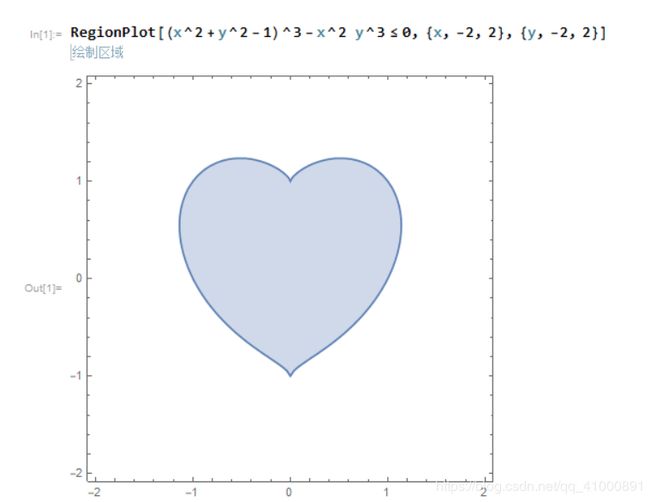
(2)在Mathematica中绘制心形图。提示:心形曲线的方程为,r=a(1-sinθ)
(3)在Mathematica中绘制三叶草或四叶草的图形。
(4)在Mathematica中绘制瓶子或罐子。
(5)在Mathematica中绘制海螺。
(6)在Mathematica中绘制魔方。
(7)在Mathematica中绘制漫画人形图。
(8)绘制其它任何,你觉得有意思的图形,现实存在的,或幻想的,或未来的图形。
解答过程
1、动态模型的建模分析
(1)根据题目一要求,输入微分方程,通过DSolve命令得到微分方程求解结果如下图所示:
图 1 - 微分方程求解
(2)根据题目二要求,输入微分方程,通过DSolve命令得到微分方程特解结果如下图所示:
图 2 - 微分方程特解
(3)根据题目三的要求,输入微分方程组,通过DSolve命令求得微分方程组的特解如下图所示:
图 3 - 微分方程组求特解
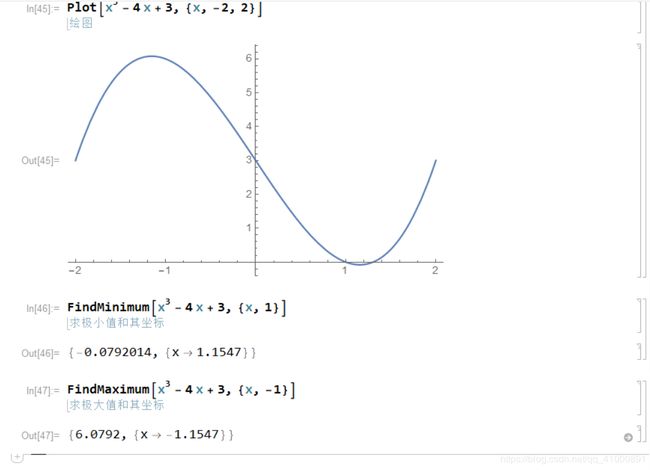
(4)根据题目四的要求,通过Plot和求极值命令得到函数在[-2,2]上的极值如下图所示:
图 4 - 求函数极值
(5)根据题目五的要求,通过Fit和Plot等函数命令得到改组数据的拟合数据,计算过程如下图所示:
首先求数据拟合
图 5 - 求数据拟合
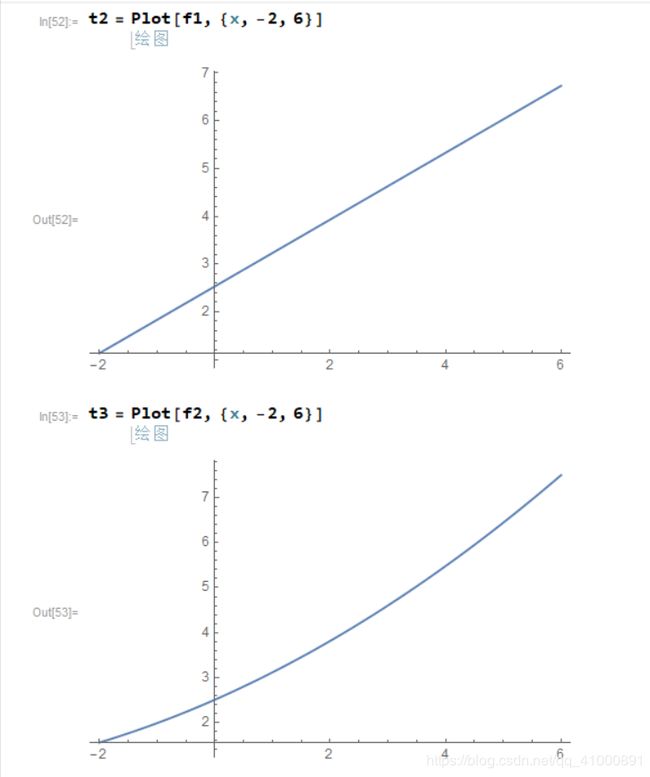
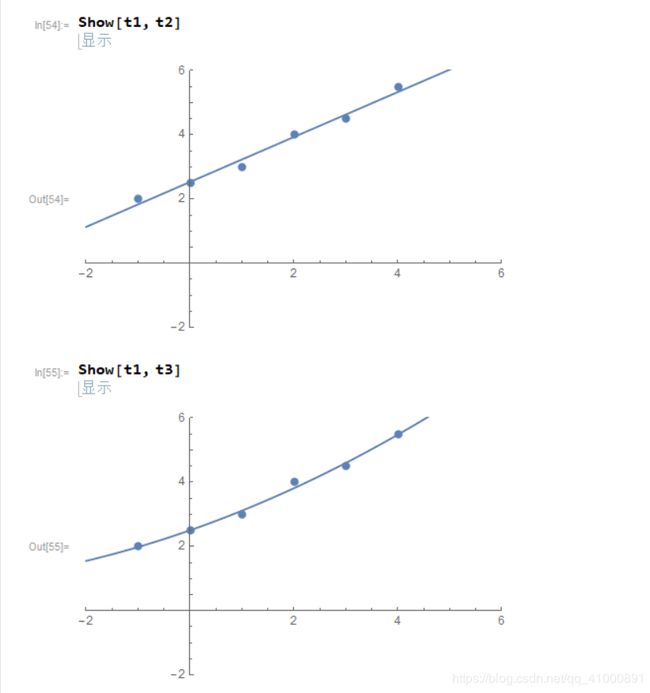
Plot和Show等命令画出数据的散点图以及相关拟合的函数图像进行比较,比较结果如下图所示
图 6 - Plot作图
同时可以通过Show[图形变量组,可选项]的形式,将多个函数的图像画在同 一坐标系中,绘制结果如下图所示:
图 7 - Show作图
根据绘制结果分析,可以发现第二次比第一次的拟合程度高,但从简单实用的角度,可以选择第一个拟合函数
(6)根据题目六的要求,利用mathematica求解传染病模型,求解器通解和特解,并绘制图案。
通过计算可以的到通解和特解分别如下图所示:
图 8 - 通解和特解
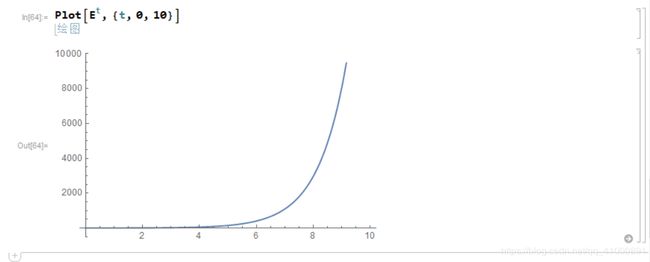
绘制图案,将a=1,k=1如下图所示:
图 9 - 绘制图案
(7)根据题目七的要求,利用mathematica求解传染病模型2,求得其通解和特解,并绘制三种图案。
通过计算可以的到通解和特解分别如下图所示:
图 10 - 通解和特解
绘制图案,将a=1,k=1如下图所示:
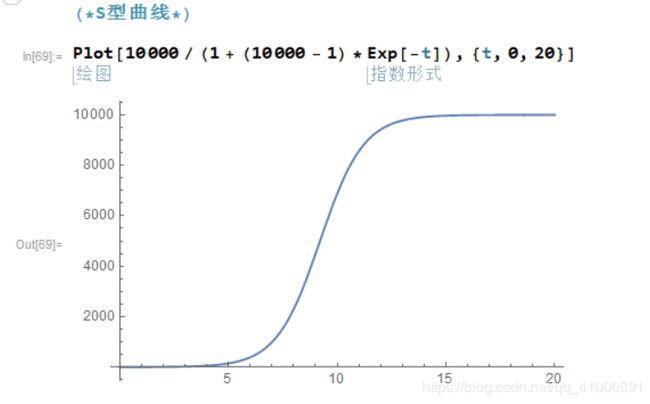
S型曲线:
图 11 - S型曲线
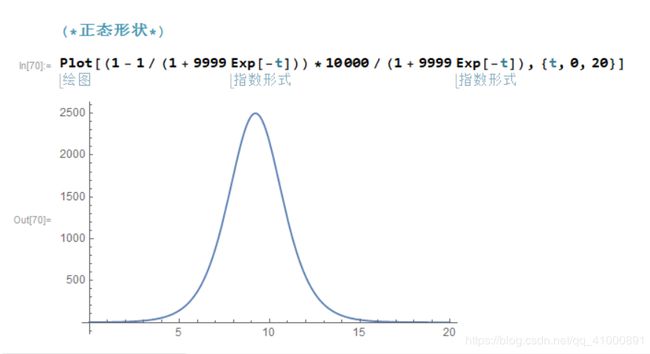
正态形状:
图 12 - 正态形状
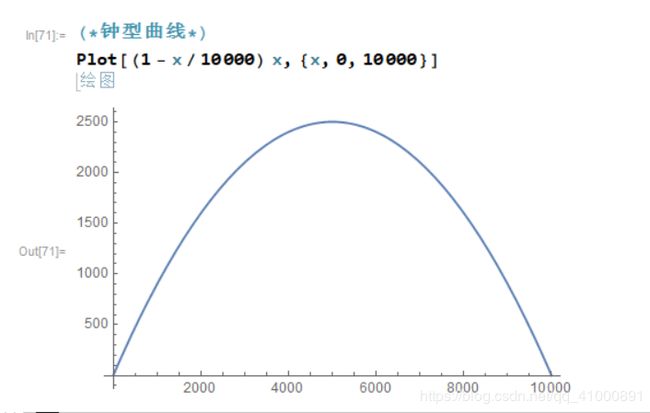
钟型曲线:
图 13 - 钟型曲线
(8)根据题目八的要求,利用mathematica求解传染病模型Ⅲ,求得其通解和特解,得到结果如下图所示:
图 14 - 通解求解
(9)根据题目九的要求,利用mathematica求解下列方程:
通过求解得到结果如下图所示:
图 15 - 求解方程
2、写出简短程序,绘制特殊图形
(1)通过查阅相关资料,根据题目要求画氢原子电子云((n,m,l)=(4,0,3))示意图,利用Mathematica绘制可得到近似于星空图如下:
图 16 - 星空图绘制
(2)在Mathematica中绘制心形图。根据心形曲线的方程为,r=a(1-sinθ)绘制得到心形图如下:
图 17 - 心形图绘制
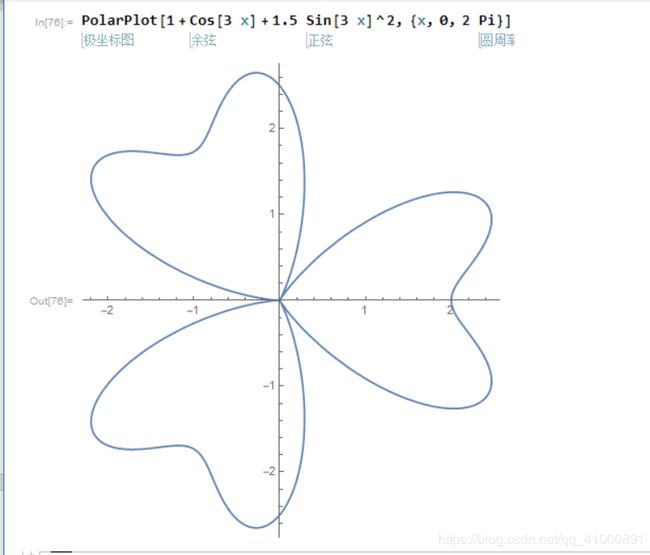
(3)三叶草曲线
首先确定极坐标方程为r(x)=1+cos(3x)+1.5×[sin(3x)]^2,范围为[0,2π],使用PolarPlot命令在Mathematica即可绘制一个相比官方实例较为复杂的三叶草曲线,绘制图案如下图所示:
图 18 - 三叶草曲线
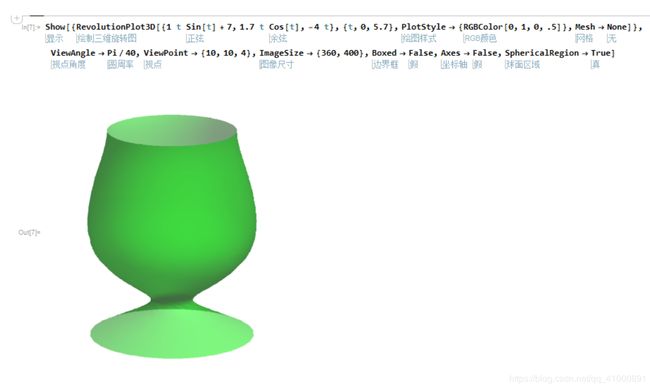
(4)在Mathematica中绘制瓶子或罐子。
通过查阅资料,通过Manipulate使用RevolutionPlot3D三维旋转图命令得到一个花瓶,生成花瓶如下:
图 19 - 花瓶绘制
(5)在Mathematica中绘制海螺。
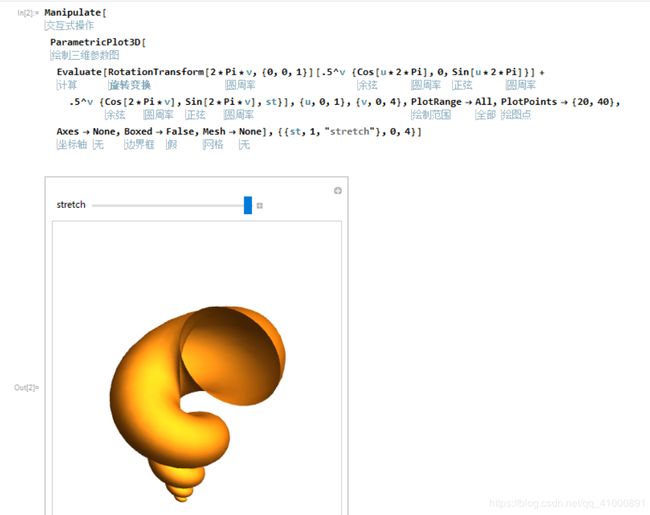
通过查阅资料,通过Manipulate使用交互操作得到一个可以变形得到海螺的命令,并生成海螺如下:
图 20 - 绘制海螺图
(6)在Mathematica中绘制魔方。
通过查阅资料,通过Manipulate利用三维图像,数组等知识,绘制魔方如下图所示:
图 21 - 魔方绘制
(7)在Mathematica中绘制漫画人形图。
图 22 - 绘制人形图
(8)绘制其它任何,你觉得有意思的图形,现实存在的,或幻想的,或未来的图形。
图 23 - 绘制随意图案