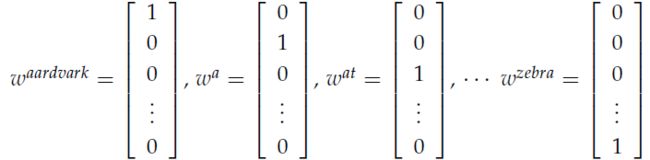NLP-CS224n学习讲义PART 1——Word Vector 1: Introduction, SVD and Word2vec
1 介绍NLP
1.1 NLP有什么特别之处?
人类的语言是一个专门用来传达意思的系统,而不是由任何一种物质表现所产生的。在这方面,它与视觉或其他任何机器学习任务有很大区别。
大多数单词只是语言外实体的符号,而语言符号可以被编码成多种形式,比如声音、手势、文字等连续的信号。
1.2 NLP任务举例
从语音处理到语义解释和语篇处理,自然语言处理任务的level是不同的。不同level如下:
简单:
- 拼写检查
- 关键词搜索
- 同义词搜索
中等:
- 解析来自网站、文档等的信息
困难:
- 机器翻译(英译汉)
- 语义分析(查询语句的意思)
- 共指关系(比如“他”或“它”指的是否为给定的文档)
- 问题回答
1.3 如何表示单词
所有NLP的首要任务是要将单词转换为能够放到计算机模型的一种输入表示。许多早期的NLP工作将单词视为原子符号。
为了在大多数NLP任务中能够得到良好的性能,我们首先需要对单词之间的相似性和差异性有一些概念。那么我们可以使用word vectors,有了这些vectors,那么words之间的相似性和差异就能很好的表示出来了(比如使用Jaccard, Cosine, 欧拉距离等衡量),为什么呢?我们接下来仔细谈。
2 Word Vectors
上面说到有了word vectors,那么words之间的相似性和差异就能很好的表示出来。所以接下来主要认识一下NLP中非常核心的知识——Word Vectors。
我们知道世界上英语单词的数量是及其巨大的,但这些单词与单词之间难道就没有什么关联吗?很明显是有的,比如Friday和Wednesday之间就有“周几”的一个关联,还比如hotel和motel都有旅店的意思,所以是相似的。因此为了表示这种单词之间的关联,我们希望能够将单词编码成向量表示,从而可以表示为一个空间中的某个点(这样点与点之间就可以通过距离进行衡量了是吧)
最简单也非常常用的编码表示就是one-hot vector:将每个单词表示为一个 R ∣ V ∣ × 1 R^{|V|\times1} R∣V∣×1向量, ∣ V ∣ |V| ∣V∣表示字典中词汇的个数。如果这个单词排第一个,则 r 1 = 1 r_1 = 1 r1=1,其余全为0。
但是这种表示方式的缺点就是不能够直接显示单词的相似性,比如hotel和motel其实是相似的,但是相乘之后得到0,,完全不能够知道它们之间有什么关联吧。
3 基于SVD的方法
首先,我们介绍一下SVD,即大名鼎鼎的奇异值分解。一个矩阵X可以分解为 U S V T USV^T USVT,然后我们使用 U U U的行数作为字典中单词的嵌入维数。说到奇异值分解,就有一种机器学习方法往往与其密切相关,即降维,而单词的嵌入不就是降维嘛。
3.1 Word-Document矩阵
我们可以有一个猜测:相似的单词往往会出现在相同的文档中,所以可以根据这个猜测构建一个Word-Document矩阵,构建方式如下:循环遍历数十亿个文档,每当文档 j j j中出现了单词 i i i,我们就在条目 X i j X_{ij} Xij中加一。
3.2 基于Window的Co-occurrence矩阵
初看这里的Co-occurrence我是不明白什么意思的,翻译为“同现关系、词汇同现”,在这个方法中,我们计算每个单词在一个特定大小的窗口中出现的次数。举个文档中的例子就明白了,我们有如下的句子:
- I enjoy flying.
- I like NLP.
- I like deep learning.
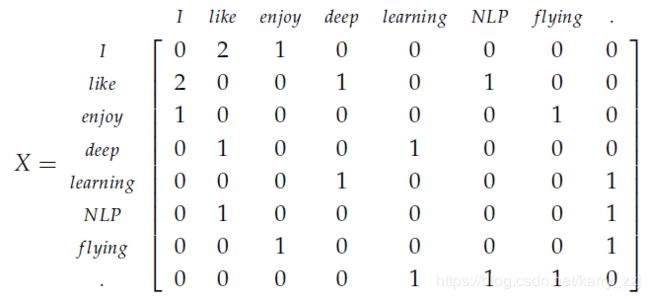
也就是说I与enjoy相邻出现的次数是1,而与like相邻出现的次数是2,那么最后的矩阵如下所示:
3.3 使用SVD进行词汇嵌入
可由上面两种方式得到的矩阵,接下来我们进行真正的奇异值分解,从而进行降维。具体SVD的方法推荐这位博主的文章:奇异值分解(SVD)原理详解及推导
对 X X X运用SVD之后,选择前k个奇异向量进行降维,这样就得到了k维的词向量。
4 基于迭代的方式——Word2vec
上面我们整理的主要是一种需要存储全局信息的方法,而这个对于庞大的语言数据是具有非常大的挑战的。我们能否局部进行学习,即根据某个词汇的上下文(context)来编码这个词的出现概率。
那么接下来进入NLP中非常重要的方法——Word2vec,我们可以试图顾名思义一下,就是说这个方法涉及到两种单词的向量,那这两种单词是什么呢?上面提到想要通过某个词汇的上下文进行局部学习,那么可以猜想这两种单词就是当前单词和与其邻近的单词。
具体而言,Word2vec是一种软件包,其包括:
- 2种算法:continuous bag-of-words(CBOW)和skip-gram
- 2种训练方式:negative sampling和hierarchical softmax
4.1 语言模型(Unigrams, Bigrams等)
对于一个句子的合理性,我们可以通过概率来表示,如果一个句子中含有n个单词即序列 w 1 , w 2 , . . . , w n w_1, w_2, ..., w_n w1,w2,...,wn,那么概率 P ( w 1 , w 2 , . . . , w n ) P(w_1, w_2, ..., w_n) P(w1,w2,...,wn) 的大小就表示此句子的合理性。如果假定单词之间的出现是完全独立的,那么
P ( w 1 , w 2 , . . . , w n ) = ∏ i = 1 n P ( w i ) P(w_1, w_2, ..., w_n) = \prod_{i=1}^nP(w_i) P(w1,w2,...,wn)=∏i=1nP(wi)
但这是不切实际的,因为相邻的单词之间明显是有联系的,并不是独立的,所以可以让这个序列的概率依赖于序列中一个单词及其旁边的单词的成对概率,那么
P ( w 1 , w 2 , . . . , w n ) = ∏ i = 2 n P ( w i ∣ w i − 1 ) P(w_1, w_2, ..., w_n) = \prod_{i=2}^nP(w_i|w_{i-1}) P(w1,w2,...,wn)=∏i=2nP(wi∣wi−1)
4.2 Continuous Bag-of-Words(CBOW)
核心思想是根据上下文词来预测中心词。比如给定上下文词汇{“The”, “cat”, ’over", “the’, “puddle”},我们来预测其中心词"jumped”。下面一张图也非常的直观,而连续的词袋意思就是上下文对应的词有8个,前后各4个,这8个词相当于在一个“袋子”中。
算法过程如下:
首先我们需要创建两个矩阵 V ∈ R n × ∣ V ∣ , U ∈ R ∣ V ∣ × n V\in R^{ n\times|V|},U \in R^{ |V|\times n} V∈Rn×∣V∣,U∈R∣V∣×n,n表示单词嵌入空间的维数, V V V是用来词汇嵌入的,相应的 $ U$是用来词汇展开的(展开为原来one-hot的维数)。
-
首先对于大小为m的词袋,我们先产生one-hot词向量:
( x ( c − m ) , . . . , x ( c − 1 ) , x ( c + 1 ) , . . . , x ( c + m ) ∈ R ∣ V ∣ ) (x^{(c-m)}, ..., x^{(c-1)}, x^{(c+1)}, ..., x^{(c+m)} \in R^{|V|}) (x(c−m),...,x(c−1),x(c+1),...,x(c+m)∈R∣V∣)
-
我们将这些词向量嵌入到n维向量中:
。 ( v c − m = V x ( c − m ) , . . . , v c − 1 = V x ( c − 1 ) , v c + 1 = V x ( c + 1 ) , . . . , v c + m = V x ( c + m ) ∈ R n ) 。(v_{c-m} = Vx^{(c-m)}, ..., v_{c-1} = Vx^{(c-1)}, v_{c+1} = Vx^{(c+1)}, ..., v_{c+m} = Vx^{(c+m)} \in R^{n}) 。(vc−m=Vx(c−m),...,vc−1=Vx(c−1),vc+1=Vx(c+1),...,vc+m=Vx(c+m)∈Rn)
-
获得这些向量的平均向量 v ^ = v c − m + v c − m + 1 + . . . + v c + m 2 m ∈ R n \hat{v} = \frac{v_{c-m} + v_{c-m+1}+...+v{c+m}}{2m}\in R^n v^=2mvc−m+vc−m+1+...+vc+m∈Rn。
-
生成一个分数向量 z = U v ^ z = U\hat{v} z=Uv^,由于相似向量的点积比较大,为了得到高分,会把相似的单词推得很近。
-
将z转换为概率 y ^ = s o f t m a x ( z ) ∈ R ∣ V ∣ \hat{y} = softmax(z) \in R^{|V|} y^=softmax(z)∈R∣V∣。
-
我们期望 y ^ 与 y \hat{y}与y y^与y匹配,距离度量为cross entropy H ( y ^ , y ) H(\hat{y}, y) H(y^,y)。
我们最后的优化目标为:
m i n i m i z e J = − l o g P ( w c ∣ w c − m , . . . , w c − 1 , w c + 1 , . . . , w c + m ) = − l o g P ( u c ∣ v ^ ) = − l o g e x p ( u c T v ^ ) ∑ j = 1 ∣ V ∣ e x p ( u j T v ^ ) = − u c T v ^ + l o g ∑ j = 1 ∣ V ∣ e x p ( u j T v ^ ) minimize \ J \\= -logP(w_c|w_{c-m},...,w_{c-1}, w_{c+1},...,w_{c+m})\\ = -logP(u_c|\hat{v})\\=-log\frac{exp(u_c^T\hat{v})}{\sum_{j=1}^{|V|}exp(u_j^T\hat{v})}\\=-u_c^T\hat{v}+log\sum_{j=1}^{|V|}exp(u_j^T\hat{v}) minimize J=−logP(wc∣wc−m,...,wc−1,wc+1,...,wc+m)=−logP(uc∣v^)=−log∑j=1∣V∣exp(ujTv^)exp(ucTv^)=−ucTv^+log∑j=1∣V∣exp(ujTv^)
通过随机梯度SGD进行词向量 u c , v j u_c, v_j uc,vj的更新。
4.3 Skip-Gram 模型
核心思想与上面CBOW相反,即根据中心词来预测上下文词。比如给定词"jumped",我们来预测其上下文词汇{“The”, “cat”, ’over", "the’, “puddle”}。
算法过程如下:
和CBOW中一样,我们需要创建两个矩阵 V ∈ R n × ∣ V ∣ , U ∈ R ∣ V ∣ × n V\in R^{ n\times|V|},U \in R^{ |V|\times n} V∈Rn×∣V∣,U∈R∣V∣×n,n表示单词嵌入空间的维数, V V V是用来词汇嵌入的,相应的 U U U是用来词汇展开的(展开为原来one-hot的维数)。
-
首先对于给定的单词 x ∈ R ∣ V ∣ x\in R^{|V|} x∈R∣V∣,我们先产生其one-hot词向量。
-
我们将其嵌入到n维向量中: v c = V x ∈ R n v_{c} = Vx \in R^{n} vc=Vx∈Rn。
-
生成一个分数向量 z = U v c z = Uv_c z=Uvc。
-
将z转换为概率 y ^ = s o f t m a x ( z ) ∈ R ∣ V ∣ \hat{y} = softmax(z) \in R^{|V|} y^=softmax(z)∈R∣V∣。注意 y ^ c − m , . . . , y ^ c − 1 , y ^ c + 1 , . . . , y ^ c + m \hat{y}_{c-m},...,\hat{y}_{c-1},\hat{y}_{c+1},...,\hat{y}_{c+m} y^c−m,...,y^c−1,y^c+1,...,y^c+m为所观察的每个上下文单词的概率。
-
我们期望 y ^ c − m , . . . , y ^ c − 1 , y ^ c + 1 , . . . , y ^ c + m \hat{y}_{c-m},...,\hat{y}_{c-1},\hat{y}_{c+1},...,\hat{y}_{c+m} y^c−m,...,y^c−1,y^c+1,...,y^c+m与 y c − m , . . . , y c − 1 , y c + 1 , . . . , y c + m y_{c-m},...,y_{c-1},y_{c+1},...,y_{c+m} yc−m,...,yc−1,yc+1,...,yc+m匹配。
我们最后的优化目标为:
m i n i m i z e J = − l o g P ( w c − m , . . . , w c − 1 , w c + 1 , . . . , w c + m ∣ w c ) = − l o g ∏ j = 0 , j ≠ m 2 m P ( w c − m + j ∣ w c ) − l o g ∏ j = 0 , j ≠ m 2 m P ( u c − m + j ∣ v c ) = − l o g ∏ j = 0 , j ≠ m 2 m e x p ( u c − m + j T v c ) ∑ j = 1 ∣ V ∣ e x p ( u k T v c ) = − ∑ j = 0 , j ≠ m 2 m u c − m + j T v c + 2 m l o g ∑ k = 1 ∣ V ∣ e x p ( u k T v c ) minimize \ J \\= -logP(w_{c-m},...,w_{c-1}, w_{c+1},...,w_{c+m}|w_c)\\ = -log\prod_{j=0,j\neq m}^{2m}P(w_{c-m+j}|w_c)\\-log\prod_{j=0,j\neq m}^{2m}P(u_{c-m+j}|v_c)\\=-log\prod_{j=0,j\neq m}^{2m}\frac{exp(u_{c-m+j}^Tv_c)}{\sum_{j=1}^{|V|}exp(u_k^Tv_c)}\\=-\sum_{j=0, j\neq m}^{2m}u_{c-m+j}^Tv_c+2mlog\sum_{k=1}^{|V|}exp(u_k^Tv_c) minimize J=−logP(wc−m,...,wc−1,wc+1,...,wc+m∣wc)=−log∏j=0,j=m2mP(wc−m+j∣wc)−log∏j=0,j=m2mP(uc−m+j∣vc)=−log∏j=0,j=m2m∑j=1∣V∣exp(ukTvc)exp(uc−m+jTvc)=−∑j=0,j=m2muc−m+jTvc+2mlog∑k=1∣V∣exp(ukTvc)
通过随机梯度SGD来更新参数。