NLP-CS224n学习讲义PART 3——Neural Networks, Backpropagation
1 神经网络基础
从下面一张图我们可以知道为什么我们需要使用神经网络进行分类:

这张图显示了线性回归分类的局限性,也就是大部分的数据都不是线性可分的,所以我们需要非线性的分类器。而神经网络是一类具有非线性决策边界的分类器,如下图所示:

所以我们可以接下来主要学习神经网络的一些基础知识,很简单,但需要掌握。
1.1 一个神经元
一个神经元在神经网络中就是一个输入n个inputs并输出单个output的计算单元,不同的权重会输出不同的output。其中最常选择的神经元之一便是"sigmoid"或者称为"二元逻辑回归"神经元。
神经元计算公式为: a = 1 1 + e x p ( − ( w T x + b ) ) a = \frac{1}{1+exp(-(w^Tx+b))} a=1+exp(−(wTx+b))1
也可以写成如下形式: a = 1 1 + e x p ( − [ w T x b ] ⋅ [ x 1 ] ) a = \frac{1}{1+exp(-[w^Tx \ b]\cdot [x \ 1])} a=1+exp(−[wTx b]⋅[x 1])1
1.2 单层神经网络
单层神经网络即将多个神经元放到同一层,表示如下:
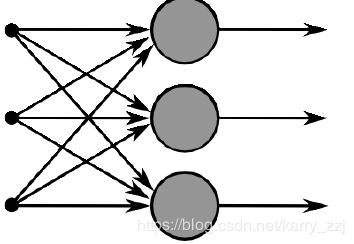
假如单层有 m m m个神经元,这样我们的权重表示为 { w ( 1 ) , . . . , w ( m ) } \{w^{(1)},...,w^{(m)}\} {w(1),...,w(m)},权重则表示为
{ b 1 , . . . , b m } \{b_1, ...,b_m\} {b1,...,bm},激活单元为 { a 1 , . . . , a m } \{a_1,...,a_m\} {a1,...,am},其中
a 1 = 1 1 + e x p ( w ( 1 ) T x + b 1 ) , . . . , a m = 1 1 + e x p ( w ( m ) T x + b m ) a_1 = \frac{1}{1+exp(w^{(1)T}x + b_1)},..., a_m = \frac{1}{1+exp(w^{(m)T}x + b_m)} a1=1+exp(w(1)Tx+b1)1,...,am=1+exp(w(m)Tx+bm)1
我们使用向量对其表示:
b = [ b 1 . . . b m ] ∈ R m b = \begin{bmatrix} b_1 \\ ... \\ b_m\end{bmatrix} \in \Bbb R^m b=⎣⎡b1...bm⎦⎤∈Rm, W = [ − w ( 1 ) T − . . . − w ( m ) T − ] ∈ R m × n W = \begin{bmatrix} - \ w^{(1)T} \ - \\ ... \\ - \ w^{(m)T} \ - \end{bmatrix} \in \Bbb R^{m\times n} W=⎣⎡− w(1)T −...− w(m)T −⎦⎤∈Rm×n
而 z = W x + b z = Wx + b z=Wx+b, 则 [ a ( 1 ) . . . a ( m ) ] = σ ( z ) = [ 1 1 + e x p ( z 1 ) . . . 1 1 + e x p ( z m ) ] \begin{bmatrix} a^{(1)} \\ ... \\ a^{(m)}\end{bmatrix} = \sigma(z) = \begin{bmatrix} \frac{1}{1+exp(z_1)} \\ ... \\ \frac{1}{1+exp(z_m)}\end{bmatrix} \quad ⎣⎡a(1)...a(m)⎦⎤=σ(z)=⎣⎡1+exp(z1)1...1+exp(zm)1⎦⎤
这些激活函数的意义就是为了非线性。
1.3 前向计算
我们上面讨论了单层神经网络计算并进行激活的过程,但这其中背后的直觉是什么呢?接下来举一个named-entity recognition问题的例子:
“Museums in Paris are amazing”
我们这里希望去识别中心词"Paris"是否为一个命名实体。在这种情况下,以便进行分类,我们可能不仅需要捕获word vectors窗口中的单词,还需要捕获单词之间的联系。我们需要另一个矩阵 U ∈ R m × 1 U \in R^{m\times 1} U∈Rm×1来为一个分类器任务从激活值来产生非标准化分数: s = U T a = U T f ( W x + b ) s = U^Ta = U^Tf(Wx + b) s=UTa=UTf(Wx+b),其中 f f f为激活函数。
1.4 Maximum Margin目标函数
最大间隔目标函数背后的思想是为了能够确保标签为"true"的数据点的分数能够比标签为"false"的数据点的分数要更高。
假定我们对于标签为"true"文本——"Museums in Paris are amazing"得到的分数记为 s s s,而把标签为"false"的文本——"Not all museums in Paris"得到分数记为 s c s_c sc,因为我们希望 s s s 要比 s c s_c sc 要高,所以我们的目标函数可能为最大化 ( s − s c ) (s-s_c) (s−sc) 或最小化 ( s c − s ) (s_c - s) (sc−s)。
我们知道如果 s > s c s > s_c s>sc,那么就没必要去优化了,所以直接为0,而如果 s c > s → s c − s > 0 s_c > s \ \rightarrow \ s_c - s > 0 sc>s → sc−s>0,那么就需要去优化,所以我们修改目标函数为:
m i n i m i z e J = m a x ( s c − s , 0 ) minimize \ J= max(s_c - s, 0) minimize J=max(sc−s,0)
然而这个目标函数是有风险的,因为它没有创建一个安全间隔 (a margin of safety)。我们的目标是让"true"得分更高,所以我们要给它加上一个正间隔 △ \bigtriangleup △,换句话说就是我们希望在 ( s − s c < △ ) → ( △ + s c − s > 0 ) (s-s_c < \bigtriangleup) \ \rightarrow \ (\bigtriangleup + s_c - s > 0) (s−sc<△) → (△+sc−s>0) 进行优化,那么目标函数修改为:
m i n i m i z e J = m a x ( △ + s c − s , 0 ) minimize \ J = max(\bigtriangleup + s_c - s, 0) minimize J=max(△+sc−s,0)
如果这里的margin △ \bigtriangleup △ 设为1,我们可以与支持向量机SVMs有很大的联系,最后的目标函数写成:
m i n i m i z e J = m a x ( 1 + U T f ( W x c + b ) − U T f ( W x + b ) , 0 ) minimize J = max(1 + U^Tf(Wx_c + b) - U^Tf(Wx+b), 0) minimizeJ=max(1+UTf(Wxc+b)−UTf(Wx+b),0)
1.5 反向传播训练
如果上面的目标函数为 0,因为这样不能计算梯度来进行SGD更新,那么就没必要去进行优化了。
反向传播是一种可以使用链式法则来计算模型前馈计算中使用的任何参数的损失梯度。从而利用 θ ( t + 1 ) = θ ( t ) − α ▽ θ ( t ) J \theta^{(t+1)} = \theta^{(t)} - \alpha \bigtriangledown_{\theta^{(t)}}J θ(t+1)=θ(t)−α▽θ(t)J 来进行参数的更新,利用下图来进行举例:

我们先统一一下符号:
- x i x_i xi为神经网络输入。
- s s s 为神经网络的输出。
- 每一层都有许多神经元来接收一个输入并产生一个输出,第 k k k 层的第 j j j 个神经元 接收的标量输入记为 z j ( k ) z_j^{(k)} zj(k),产生的标量激活输出为 a j ( k ) a_j^{(k)} aj(k)。
- 然后将 z j ( k ) z_j^{(k)} zj(k) 的反向传播误差记为 δ j ( k ) \delta_j^{(k)} δj(k)(这个在后面的error sharing中是关键部分)。
- 第一次没有激活函数,所以 x j = z j ( 1 ) = a j ( 1 ) x_j = z_j^{(1)} = a_j^{(1)} xj=zj(1)=aj(1)。
- W ( k ) W^{(k)} W(k)将第 k k k层的输出映射到 ( k + 1 ) (k + 1) (k+1)层的输入的传递矩阵。
我们假定损失函数 J = ( 1 + s c − s ) J = (1 + s_c - s) J=(1+sc−s) 为正,并且我们希望更新参数 W 14 ( 1 ) W_{14}^{(1)} W14(1)(如下图所示)。
我们知道 W 14 ( 1 ) W_{14}^{(1)} W14(1)只对 z 1 ( 2 ) z_1^{(2)} z1(2)产生贡献,而反向传播的梯度只受它们贡献的值的影响。接下来 a 1 ( 2 ) a_1^{(2)} a1(2)与 W 1 ( 2 ) W_1^{(2)} W1(2)相连接。
J = ( 1 + s c − s ) J = (1 + s_c - s) J=(1+sc−s) ,所以 ∂ J ∂ s = − ∂ J ∂ s c = − 1 \frac{\partial J}{\partial s} = - \frac{\partial J}{\partial s_c} = -1 ∂s∂J=−∂sc∂J=−1,
那么 ∂ s ∂ W i j ( 1 ) \frac{\partial s}{\partial W_{ij}^{(1)}} ∂Wij(1)∂s 推导如下(建议手推一遍):

则 ∂ s ∂ W i j ( 1 ) = δ i ( 2 ) ⋅ a j ( 1 ) \frac{\partial s}{\partial W_{ij}^{(1)}} = \delta_i^{(2)} \cdot a_j^{(1)} ∂Wij(1)∂s=δi(2)⋅aj(1)
在反向传播中有一个概念叫做"error sharing / distribution",也就是上面提到的 δ \delta δ 这一项。
我们用个简单的例子来阐述一下这个概念。
∂ s ∂ W = ∂ s ∂ h ∂ h ∂ z ∂ z ∂ W \frac{\partial s}{\partial W} = \frac{\partial s}{\partial h}\frac{\partial h}{\partial z}\frac{\partial z}{\partial W} ∂W∂s=∂h∂s∂z∂h∂W∂z 而 ∂ s ∂ b = ∂ s ∂ h ∂ h ∂ z ∂ z ∂ b \frac{\partial s}{\partial b} = \frac{\partial s}{\partial h}\frac{\partial h}{\partial z}\frac{\partial z}{\partial b} ∂b∂s=∂h∂s∂z∂h∂b∂z
我们可以发现前面 ∂ s ∂ h ∂ h ∂ z \frac{\partial s}{\partial h}\frac{\partial h}{\partial z} ∂h∂s∂z∂h 是共有的,所以令其为 δ \delta δ。


