二进制及其运算学习(原码、反码、补码、位运算)
学习背景:最近在看很多JAVA类的源码,遇到了很多的位运算,所以系统的学习了下有关二进制的知识。
首先,看一下JAVA中的基本数据的字节(Byte)长度和bit长度:
| 基本数据类型 | 字节Byte | bit |
|---|---|---|
| byte | 1字节 | 8位 |
| short | 2字节 | 16位 |
| int | 4字节 | 32位 |
| long | 8字节 | 64位 |
| float | 4字节 | 32位 |
| double | 8字节 | 64位 |
| boolean | 1字节(也说4字节) | 8位 |
| char | 2字节 | 16位 |
java是怎么记录数据的
计算机以二进制(0和1)来记录数据。在JAVA中根据基本数据类型的长度,高位没有记录数则,高位补0。首位记录数字的正负(0:正数;1:负数)。
比如 :
(int)15 : 0000,0000,0000,0000,0000,0000,0000,1111
(int)-15 :1000,0000,0000,0000,0000,0000,0000,1111 (原码)
(long)15: 0000,0000,0000,0000,0000,0000,0000,0000,0000,0000,0000,0000,0000,0000,0000,1111
原码、反码、补码
首先了解一下计算机的计算原理:在我们平常学的数学中,有+ 、- 、* 、/ 。而加减乘除在计算机中都可以用加法来记算,这样的计算机的计算逻辑简单,达到高效的效果。
减法可以使用加法运算,比如15-7可以使用15+(-7)来计算。
乘法是加法的累积,乘法在计算机运算中分为原码乘法和补码乘法,都是通过加法+位移的方式的运算。
除法是减法的累积,除法在计算机运算中也分为原码除法和补码除法,也都是通过加法+位移的方式的运算。
原码:用符号位和数值表示带符号数,正数的符号位用“0”表示,负数的符号位用“1”表示,数值部分用二进制形式表示。
举例:
| 十进制 | 二进制原码 |
|---|---|
| (int)7 | 0000,0000,0000,0000,0000,0000,0000,0111 |
| (int)-3 | 1000,0000,0000,0000,0000,0000,0000,0011 |
想一下,如果计算机只用原码来计算加法,则势必不能简单的把数字相加,一定需要考虑符号的情况,这样每次都得判断符号位的情况会使得计算的效率很低,所以引入了 反码 的概念,无需考虑符号位的情况,把符号位直接纳入到计算中,通过简单的加法完成。
反码:正数的反码与原码相同,负数的反码为对该数的原码除符号位外各位取反。
| 十进制 | 二进制原码 | 二进制反码 |
|---|---|---|
| (int)7 | 0000,0000,0000,0000,0000,0000,0000,0111 | 0000,0000,0000,0000,0000,0000,0000,0111 |
| (int)-3 | 1000,0000,0000,0000,0000,0000,0000,0011 | 1111,1111,1111,1111,1111,1111,1111,1100 |
我们现在再来通过加法来计算下 : 7+(-3)
| 计算过程 | 二进制 |
|---|---|
| (int)7 | 0000,0000,0000,0000,0000,0000,0000,0111 (反码) |
| (int)-3 | 1111,1111,1111,1111,1111,1111,1111,1100(反码) |
| 7+(-3) = | 0000,0000,0000,0000,0000,0000,0000,0011(反码) |
| 换算成原码 | 0000,0000,0000,0000,0000,0000,0000,0011(原码) |
| 换算成十进制 | 3 |
结果怎么不对呢?还差1,这个时候我们需要找下原因,看一下特殊的计算:
计算:1-1 等价于 1+(-1)
0000,0000,0000,0000,0000,0000,0000,0001(1的反码)
1111,1111,1111,1111,1111,1111,1111,1110(-1的反码)
1111,1111,1111,1111,1111,1111,1111,1111 (1+(-1)的反码)
1000,0000,0000,0000,0000,0000,0000,0000 (原码)
最后结果为: -0
计算:0+0
0000,0000,0000,0000,0000,0000,0000,0000(0的反码)
0000,0000,0000,0000,0000,0000,0000,0000(0的反码)
0000,0000,0000,0000,0000,0000,0000,0000 (0+0的反码)
1000,0000,0000,0000,0000,0000,0000,0000 (原码)
最后结果为: 0
由此可知:二进制使用符号位表示正负,在计算正数和负数相加的时候,由于符号位参与了计算,多了一个【-0】的位数,所以结果会差1;而在计算正数相加的时候,由于正数的反码和补码一样,符号位并不会实际影响最后的结果,也就是避开了-0这个位数。
那么怎么解决这个问题,由此引入了补码。
补码:正数的补码与原码相同,负数的补码为对该数的原码除符号位外各位取反,然后在最后一位加1
| 十进制 | 二进制原码 | 二进制反码 | 二进制补码 |
|---|---|---|---|
| (int)7 | 0000,0000,0000,0000,0000,0000,0000,0111 | 0000,0000,0000,0000,0000,0000,0000,0111 | 0000,0000,0000,0000,0000,0000,0000,0111 |
| (int)-3 | 1000,0000,0000,0000,0000,0000,0000,0011 | 1111,1111,1111,1111,1111,1111,1111,1100 | 1111,1111,1111,1111,1111,1111,1111,1101 |
现在,再来计算一下: 7+(-3)
| 计算过程 | 二进制 |
|---|---|
| (int)7 | 0000,0000,0000,0000,0000,0000,0000,0111 (补码) |
| (int)-3 | 1111,1111,1111,1111,1111,1111,1111,1101(补码) |
| 7+(-3) = | 0000,0000,0000,0000,0000,0000,0000,0100(补码) |
| 换算成原码 | 0000,0000,0000,0000,0000,0000,0000,0100(原码) |
| 换算成十进制 | 4 |
计算结果正确。
注意:原码与反码,互为反码;原码与补码,互为补码;
比如:
原码转为反码和反码转为原码
| 原码转反码(符号位不变,其余位取反) | 反码转原码(同样是符号位不变,其余位取反) |
|---|---|
| 1000,0000,0000,0000,0000,0000,0000,0011(原码) | 1111,1111,1111,1111,1111,1111,1111,1100(反码) |
| 1111,1111,1111,1111,1111,1111,1111,1100 (反码) | 1000,0000,0000,0000,0000,0000,0000,0011(原码) |
原码转为补码和补码转原码
| 原码转反码(符号位不变,其余位取反,再+1) | 反码转原码(同样是符号位不变,其余位取反,再+1) |
|---|---|
| 1000,0000,0000,0000,0000,0000,0000,0011(原码) | 1111,1111,1111,1111,1111,1111,1111,1101(补码) |
| 1111,1111,1111,1111,1111,1111,1111,1101 (补码) | 1000,0000,0000,0000,0000,0000,0000,0011(原码) |
二进制的位运算
再来学习一下,二进制的位运算
二进制中的1和0,我们也可以理解为真假,即1:真;0:假。
&: 与
计算规则:有0为0,同时为1才为1
辅助记忆:真真为真 真假为假 假假为假
| 十进制 | 二进制原码 |
|---|---|
| (int)7 | 0000,0000,0000,0000,0000,0000,0000,0111 |
| (int)3 | 0000,0000,0000,0000,0000,0000,0000,0011 |
| 7&3 = 3 | 0000,0000,0000,0000,0000,0000,0000,0011 |
|: 或
计算规则:有1为1,同时为0才为0
辅助记忆:真真为真 真假为真 假假为假
| 十进制 | 二进制原码 |
|---|---|
| (int)7 | 0000,0000,0000,0000,0000,0000,0000,0111 |
| (int)3 | 0000,0000,0000,0000,0000,0000,0000,0011 |
| 7|3 = 7 | 0000,0000,0000,0000,0000,0000,0000,0111 |
~: 非
计算规则:按位取反(包括符号位)
| 十进制 | 二进制 |
|---|---|
| (int)7 | 0000,0000,0000,0000,0000,0000,0000,0111 |
| ~7 = -8 | 1111,1111,1111,1111,1111,1111,1111,1000 |
^: 异或
计算规则:相同为0,不同为1
辅助记忆:真真为假 真假为真 假假为假
| 十进制 | 二进制原码 |
|---|---|
| (int)7 | 0000,0000,0000,0000,0000,0000,0000,0111 |
| (int)3 | 0000,0000,0000,0000,0000,0000,0000,0011 |
| 7^3 = 4 | 0000,0000,0000,0000,0000,0000,0000,0100 |
位移运算:使用补码位移
<<:有符号左移
规则:丢弃高位,低位补0
在数字没有溢出的前提下,对于正数和负数,左移n位就相当于乘以2的n次方。
注意“”如果移动的位数超过了该类型的最大位数,那么编译器会对移动的位数取模。如对int型移动33位,实际上只移动了33%32=1位
| 十进制 | 二进制原码 |
|---|---|
| (int)3 | 0000,0000,0000,0000,0000,0000,0000,0011(正数补码 = 原码) |
| 3<<2 = 12 | 0000,0000,0000,0000,0000,0000,0000,1100 (正数补码 = 原码) |
| 十进制 | 二进制原码 |
|---|---|
| (int)-3 | 1111,1111,1111,1111,1111,1111,1111,1101(补码) |
| -3<<2 = -12 | 1111,1111,1111,1111,1111,1111,1111,0100 (补码) |
| -12 | 1000,0000,0000,0000,0000,0000,0000,1100 (原码) |
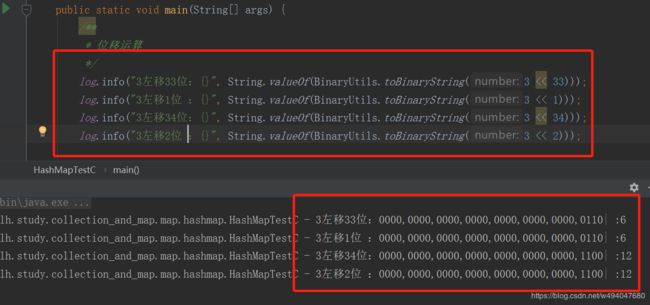
左移超过数据类型最大位,取模移位。
如图:
3 << 33 等价于:3 << 1
3 << 34 等价于:3 << 2
>>:有符号右移
规则:符号位不变,丢弃低位,高位补上符号位
正数右移n位相当于除以2的n次方(取整)。
负数右移n位相当于除以2的n次方(取整 + (-1))。
注意“”如果移动的位数超过了该类型的最大位数,那么编译器会对移动的位数取模。如对int型移动33位,实际上只移动了33%32=1位。
在未超出该数据类型的最大位数:全部移动出去的情况,整个高位使用0表示,那就是全都是0,结果自然为0;负数整个高位为1,那就是全都是1,结果自然为-1
| 十进制 | 二进制原码 |
|---|---|
| (int)7 | 0000,0000,0000,0000,0000,0000,0000,0111(正数补码 = 原码) |
| 7>>2 = 1 | 0000,0000,0000,0000,0000,0000,0000,0001 (正数补码 = 原码) |
| 十进制 | 二进制原码 |
|---|---|
| (int)-7 | 1111,1111,1111,1111,1111,1111,1111,1001(补码) |
| -7>>2 = -2 | 1111,1111,1111,1111,1111,1111,1111,1110 (补码) |
| -2 | 1000,0000,0000,0000,0000,0000,0000,0010 (原码) |
>>>: 无符号右移
规则:不论正负,高位均补0
注意“”如果移动的位数超过了该类型的最大位数,那么编译器会对移动的位数取模。如对int型移动33位,实际上只移动了33%32=1位。
| 十进制 | 二进制原码 |
|---|---|
| (int)7 | 0000,0000,0000,0000,0000,0000,0000,0111(正数补码 = 原码) |
| 7>>>2 = 1 | 0000,0000,0000,0000,0000,0000,0000,0001 (正数补码 = 原码) |
| 十进制 | 二进制原码 |
|---|---|
| (int)-7 | 1111,1111,1111,1111,1111,1111,1111,1001(补码) |
| -7>>>2 = 1073741822 | 0011,1111,1111,1111,1111,1111,1111,1110 (补码 ) |
| 1073741822 | 0011,1111,1111,1111,1111,1111,1111,1110 (原码) |
<<<: 无符号左移 :没有无符号左移
先写到这里。。。以后有具体的应用再补充了。。。

