TreeMap源码分析(红黑树的实现过程)
一、前言
TreeMap的实现本质上就是红黑树的实现,本文将通过TreeMap源码探究红黑树的实现过程。
PS:题外话,推荐一个制作矢量图的工具:DIA 支持中文
二、红黑树
1、二叉查找树概念
在看红黑树之前,我们先了解一下 二叉查找树(Binary Search Tree)
二叉查找树具有以下特点:
1.左子树上所有结点的值均小于或等于它的根结点的值。
2.右子树上所有结点的值均大于或等于它的根结点的值。
3.左、右子树也分别为二叉排序树
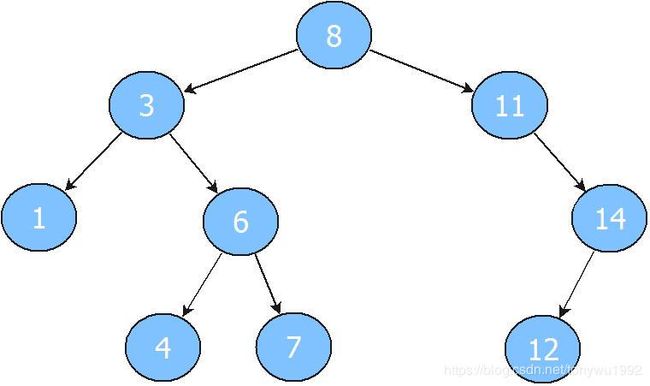
上面是一颗平衡二叉树,时间复杂度为O(logN),但普通的二叉查找树是存在很大缺陷的,很容易在插入的过程中失衡,变成一颗左树/右树,如下图所示:

这种二叉树大大降低了查找效率,时间复杂度变升高为O(N)。为了维持二叉树的平衡,这里引入了红黑树的概念
2、红黑树概念
红黑树(Red Black Tree) 在二叉树的基础上还具有以下的限制:
①节点是红色或黑色。
②根节点是黑色。
③每个叶子节点都是黑色的空节点(NIL节点)。
④每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
⑤从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
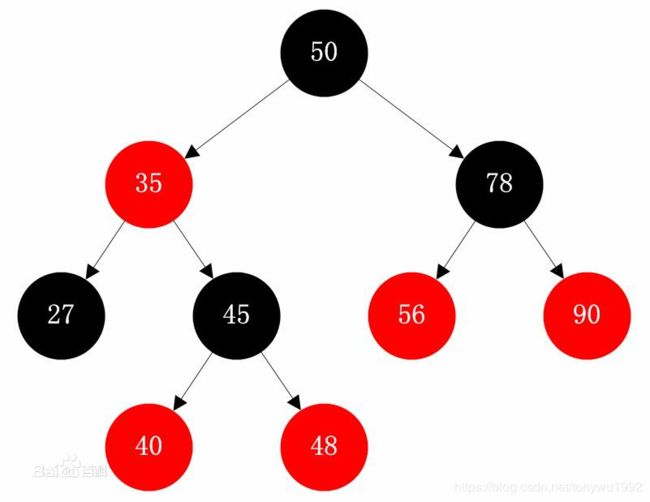
上图就是一颗红黑树,满足红黑树的5点要求。正是因为这5点限制条件,才保证了红黑树的平衡。红黑树从根到叶子的最长路径不会超过最短路径的2倍。
当插入、删除节点的时候,红黑树的规则有可能被打破,为了防止规则被打破调整的方法有两种:变色和旋转,其中旋转包括左旋转和右旋转。
左旋转: 将X的右孩子Y绕X逆时针旋转,使得X被Y替代,而X的右孩子Y成为X的父亲,自己成为Y的左孩子,同时还需要修改相关节点的引用。
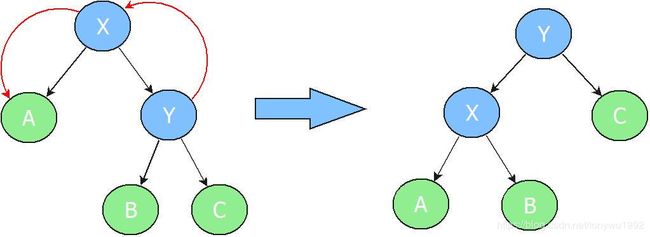
右旋转: 将X的左孩子Y绕X顺时针旋转,使得X被Y替代,而X的左孩子Y成为X的父亲,自己成为Y的右孩子,同时还需要修改相关节点的引用。
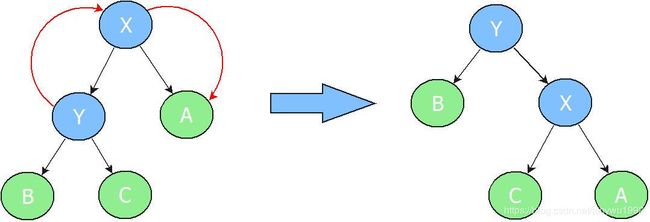
刚接触可能不是很清楚,从博客上找了一张GIF方便大家理解,也后面可以根据代码一步步理解旋转的过程

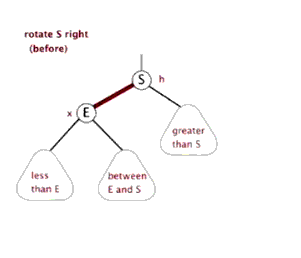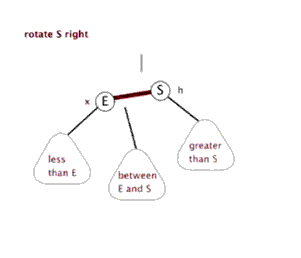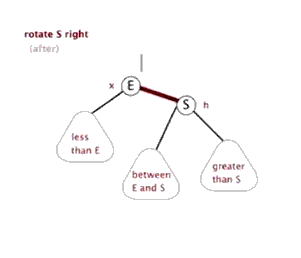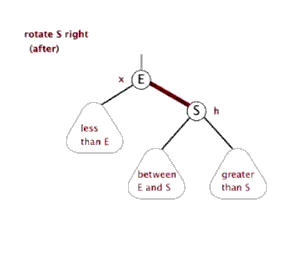
动图来源:https://www.cnblogs.com/yangecnu/p/Introduce-Red-Black-Tree.html
红黑树的基础概念就介绍到这里,下面一起探究下TreeMap对于红黑树的具体实现
三、TreeMap
1、TreeMap数据结构
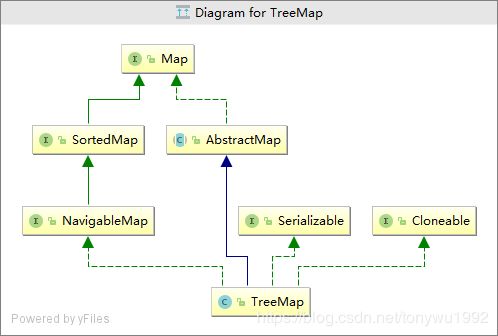
public class TreeMap<K,V>
extends AbstractMap<K,V>
implements NavigableMap<K,V>, Cloneable, java.io.Serializable
AbstractMap:TreeMap是一个key-value集合
NavigableMap:TreeMap支持扩展的导航方法
Cloneable:TreeMap可以被克隆
Serializable:TreeMap支持序列化
TreeMap的几个重要属性:
/**
* 用于维护treemap顺序的比较器,如果为null则采用key元素的自然排序
*/
private final Comparator<? super K> comparator;
/**
* 根节点
*/
private transient Entry<K,V> root;
/**
* 节点数量
*/
private transient int size = 0;
/**
* 修改次数
*/
private transient int modCount = 0;
root是该红黑树的根节点。类型为Entry,后面会详细介绍
comparator比较器,红黑树在排序时,Entry中的key先通过指定的比较器进行排序,没有指定的话用元素默认的比较器进行排序(要求key必须实现Comparable接口)
下面看一下TreeMap的核心:内部类Entry-节点
static final class Entry<K,V> implements Map.Entry<K,V> {
//键
K key;
//值
V value;
//左孩子节点
Entry<K,V> left;
//右孩子节点
Entry<K,V> right;
//父节点
Entry<K,V> parent;
//该节点颜色,默认黑色
boolean color = BLACK;
/**
* 通过key、value、父节点构建一个Entry,默认黑色
*/
Entry(K key, V value, Entry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
public K getKey() {
return key;
}
public V getValue() {
return value;
}
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
public int hashCode() {
int keyHash = (key==null ? 0 : key.hashCode());
int valueHash = (value==null ? 0 : value.hashCode());
return keyHash ^ valueHash;
}
public String toString() {
return key + "=" + value;
}
}
2、TreeMap put()方法
红黑树新增节点
- 首先找到插入节点的位置。这里处理很简单,将红黑树当做一颗二叉查找树从顶端开始进行比较查找就行了
- 新插入的节点设为红色。为什么要设为红色呢,这是因为设为红色不会违反红黑树第五条限制,即:从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
- 若新插入节点的父节点为黑色,不会违反任何限制
- 若新插入节点的父节点为红色,则违反了第四条限制,即:每个红色节点的两个子节点都是黑色。这时候就需要通过变色和旋转调整红黑树已满足限制要求
下面我们就来看下新增节点会有哪几种情况以及我们如何相应的处理:
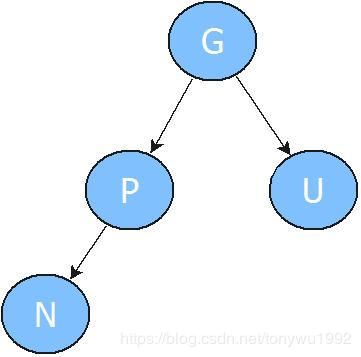
首先我们确定一个新增的基础模型:N为新增节点(New),P为它的父节点(Parent),U为它的叔父节点(Uncle),G为它的祖父节点(GrandPa)。这个模型将适用于③④⑤情况。
注意:后面讨论的情况是新增节点N的父节点P为G的左孩子,若是右孩子则互换左旋/右旋即可,就不再举例细说了
①为根节点
最简单的情况,直接插入,设置为根节点,颜色为默认的黑色
②父节点为黑色
直接插入,颜色设为红色。这样也不会违背红黑树的限制条件
③父节点P为红色,叔父节点U也为红色
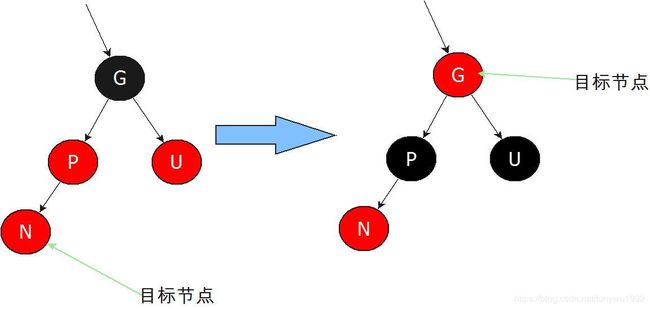
这种情况直接插入后N、P都为红色节点,违反了第4条限制,红黑树需要做出调整:P、U节点变为黑色,G节点变为红色。就这一块节点看来是满足了红黑树限制,但是还存在2种情况会打破限制:
- G节点为根节点,违反了第2条限制,这个简单,直接将G变为黑色就可以了
- G节点的父节点为红色,又违反了第四条限制,这时候我们将目标节点从N指向G,递归处理
④父节点P为红色,叔父节点U为黑色或NIL,且N为P的右孩子
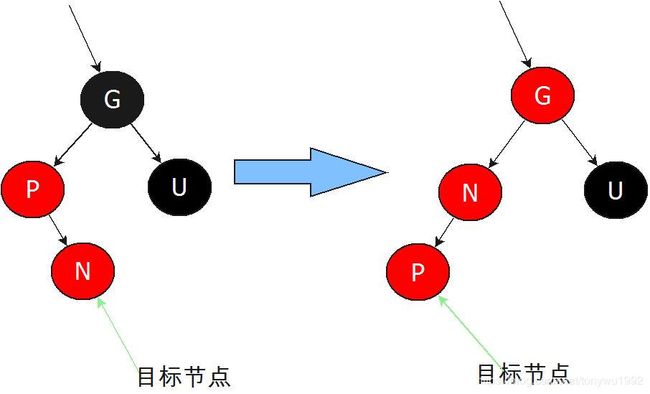
先将操作节点指向N的父节点P,再左旋P节点,这样就将其转换成了第⑤种情况
⑤父节点P为红色,叔父节点U为黑色或NIL,且N为P的左孩子

先将N的父节点P颜色变为黑色,N的祖父节点G颜色变为红色,再对G节点做右旋转,此时红黑树达到平衡。
特别注意
如果只看上面的图你可能会想:不对啊,这个时候右边的树明明多了一个黑色节点,怎么就平衡了呢?
这是因为:1:U节点可能是NIL节点 2:N节点可能是之前递归后的节点,N是一个整体,里面包含了黑色节点 3:N节点是可能有兄弟节点的 不要只局限于图里能看到的节点哦
put()代码实现
public V put(K key, V value) {
//用t表示当前操作的节点,从root根节点开始
Entry<K,V> t = root;
//如果根节点不存在,说明是一颗空树,直接创建根节点--->情况1
if (t == null) {
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
//用于记录比较的结果
int cmp;
//父节点
Entry<K,V> parent;
// split comparator and comparable paths
//指定的排序比较器
Comparator<? super K> cpr = comparator;
//如果有指定的比较器,则用它维护TreeMap元素顺序
if (cpr != null) {
do {
//parent指向上次循环的节点t
parent = t;
//比较新增节点的key和当前节点t的key值大小
cmp = cpr.compare(key, t.key);
//如果新插入的节点较小,则以当前节点的左孩子作为新的当前节点
if (cmp < 0)
t = t.left;
//如果新插入的节点较大,则以当前节点的右孩子作为新的当前节点
else if (cmp > 0)
t = t.right;
//如果新插入的节点和当前节点key值一样,则直接覆盖值并返回
else
return t.setValue(value);
//t=null时停止循环,说明此时已经没有需要比较的节点了,意味着已经找到了插入位置
} while (t != null);
}
//没有指定的比较器,用元素自身的自然顺序排序
else {
//key值不能为null,且必须实现Comparable接口
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
//处理过程同上
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//根据找到的父节点创建新的节点
Entry<K,V> e = new Entry<>(key, value, parent);
//若新节点key值小于父节点key值,则插入在父节点左侧
if (cmp < 0)
parent.left = e;
//若新节点key值大于父节点key值,则插入在父节点右侧
else
parent.right = e;
//插入后可能破坏红黑树的限制条件,需要做调整
fixAfterInsertion(e);
//TreeMap元素个数+1
size++;
//修改次数+1
modCount++;
return null;
}
/**
* 新增节点后红黑树的调整
*/
private void fixAfterInsertion(Entry<K,V> x) {
//插入节点设为红色
x.color = RED;
//若节点x为根节点或者父节点为红色则停止循环,调整结束。其他场景需要继续调整 --->包含了情况2
while (x != null && x != root && x.parent.color == RED) {
//如果x节点的父节点是祖父节点的左孩子
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
//获取x的叔父节点y
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
//若叔父节点y为红色---->情况3
if (colorOf(y) == RED) {
//将x节点的父节点设为黑色
setColor(parentOf(x), BLACK);
//将x的叔父节点y设为黑色
setColor(y, BLACK);
//将x的祖父节点设为红色
setColor(parentOf(parentOf(x)), RED);
//将x重新指向祖父节点,若其父节点为红色则继续循环做调整
x = parentOf(parentOf(x));
//若叔父节点y为黑色或NIL(情况4、情况5)
} else {
//若x为父节点的右孩子(情况4)
if (x == rightOf(parentOf(x))) {
//将x重新指向父节点并做左旋转,这将会调整为情况5
x = parentOf(x);
rotateLeft(x);
}
//若x为父节点的左孩子(情况5)
//将x父节点设为黑色
setColor(parentOf(x), BLACK);
//将x祖父节点设为红色
setColor(parentOf(parentOf(x)), RED);
//对x祖父节点做右旋转
rotateRight(parentOf(parentOf(x)));
}
//如果x节点的父节点是祖父节点的右孩子,调整方法类似,只是区分左/右旋
} else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
左旋/右旋操作,只看代码和注释很难理解,强烈建议结合上面的静态图/动态图自己动手画画,这将让你更好的理解左/右旋的过程
/**
* 左旋
*/
private void rotateLeft(Entry<K,V> p) {
//p为左旋的操作节点
if (p != null) {
//获取p的右孩子r
Entry<K,V> r = p.right;
//将r的左孩子设为p的右孩子
p.right = r.left;
//若r的左孩子不是NIL节点则将p设为r左孩子的父节点
if (r.left != null)
r.left.parent = p;
//将p的父节点设为r的父节点
r.parent = p.parent;
//若p的父节点是NIL,则说明之前的P节点为root节点,那么现在将r设为root节点
if (p.parent == null)
root = r;
//若p是父节点的左孩子,则将r设为p的父节点的左孩子,否则设置为右孩子
else if (p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
//最后将p设为r的左孩子,r设为p的父节点
r.left = p;
p.parent = r;
}
}
/**
*右旋
*/
private void rotateRight(Entry<K,V> p) {
//p为左旋的操作节点
if (p != null) {
//获取p的左孩子l
Entry<K,V> l = p.left;
//将l的右孩子设为p的左孩子
p.left = l.right;
//若l的右孩子不是NIL节点则将p设为l右孩子的父节点
if (l.right != null) l.right.parent = p;
//将p的父节点设为l的父节点
l.parent = p.parent;
//若p的父节点是NIL,则说明之前的P节点为root节点,那么现在将l设为root节点
if (p.parent == null)
root = l;
//若p是父节点的右孩子,则将l设为p的父节点的右孩子,否则设置为左孩子
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
//最后将p设为l的右孩子,l设为p的父节点
l.right = p;
p.parent = l;
}
}
3、TreeMap remove()方法
在讨论红黑树删除节点前,我们先看一下普通的二叉查找树应该如何删除节点
二叉查找树删除节点
- 若删除节点不存在任何一个孩子,直接删除即可
- 若删除节点有且仅有一个孩子,用孩子顶替删除节点并删除
- 若删除节点有两个孩子,我们可以寻找后继节点,之后将后继节点的值复制给删除节点,那么接下来只需要删除后继节点即可,这样就转化为了前2种情况(后继节点最多存在1个孩子)
前2种情况很容易理解,我们详细看一下第3种情况:
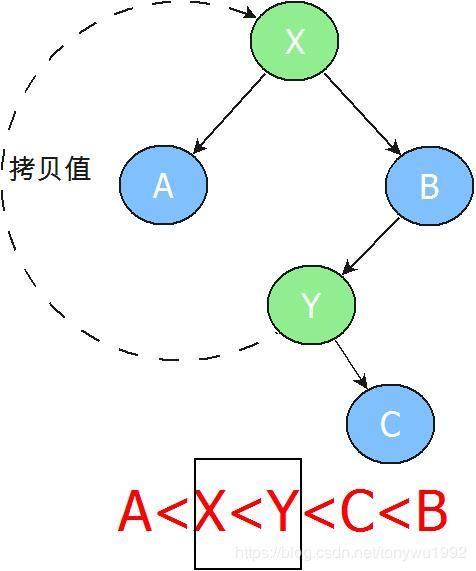
寻找后继节点,即寻找该节点右子树最小的节点,也就是该节点右子树最左边的那个节点。如下图所示,若将树的所有元素压平,其实就是找比X大的节点中最小的那个Y。
之后将Y的值赋给X,接下来考虑的就是如何删除Y节点了,此时Y节点只有2种情况:1、没有子节点 2、只有一个右孩子(如果Y有左孩子,那么X的后继节点就不是Y了呀!而是Y的左孩子)。那么我们就成功的将其转化为了前2种情况继续处理
PS:除了后继节点还有前驱节点,如Y的前驱节点就是X,也就是向上查找,找到比Y小的节点中最大的那个。TreeMap删除流程中不用考虑这种情况,这个从后面源码中就可以看出
以上就是在普通的二叉查找树中删除的处理过程,那么在红黑树中需要做什么额外的处理呢?
红黑树删除节点
经过上面的操作,我们实际上只需要考虑 待删除节点有一个孩子 的情况(若没有孩子,我们将任意一个NIL黑色节点当做它的孩子)
若删除的节点是红色,直接删除,并不会违反红黑树的任何限制条件。(第4、5两条限制)
若删除的节点是黑色,那么所有经过该节点路径上的黑色节点数量就少了一个,则会违反红黑树的第五条限制,即:从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。这时候还要分2种情况:
- 若待删除节点孩子节点为红色,那么直接用孩子节点顶替待删除节点,再将孩子节点设为黑色,就满足了第5条限制
- 若孩子节点也为黑色(别忘了NIL也是黑色的哦),这种情况下由于删除节点是黑色,且只有一个黑色孩子节点,另一个是NIL,那么此时这个孩子节点必定是NIL,否则违反限制5。也就是说此时待删除节点为黑色,两个孩子理论都是NIL节点。
这种情况比较复杂,下面的所有可能性讨论的都是这种情况。
请务必耐心阅读以下内容,这会让你更好的理解最终删除节点和它的孩子均为黑色的这种情况(wiki中文版关于这段描述没有英文的到位,故选用英文描述)。包括之后6种情况有兴趣的也可以看下英文wiki的解释,中文有部分内容像是机翻~
维基百科------红黑树中关于最终删除节点和它的孩子均为黑色的具体说明(中文版)
维基百科------红黑树中关于最终删除节点和它的孩子均为黑色的具体说明(英文版)
The complex case is when both M(最终待删除节点) and C(它的孩子) are black. (This can only occur when deleting a black node which has two leaf children, because if the black node M had a black non-leaf child on one side but just a leaf child on the other side, then the count of black nodes on both sides would be different, thus the tree would have been an invalid red–black tree by violation of property 5.) We begin by replacing M with its child C – we recall that in this case “its child C” is either child of M, both being leaves. We will relabel this child C (in its new position) N(N指向C), and its sibling (its new parent’s other child) S. (S was previously the sibling of M.) In the diagrams below, we will also use P for N’s new parent (M’s old parent), SL for S’s left child, and SR for S’s right child (S cannot be a leaf because if M and C were black, then P’s one subtree which included M counted two black-height and thus P’s other subtree which includes S must also count two black-height, which cannot be the case if S is a leaf node).
Note: In order for the tree to remain well-defined, we need every null leaf to remain a leaf after all transformations (that it will not have any children). If the node we are deleting has a non-leaf (non-null) child N, it is easy to see that the property is satisfied. If, on the other hand, N would be a null leaf, it can be verified from the diagrams (or code) for all the cases that the property is satisfied as well.
We can perform the steps outlined above with the following code, where the function replace_node substitutes child into n’s place in the tree. For convenience, code in this section will assume that null leaves are represented by actual node objects rather than NULL (the code in the Insertion section works with either representation).
void replace_node(struct node* n, struct node* child){
child->parent = n->parent;
if (n == n->parent->left)
n->parent->left = child;
else
n->parent->right = child;
}
void delete_one_child(struct node* n)
{
/*
* Precondition: n has at most one non-leaf child.
*/
struct node* child = is_leaf(n->right) ? n->left : n->right;
replace_node(n, child);
if (n->color == BLACK) {
if (child->color == RED)
child->color = BLACK;
else
delete_case1(child);
}
free(n);
}
Note: If N is a null leaf and we do not want to represent null leaves as actual node objects, we can modify the algorithm by first calling delete_case1() on its parent (the node that we delete, n in the code above) and deleting it afterwards. We do this if the parent is black (red is trivial), so it behaves in the same way as a null leaf (and is sometimes called a ‘phantom’ leaf). And we can safely delete it at the end as n will remain a leaf after all operations, as shown above. In addition, the sibling tests in cases 2 and 3 require updating as it is no longer true that the sibling will have children represented as objects.
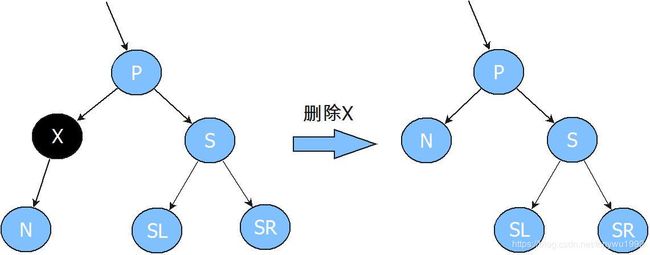
首先我们确定一个删除调整的基础模型,X为最终待删除节点,N为它的孩子,P为它的父节点,B为它的兄弟节点,BL为B的左孩子,BR为B的右孩子。
重要!!!几乎没有文章提到这个问题
这里很容易让人引起误解,因为我们说过这种情况下X是黑色,X最多只有一个孩子节点,并且N也是黑色,那么很明显N其实是一个NIL叶子节点,否则就违反了红黑树的限制5。那么这个模型可能让很多人感到困惑,因为此时N实际上是一个NIL节点,莫非我们之后都是操作一个空节点?为了出于方便,我们并不想用NULL去代表一个实际节点对象,所以我们修改作用对象,改为操作它原来的父节点(也就是真正被删除的节点X),它的行为等同于操作NULL节点(因为X会被删除,有时也称它为“幻影”叶子节点),最后我们可以安全的删除它因为在所有操作过后仍然是一个叶子节点。
这里不是太好理解,有点抽象,请结合英文wiki阅读
注意:后面讨论的情况是N为父节点P的左孩子,若是右孩子则互换左旋/右旋即可,就不再举例细说了
①N为新的根节点
在这种情况下,就结束了。我们从所有路径上移除了一个黑色节点,并且新的根是黑色的,没有违反任何限制
这是wiki上的描述,我觉得它指的就是删除根节点,并且孩子均为NIL节点,此时用NIL节点替代根节点
②N为黑色,兄弟节点S为红色
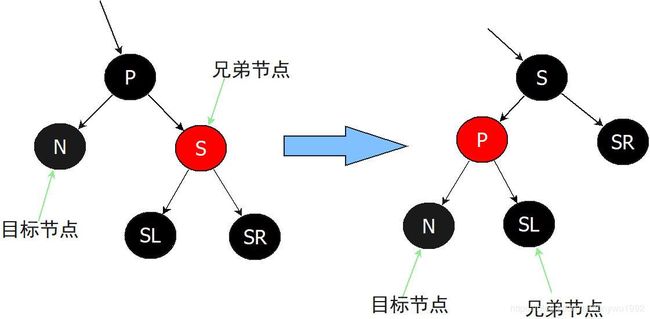
因为兄弟节点S为红色,所以SL、SR、P肯定是黑色。此时将S设为黑色,P设为红色,左旋P节点,最后再将兄弟节点指向SL,此时我们就将其转换为了④⑤⑥情况
注意:我们的模型是删除了黑色节点X,N是接替它的位置。所以整个过程由P->X->N变为P->N,比未经过N节点的路径少了一个黑色节点,违反了红黑树第5条限制,所以还需要调整
③N为黑色,P、S、SL、SR也均为黑色
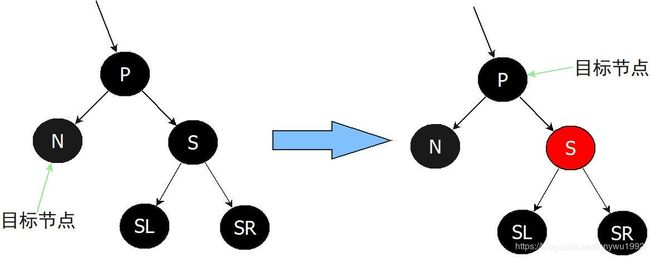
这种情况下,直接把S设为红色。这样通过S的所有路径都比之前少了一个黑色节点,而之前删除了N的初始父亲X导致通过N的所有路径也少了一个黑色节点,这样经过N的路径和经过S的路径黑色节点数量就一样了。但是所有经过P的路径比不经过P的路径少了一个黑色节点,违反了红黑树第5条限制,所以这时候我们需要将目标节点设为P,重新进行处理
④N为黑色,P为红色,S、SL、SR均为黑色

交换P、S颜色,这样并不会影响通过S的路径黑色节点数量,但这样在通过N的路径上新增了一个黑色节点,弥补了之前被删掉的黑色X
⑤N为黑色,S为黑色,SL为红色,SR为黑色

此时P的颜色可红可黑,将SL颜色设为黑色,S颜色设为红色,对S节点做右旋转,N的兄弟节点重新指向SL,且SL的右孩子为红色,我们就将其转化为了第⑥种情况
⑥N为黑色,S为黑色,SR为红色

此时P和SL的颜色可红可黑,将S的颜色设为P的颜色,P的颜色设为黑色,SR的颜色设为黑色,对P做左旋转。
此时N会多出一个额外的黑色祖先:1、P变为了黑色 2、P原本就是黑色的,那么S就会作为一个新增的黑色祖父节点。因此通过N的路径会多出1个黑色节点,这样就弥补了之前删除的黑色X
对于不经过N的路径有2种可能性:
1、它通过N的新兄弟节点SL,那么它之前一定是经过了S和P。而在转换后S和P只是交换了颜色和位置,因此该路径包含了相同数量的黑色节点
2、它通过N的新叔父节点SR,那么它之前一定经过了P、S、SR(红色),但是现在只经过了S、SR,少了一个黑色节点,会违反红黑树第5条限制。并且由于S节点可红可黑,若S节点是红色的,SR也是红色的话就违反了红黑树第4条限制。此时只需要将SR由红色设为黑色,就满足了所有要求
remove()代码实现
public V remove(Object key) {
//根据key查找对应的节点
Entry<K,V> p = getEntry(key);
if (p == null)
return null;
//记录对应的value用于返回
V oldValue = p.value;
//删除节点
deleteEntry(p);
return oldValue;
}
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
// If strictly internal, copy successor's element to p and then make p
// point to successor.
//若待删除节点的左右孩子均存在,则需要寻找它的后继节点
if (p.left != null && p.right != null) {
//查找p节点的后继节点s,并将后继节点s的值复制到原本删除节点p上,最后将p指向s
//这样就完成了复制值操作,并且将其转化为了删除后继节点(最多只有1个孩子)
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// Start fixup at replacement node, if it exists.
//p是待删除节点,就是上文所说的X
//replacement是p的替代节点,就是上文所说的N
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
//若替代节点不是NIL节点
if (replacement != null) {
// Link replacement to parent
//将p的父节点设为replacement的父节点
replacement.parent = p.parent;
//若p的父节点为空,则将replacement设为root节点
if (p.parent == null)
root = replacement;
//若p为其父节点的左孩子,则将replacement设为p父节点的左孩子
else if (p == p.parent.left)
p.parent.left = replacement;
//若p为其父节点的右孩子,则将replacement设为p父节点的右孩子
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
//将p节点左右孩子、父节点均设为空,等待gc回收,相当于删除了p节点
p.left = p.right = p.parent = null;
// Fix replacement
//若p节点为黑色则需要调整红黑树已满足所有条件
if (p.color == BLACK)
fixAfterDeletion(replacement);
//若替代节点为空,且p的父节点为空,说明p为root节点,直接删除
} else if (p.parent == null) { // return if we are the only node.
root = null;
//若替代节点为空
} else { // No children. Use self as phantom replacement and unlink.
//注意上面的注释Use self as phantom replacement
//这也就是我们上文所提到的“幻影节点”:为了出于方便,我们并不想用NULL去代表一个实际节点对象,所以我们修改作用对象,
//改为操作它原来的父节点(也就是真正被删除的节点X),它的行为等同于操作NULL节点(因为X会被删除,有时也称它为“幻影”叶子节点)
//若p节点为黑色则需要调整红黑树已满足所有条件
if (p.color == BLACK)
fixAfterDeletion(p);
//解除p的所有引用,等待gc回收
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
//寻找后继/前驱节点,也就是右子树的最左孩子或者左子树最右孩子
static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if (t == null)
return null;
else if (t.right != null) {
Entry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else {
Entry<K,V> p = t.parent;
Entry<K,V> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
//注意这里和上文中的关系 x=N sib=S
private void fixAfterDeletion(Entry<K,V> x) {
//当x指向为根节点或者红色时停止调整
while (x != root && colorOf(x) == BLACK) {
//若x是父节点的左孩子
if (x == leftOf(parentOf(x))) {
//x的兄弟节点sib
Entry<K,V> sib = rightOf(parentOf(x));
//若兄弟节点sib是红色
if (colorOf(sib) == RED) {
//将兄弟节点sib设为黑色
setColor(sib, BLACK);
//将x的父节点设为红色
setColor(parentOf(x), RED);
//对x的父节点做左旋转
rotateLeft(parentOf(x));
//将sib指向旋转后的兄弟节点
sib = rightOf(parentOf(x));
}
//若兄弟节点sib的两个孩子都是黑色
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
//将兄弟节点sib设为红色
setColor(sib, RED);
//x指向x的父亲继续调整
x = parentOf(x);
} else {
//若兄弟节点sib的右孩子是黑色,左孩子是红色
if (colorOf(rightOf(sib)) == BLACK) {
//将兄弟节点sib的左孩子设为黑色
setColor(leftOf(sib), BLACK);
//将兄弟节点sib设为红色
setColor(sib, RED);
//对兄弟节点sib做右旋转
rotateRight(sib);
//将sib指向旋转后的兄弟节点
sib = rightOf(parentOf(x));
}
//若兄弟节点sib的右孩子是红色
//将兄弟节点sib设为x父节点的颜色
setColor(sib, colorOf(parentOf(x)));
//将x父节点设为黑色
setColor(parentOf(x), BLACK);
//将兄弟节点sib的右孩子设为黑色
setColor(rightOf(sib), BLACK);
//对x父节点做左旋转
rotateLeft(parentOf(x));
//x指向root,结束调整
x = root;
}
//若x是父节点的右孩子,镜像操作
} else { // symmetric
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
五、结语
TreeMap源码分析就结束了,主要看了put()以及remove()方法,同时深入探究了红黑树的结构以及新增/删除节点的各种情况。尤其是删除节点,调整过程较为复杂,特别是在待删除节点X以及替代节点N都为黑色这种情况下更是分为多种子情况,希望大家能静下心来理解那个基础模型,看一下英文wiki对于它的解释。
参考文档
Java集合干货系列-(四)TreeMap源码解析
WIKI:Red–black tree
WIKI:红黑树