1. 标题:分机号
X老板脾气古怪,他们公司的电话分机号都是3位数,老板规定,所有号码必须是降序排列,且不能有重复的数位。比如:
751,520,321 都满足要求,而,
766,918,201 就不符合要求。
现在请你计算一下,按照这样的规定,一共有多少个可用的3位分机号码?
请直接提交该数字,不要填写任何多余的内容。
这题用代码和逻辑都比较简单.
public class _1 {
public static void main(String[] args) {
int counter = 0;
for(int i = 1; i <= 9; i++){
for(int j = 0; j <= 9; j++){
for(int m = 0; m <= 9; m++){
if(i > j && j > m){
counter ++;
}
}
}
}
}
System.out.println(counter);
}
}//结果: 120
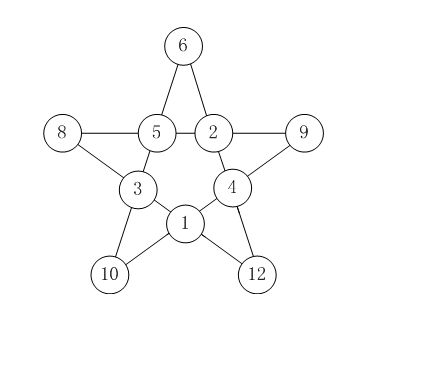
标题:五星填数
如【图1.png】的五星图案节点填上数字:1~12,除去7和11。
要求每条直线上数字和相等。
如图就是恰当的填法。
请你利用计算机搜索所有可能的填法有多少种。
注意:旋转或镜像后相同的算同一种填法。
请提交表示方案数目的整数,不要填写任何其它内容。
package sort;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
int count = 0;
int counter = 0;
int[] a = new int[12];
// 先写出所有 1-12 的全排列.
for (a[0] = 1; a[0] <= a.length; a[0]++) {
if (a[0] == 7 || a[0] == 11) {
continue;
}
for (a[1] = 1; a[1] <= a.length; a[1]++) {
if (isRepeat(a, 1)) {
continue;
}
if (a[1] == 7 || a[1] == 11) {
continue;
}
for (a[2] = 1; a[2] <= a.length; a[2]++) {
if (isRepeat(a, 2)) {
continue;
}
if (a[2] == 7 || a[2] == 11) {
continue;
}
for (a[3] = 1; a[3] <= a.length; a[3]++) {
if (isRepeat(a, 3)) {
continue;
}
if (a[3] == 7 || a[3] == 11) {
continue;
}
for (a[4] = 1; a[4] <= a.length; a[4]++) {
if (isRepeat(a, 4)) {
continue;
}
if (a[4] == 7 || a[4] == 11) {
continue;
}
for (a[5] = 1; a[5] <= a.length; a[5]++) {
if (isRepeat(a, 5)) {
continue;
}
if (a[5] == 7 || a[5] == 11) {
continue;
}
for (a[6] = 1; a[6] <= a.length; a[6]++) {
if (isRepeat(a, 6)) {
continue;
}
if (a[6] == 7 || a[6] == 11) {
continue;
}
for (a[7] = 1; a[7] <= a.length; a[7]++) {
if (isRepeat(a, 7)) {
continue;
}
if (a[7] == 7 || a[7] == 11) {
continue;
}
for (a[8] = 1; a[8] <= a.length; a[8]++) {
if (isRepeat(a, 8)) {
continue;
}
if (a[8] == 7 || a[8] == 11) {
continue;
}
for (a[9] = 1; a[9] <= a.length; a[9]++) {
if (isRepeat(a, 9)) {
continue;
}
if (a[9] == 7 || a[9] == 11) {
continue;
}
int[] l = new int[5];
l[0] = a[5] + a[4] + a[2] + a[9];
l[1] = a[5] + a[1] + a[3] + a[11];
l[2] = a[7] + a[4] + a[1] + a[8];
l[3] = a[7] + a[2] + a[0] + a[11];
l[4] = a[8] + a[3] + a[0] + a[9];
// 判断是否满足规则
if (equry(l)) {
count++;
}
}
}
}
}
}
}
}
}
}
}
// 并且去重,旋转或镜像,所以结果直接除以2就可以了
System.out.println(count/2);
}
private static boolean equry(int[] l) {
for (int i = 0; i < l.length - 1; i++) {
if (l[i] != l[i + 1]) {
return false;
}
}
return true;
}
private static boolean isRepeat(int[] a, int n) {
for (int i = n - 1; i >= 0; i--) {
if (a[i] == a[n]) {
return true;
}
}
return false;
}
}
标题:显示二叉树
排序二叉树的特征是:
某个节点的左子树的所有节点值都不大于本节点值。
某个节点的右子树的所有节点值都不小于本节点值。
为了能形象地观察二叉树的建立过程,小明写了一段程序来显示出二叉树的结构来。
class BiTree
{
private int v;
private BiTree l;
private BiTree r;
public BiTree(int v){
this.v = v;
}
public void add(BiTree the){
if(the.v < v){
if(l==null) l = the;
else l.add(the);
}
else{
if(r==null) r = the;
else r.add(the);
}
}
public int getHeight(){
int h = 2;
int hl = l==null? 0 : l.getHeight();
int hr = r==null? 0 : r.getHeight();
return h + Math.max(hl,hr);
}
public int getWidth(){
int w = (""+v).length();
if(l!=null) w += l.getWidth();
if(r!=null) w += r.getWidth();
return w;
}
public void show(){
char[][] buf = new char[getHeight()][getWidth()];
printInBuf(buf, 0, 0);
showBuf(buf);
}
private void showBuf(char[][] x){
for(int i=0; i
System.out.println();
}
}
private void printInBuf(char[][] buf, int x, int y){
String sv = "" + v;
int p1 = l==null? x : l.getRootPos(x);
int p2 = getRootPos(x);
int p3 = r==null? p2 : r.getRootPos(p2+sv.length());
buf[y][p2] = '|';
for(int i=p1; i<=p3; i++) buf[y+1][i]='-';
for(int i=0; i
if(l!=null) l.printInBuf(buf,x,y+2);
if(r!=null) r.printInBuf(buf,p2+sv.length(),y+2);
}
private int getRootPos(int x){
return l==null? x : x + l.getWidth();
}
}
public class Main
{
public static void main(String[] args)
{
BiTree tree = new BiTree(500);
tree.add(new BiTree(200));
tree.add(new BiTree(509));
tree.add(new BiTree(100));
tree.add(new BiTree(250));
tree.add(new BiTree(507));
tree.add(new BiTree(600));
tree.add(new BiTree(650));
tree.add(new BiTree(450));
tree.add(new BiTree(510));
tree.add(new BiTree(440));
tree.add(new BiTree(220));
tree.show();
}
}
对于上边的测试数据,应该显示出:
|
/--------------500---\
| |
/--200---\ /--509---\
| | | |
100 /--250---\ 507 /--600\
| | | |
220 /--450 510 650
|
440
(如有对齐问题,请参考【图1.png】)
请分析程序逻辑,填写划线部分缺失的代码。
注意,只填写缺少的部分,不要填写已有的代码或符号,也不要加任何说明文字。
答案,阅读代码很难,不过可以通过看图,可以发现:每个数字的开头都对着上一行的一条竖线.所以只需要把数字放到对应直线下的数组上既可以了:所以::::: buf[y+1][p2+i] = sv.charAt(i)
4. 标题:穿越雷区
X星的坦克战车很奇怪,它必须交替地穿越正能量辐射区和负能量辐射区才能保持正常运转,否则将报废。
某坦克需要从A区到B区去(A,B区本身是安全区,没有正能量或负能量特征),怎样走才能路径最短?
已知的地图是一个方阵,上面用字母标出了A,B区,其它区都标了正号或负号分别表示正负能量辐射区。
例如:
A + - + -
- + - - +
- + + + -
+ - + - +
B + - + -
坦克车只能水平或垂直方向上移动到相邻的区。
数据格式要求:
输入第一行是一个整数n,表示方阵的大小, 4<=n<100
接下来是n行,每行有n个数据,可能是A,B,+,-中的某一个,中间用空格分开。
A,B都只出现一次。
要求输出一个整数,表示坦克从A区到B区的最少移动步数。
如果没有方案,则输出-1
例如:
用户输入:
5
A + - + -
- + - - +
- + + + -
+ - + - +
B + - + -
则程序应该输出:
10
资源约定:
峰值内存消耗(含虚拟机) < 512M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
//提示:因为是图的知识,所以进行深搜找到最小值
package sort;
import java.util.Arrays;
import java.util.Scanner;
public class quickSort {
static Scanner scanner = new Scanner(System.in);
static int count = 0;
static int min = -1;
static int a_x, a_y, b_x, b_y;
public static void main(String[] args) {
int n = scanner.nextInt();
String string = scanner.nextLine();
// 输入一个n 代表行数
char[][] cs = new char[n][n];
// 输入一个char[n][n]数组.
for (int i = 0; i < n; i++) {
String Line = scanner.nextLine();
int k = 0;
for (int j = 0; j < Line.length(); j++) {
if (Line.charAt(j) == ' ') {
continue;
}
if (Line.charAt(j) == 'A') {
a_x = i;
a_y = k;
}
if (Line.charAt(j) == 'B') {
b_x = i;
b_y = k;
}
cs[i][k++] = Line.charAt(j);
}
}
boolean[][] bcs = new boolean[n][n];
// 进行深搜, n, cs;
DFS(n, cs, bcs, true, a_x, a_y);
// 按照规格输出结果
System.out.println(min);
}
/**
* 深搜: 搜索条件已经清楚: 必须挨个 + - + -, 找到 B 为结束. 并且不可以向来的方向走,只能 return 到前一步,而不能退回到前一步
* 然后将结果与最小值比较.
*/
private static void DFS(int n, char[][] cs, boolean[][] bcs, boolean flag, int x, int y) {
// 判断周围方格
/**
* 先找 B. 找到就进行比较 count 和 min 然后找周围有无 flag , flag == true 时,找 '+' flag == false
* 时, 找'-' 找到的话,将自己的所在位置对应的boolean值改成 true: 然后进行递归调用.
*/
// 判断周围有无B
count++;
if (judgeB(x, y)) {
// 比较count 和 min
if (min == -1) {
min = count;
} else if (min > count) {
min = count;
}
}
// 按照左右下上的步伐走
if (y - 1 >= 0) {
// 判断可不可以走!
if (bcs[x][y - 1] == false) {
// 判断要不要走!
if (flag == true && cs[x][y - 1] == '+') {
bcs[x][y]=true;
DFS(n, cs, bcs, !flag, x, y - 1);
} else if (flag == false && cs[x][y - 1] == '-') {
bcs[x][y]=true;
DFS(n, cs, bcs, !flag, x, y - 1);
}
}
}
if (y + 1 < n) {
// 判断走过没!
if (bcs[x][y + 1] == false) {
// 判断能不能走!
if (flag == true && cs[x][y + 1] == '+') {
bcs[x][y]=true;
DFS(n, cs, bcs, !flag, x, y + 1);
} else if (flag == false && cs[x][y + 1] == '-') {
bcs[x][y]=true;
DFS(n, cs, bcs, !flag, x, y + 1);
}
}
}
if (x - 1 >= 0) {
// 判断可不可以走!
if (bcs[x - 1][y] == false) {
// 判断要不要走!
if (flag == true && cs[x - 1][y] == '+') {
bcs[x][y]=true;
DFS(n, cs, bcs, !flag, x - 1, y);
} else if (flag == false && cs[x - 1][y] == '-') {
bcs[x][y]=true;
DFS(n, cs, bcs, !flag, x - 1, y);
}
}
}
if (x + 1 < n) {
// 判断可不可以走!
if (bcs[x + 1][y] == false) {
// 判断要不要走!
if (flag == true && cs[x + 1][y] == '+') {
bcs[x][y]=true;
DFS(n, cs, bcs, !flag, x + 1, y);
} else if (flag == false && cs[x + 1][y] == '-') {
bcs[x][y]=true;
DFS(n, cs, bcs, !flag, x + 1, y);
}
}
}
bcs[x][y] = false;
count--;
}
private static boolean judgeB(int x, int y) {
if (b_x == x + 1 || b_x == x - 1) {
if (b_y == y) {
return true;
}
}
if (b_y == y + 1 || b_y == y - 1) {
if (b_x == x) {
return true;
}
}
return false;
}
}
5.
标题:表格计算
某次无聊中, atm 发现了一个很老的程序。这个程序的功能类似于
Excel ,它对一个表格进行操作。
不妨设表格有 n 行,每行有 m 个格子。
每个格子的内容可以是一个正整数,也可以是一个公式。
公式包括三种:
1. SUM(x1,y1:x2,y2) 表示求左上角是第 x1 行第 y1 个格子,右下角
是第 x2 行第 y2 个格子这个矩形内所有格子的值的和。
2. AVG(x1,y1:x2,y2) 表示求左上角是第 x1 行第 y1 个格子,右下角
是第 x2 行第 y2 个格子这个矩形内所有格子的值的平均数。
3. STD(x1,y1:x2,y2) 表示求左上角是第 x1 行第 y1 个格子,右下角
是第 x2 行第 y2 个格子这个矩形内所有格子的值的标准差。
标准差即为方差的平方根。
方差就是:每个数据与平均值的差的平方的平均值,用来衡量单个数据
离开平均数的程度。
公式都不会出现嵌套。
如果这个格子内是一个数,则这个格子的值等于这个数,否则这个格子
的值等于格子公式求值结果。
输入这个表格后,程序会输出每个格子的值。atm 觉得这个程序很好玩
,他也想实现一下这个程序。
「输入格式」
第一行两个数 n, m 。
接下来 n 行输入一个表格。每行 m 个由空格隔开的字符串,分别表示
对应格子的内容。
输入保证不会出现循环依赖的情况,即不会出现两个格子 a 和 b 使得
a 的值依赖 b 的值且 b 的值依赖 a 的值。
「输出格式」
输出一个表格,共 n 行,每行 m 个保留两位小数的实数。
数据保证不会有格子的值超过 1e6。
「样例输入」
3 2
1 SUM(2,1:3,1)
2 AVG(1,1:1,2)
SUM(1,1:2,1) STD(1,1:2,2)
「样例输出」
1.00 5.00
2.00 3.00
3.00 1.48
「数据范围」
对于 30% 的数据,满足: n, m <= 5
对于 100% 的数据,满足: n, m <= 50
资源约定:
峰值内存消耗(含虚拟机) < 512M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多
余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
这题使用到了递归(栈)的知识,每一个方法,里面很可能有其他的方法,所以对应的方法再次求值即可.
求一个函数x1,需要另一个函数B的结果,所以求函数x2的结果,直到最底层的函数x^n找到自己的值.然后返回上一层.
package sort;
import java.text.DecimalFormat;
import java.util.Scanner;
import javax.swing.plaf.nimbus.NimbusLookAndFeel;
public class Main {
/**
* 3,2; 1 SUM(2,1:3,1); 2 AVG(1,1:1,2); SUM(1,1:2,1) STD(1,1:2,2)
*
* @param args
*/
static Scanner scanner = new Scanner(System.in);
public static void main(String[] args) {
// 首先,显而易见.输入问题(,先使用String[], 再使用String[][] 并且使用 split(" ") 分隔符分割开各个数字)
// 不使用空间换时间,而使用递归方法,形成一个简单的栈,遇到公式,就求解公式,公式中的变量中含有公式,就求解公式.
// 为了存储结果,使用一个double[][]数组存储结果,为了更好的使用这个数组,就使用一个boolean[][]数组和一个计算数字的数量.
// 1. 输入
int n, m;
n = scanner.nextInt();
m = scanner.nextInt();
scanner.nextLine(); // 吃掉换行
double[][] num = new double[n][m];
boolean[][] flag_num = new boolean[n][m];
String[] strings = new String[n];
String[][] strs = new String[n][m];
for (int i = 0; i < strings.length; i++) {
strings[i] = scanner.nextLine();
strs[i] = strings[i].split(" ");
}
// 2.遍历一次,将double[][] 和 boolean[][] 初始化.
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (isNum(strs[i][j])) {
num[i][j] = Double.parseDouble(strs[i][j]);
flag_num[i][j] = true;
}
}
}
// 再次遍历,这次通过入栈处理每个公式.
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (flag_num[i][j]) {
continue;
}
qiu_zhi(strs, flag_num, num, i, j);
}
}
for (int i = 0; i < n; i++) {
System.out.print(String.format("%.2f", 1.00 * Math.round(num[i][0] * 100) / 100));
for (int j = 1; j < m; j++) {
System.out.print(" " + String.format("%.2f", (1.00 * Math.round(num[i][j] * 100) / 100)));
}
System.out.println();
}
}
private static void qiu_zhi(String[][] strs, boolean[][] flag_num, double[][] num, int i, int j) {
// 传入的string 一定含有 SUM,AVG,STD 三个字符串
String[] strings1 = strs[i][j].split("\\(");
String[] strings2 = strings1[1].split("\\)");
String[] strings3 = strings2[0].split("\\:");
String[] strings4 = strings3[0].split("\\,");
String[] strings5 = strings3[1].split("\\,");
/*
* 此时 string4 里面是 1:double 2: double string5 1: double 2:double 下面是一个校验.
*/
// for (String string : strings5) {
//
// }
int x1 = Integer.parseInt(strings4[0]);
int y1 = Integer.parseInt(strings4[1]);
int x2 = Integer.parseInt(strings5[0]);
int y2 = Integer.parseInt(strings5[1]);
if (strs[i][j].contains("AVG")) {
AVG(strs, flag_num, num, i, j, x1, y1, x2, y2);
} else if (strs[i][j].contains("SUM")) {
SUM(strs, flag_num, num, i, j, x1, y1, x2, y2);
} else if (strs[i][j].contains("STD")) {
STD(strs, flag_num, num, i, j, x1, y1, x2, y2);
}
flag_num[i][j] = true;
// 判断是哪个公式,知道公式后再进行求值.
// 知道公式后,需要提取四个数字:x1,y1;x2,y2;
// 如果是SUM,直接循环求和
// AVG需要判断有没有自己的情况.
// STD直接求.
}
private static boolean isNum(String string) {
try {
Integer.parseInt(string);
} catch (Exception e) {
// 不是数字会报异常,直接补货异常后进行返回
return false;
}
return true;
}
private static double AVG(String[][] strs, boolean[][] flag_num, double[][] num, int i, int j, int x1, int y1,
int x2, int y2) {
// 求平均数
num[i][j] = AVG(strs, flag_num, num, x1, y1, x2, y2);
return num[i][j];
}
private static double AVG(String[][] strs, boolean[][] flag_num, double[][] num, int x1, int y1, int x2, int y2) {
// 求平均数
int counter = getConter(x1, y1, x2, y2); // 计算总数
return SUM(strs, flag_num, num, x1, y1, x2, y2) / counter;
}
private static double SUM(String[][] strs, boolean[][] flag_num, double[][] num, int x1, int y1, int x2, int y2) {
double sum = 0;
for (int k = x1 - 1; k < x2; k++) {
for (int k2 = y1 - 1; k2 < y2; k2++) {
if (!flag_num[k][k2]) {
qiu_zhi(strs, flag_num, num, k, k2);
}
sum += num[k][k2];
}
}
return sum;
}
private static double SUM(String[][] strs, boolean[][] flag_num, double[][] num, int i, int j, int x1, int y1,
int x2, int y2) {
// 求和
num[i][j] = SUM(strs, flag_num, num, x1, y1, x2, y2);
return num[i][j];
}
private static void STD(String[][] strs, boolean[][] flag_num, double[][] num, int i, int j, int x1, int y1, int x2,
int y2) {
double avg = AVG(strs, flag_num, num, i, j, x1, y1, x2, y2);
double sum_std = 0;
for (int k = x1 - 1; k < x2; k++) {
for (int k1 = y1 - 1; k1 < y2; k1++) {
sum_std += (avg - num[k][k1]) * (avg - num[k][k1]);
}
}
num[i][j] = Math.sqrt((sum_std) / getConter(x1, y1, x2, y2));
}
private static int getConter(int x1, int y1, int x2, int y2) {
// 得到区域内数目总数
return (Math.abs((x2 - x1)) + 1) * (Math.abs(y2 - y1) + 1);
}
}
标题:铺瓷砖
为了让蓝桥杯竞赛更顺利的进行,主办方决定给竞赛的机房重新铺放瓷砖。机房可以看成一个n*m的矩形,而这次使用的瓷砖比较特别,有两种形状,如【图1.png】所示。在铺放瓷砖时,可以旋转。
(图一) 
(图二)
主办方想知道,如果使用这两种瓷砖把机房铺满,有多少种方案。
【输入格式】
输入的第一行包含两个整数,分别表示机房两个方向的长度。
【输出格式】
输出一个整数,表示可行的方案数。这个数可能很大,请输出这个数除以65521的余数。
【样例输入1】
4 4
【样例输出1】
2
【样例说明1】
这两种方案如下【图2.png】所示:
【样例输入2】
2 6
【样例输出2】
4
【数据规模与约定】
对于20%的数据,1<=n, m<=5。
对于50%的数据,1<=n<=100,1<=m<=5。
对于100%的数据,1<=n<=10^15,1<=m<=6。
资源约定:
峰值内存消耗(含虚拟机) < 512M
CPU消耗 < 8000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。