并不NOIP模拟赛

正题

      机房这次来了一次模拟赛，感觉怪怪的。

      考得不怎么样，但是理解好了，给大家说一说。

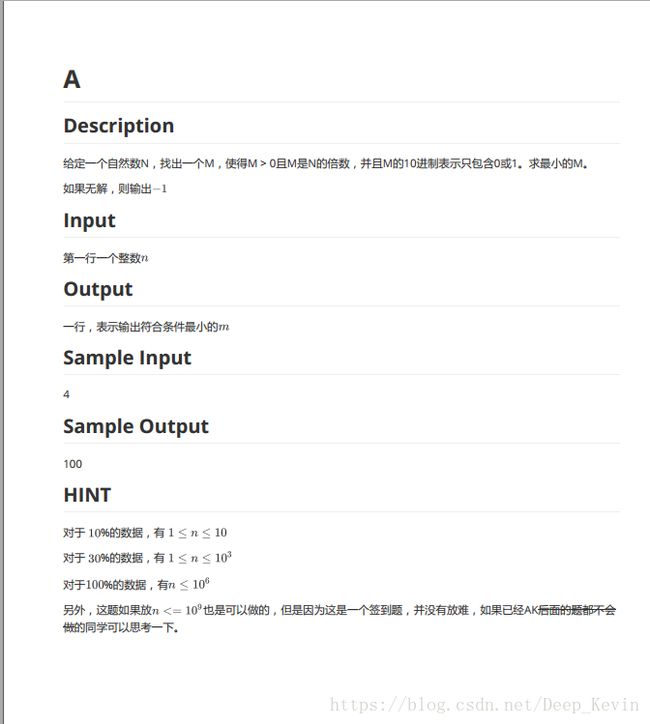
    A题

      

      题面如上

      那么一开始我们肯定先想到是暴力枚举n的倍数m，然后判断其是否为01组成的数。

      但是，其实枚举其倍数需要很高的时间复杂度。

      所以我们换种思路，先枚举01组成的数，再判断其实是否为n的倍数。

      那么我们要保证当前的数最小，显而易见的就想到了广度优先搜索，对于我们枚举过的x，我们选择在其后加上0/1，我们通过用string来存储数，用一个Mod来记录该数对n的Mod值。

      但是遇到极限数据999999，54位的答案依旧会使的做法崩溃。

      所以我们需要加一个优化。

      就是用一个bool数组来记录当前的Mod数是否有出现过，如果出现过，那么不用加入队列，因为前面的数比当前还要小，所以没必要。

代码略丑<请大佬别D0>

#include
#include
#include
#include
#include
using namespace std;

int n;
struct node{
	string x;
	int Mod;
};
queue f;
bool m[1000010];

void bfs(){
	f.push((node){"1",1%n});
	m[1]=true;
	while(!f.empty()){
		node x=f.front();
		f.pop();
		if(x.Mod==0) {
			cout<

      B题

        

      我已经尽力去剪了。。。

      这题很鬼畜，有一种做法就是，建一棵字典树，然后我们把原先m个串丢进去，那么就会最多就会有65535个点()，然后我们把end记录下来，并记录一下每个节点被多少个串经过。

      我们对于新加入的串，在我们建好的字典树中跑dfs，如果现在这个串在这个字典树的第i层（从0开始），我们需要分情况讨论，当这位为0时，那么往0边走，当前的价值要加上对应的w，往1边走不用加，因为相同才要加。当这位为1的时候，就反过来。

       直到当前的价值超过k，那么下面就不可能了， 直接return 0，否则就继续往下搜，直到end， return 当前串的个数就行。

#include
#include
#include
#include
#define lc (now<<1)
#define rc ((now<<1)|1)
using namespace std;

int n,m,q;
int w[20];
char s[20];
int root=1;
bool end[65540];
int tot[65540];
int k;

void add(){
	int now=root;
	for(int i=0;i

      另一种做法是OZY的大写递推。

      首先我们可以猜想一下。

      问题相当于：每位的代价是， 我们现在有一个串，要花费k的代价， 求最多能变化成多少个串的“非”，也就是说能变化成与多少个串每一位不同。

      利用来表示只修改i到n的某些位，现在初始串的状态时j，用k的代价，最多能变化成与多少个串每一位不同。

      我们转移的时候，中间的那一大串英文就是说把j的第i位反过来。

      因为不改，所以你只能选择这位与自己不同的，不需要花费代价。

      然而， 如果需要改，就可以继承这位与自己相同的。

      当然，此时，，够费用才行。

      那么转移就显而易见了，

代码如下

#include
#include
#include
#include
using namespace std;

int n,m,q;
char s[20];
int ci[20];
int cnt[32770];
int f[20][32770][35];
int w[20];
int k=0;

int main(){
	freopen("B.in","r",stdin);
	freopen("B.out","w",stdout);
	scanf("%d %d %d",&n,&m,&q);	
	ci[0]=1;
	for(int i=1;i<=n;i++) ci[i]=ci[i-1]*2;
	for(int i=1;i<=n;i++) scanf("%d",&w[i]);
	for(int i=1;i<=m;i++){
		scanf("%s",s);
		k=0;
		for(int j=0;j=1;now--)
		for(int i=0;i=w[now]) f[now][i][j]+=f[now+1][i][j-w[now]];
			}
	int x;
	for(int i=1;i<=q;i++){
		scanf("%s %d",s,&x);
		k=0;
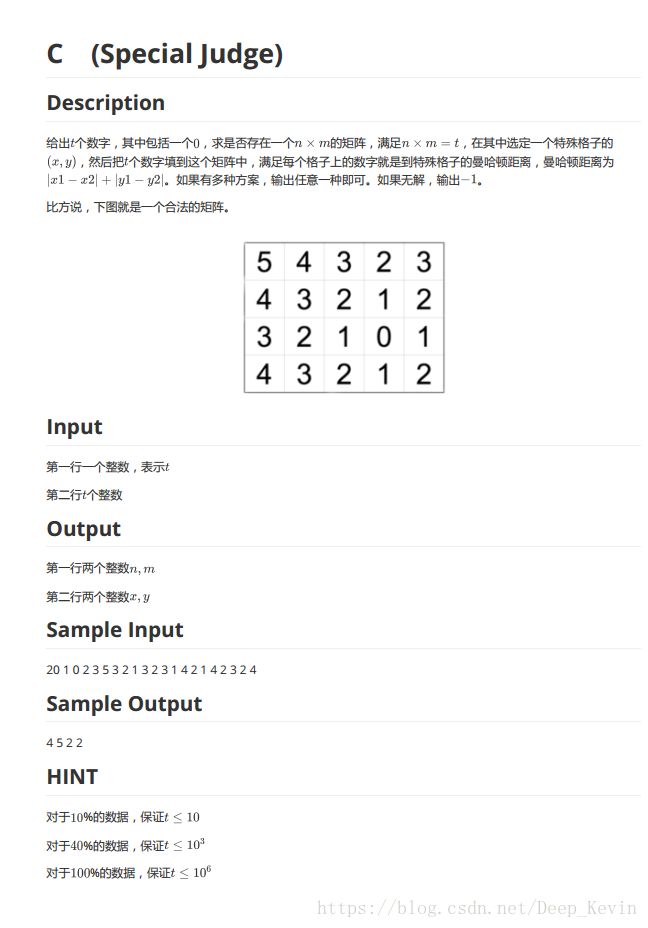
		for(int j=0;j

     C题

      

      这题很有趣。

      要是你暴力的话，那时间复杂度就是，考虑到对折成四分， 可以多除以一个4.

      强行过5个点。。。

      那么我们来试着加优化。首先，肯定可以找到一个最大值，把它放在最上角，，然后我们枚举可能0的位置（斜线），然后不断的判断是否成立，那么复杂度就是约数和*t。优化判-1可以拿到90分。

      然后被OZY暴打。

      其实这个最大值b=n+m-x-y

      所以y=n+m-x-b;

      肯定存在一种方案，使得x是第一个超过边界的值。

      所以我们记录下这个值，分别令x或y等于它，算出另外一个变量的值，判断其是否成立即可。

代码<丑>

#include
#include
#include
#include
#include
using namespace std;

int t;
int tot[1000010];
int now[1000010];
bool tf[1000010];
struct node{
	int x,y,d;
}list[1000010];
int st,ed;
int fx[4]={0,0,-1,1};
int fy[4]={1,-1,0,0};
int mmax=0,mmin;

bool check(int n,int m,int x,int y){
	for(int i=1;i<=t;i++) now[i]=0;
	for(int i=1;i<=t;i++) tf[i]=false;
	tf[(x-1)*m+y]=true;
	st=1,ed=2;
	list[1].x=x;list[1].y=y;list[1].d=0;
	while(st!=ed){
		node x=list[st];
		for(int i=0;i<4;i++){
			int xx=x.x+fx[i],yy=x.y+fy[i];
			if(xx<=0 || xx>n || yy<=0 || yy>m) continue;
			if(tf[(xx-1)*m+yy]==true) continue;
			tf[(xx-1)*m+yy]=true;
			list[ed].x=xx;list[ed].y=yy;list[ed].d=list[st].d+1;
			now[list[ed].d]++;
			if(now[list[ed].d]>tot[list[ed].d]) return false;
			ed++;
		}
		st++;
	}
	return true;
}

int main(){
	freopen("C.in","r",stdin);
	freopen("C.out","w",stdout);
	scanf("%d",&t);
	for(int i=1;i<=t;i++){
		int x;
		scanf("%d",&x);
		tot[x]++;
		if(tot[x]>x*4 && x!=0){
			printf("-1");
			exit(0);
		}
		mmax=max(mmax,x);
	}
	for(int i=1;i<=mmax;i++)
		if(tot[i]t-1){
		printf("-1");
		exit(0);
	}
	for(int i=1;i*i<=t;i++)
		if(t%i==0){
			int j=t/i;
			int x=mmin,y=i+j-x-mmax;
			if(x<=i && y<=j)
				if(check(i,j,x,y)){
					printf("%d %d\n%d %d",i,j,x,y);
					exit(0);
				}
			y=mmin,x=i+j-x-mmax;
			if(x<=i && y<=j)
				if(check(i,j,x,y)){
					printf("%d %d\n%d %d",i,j,x,y);
					exit(0);
				}
		}
	printf("-1");
}

    D题

      

      看上去好像很简单，但其实没什么水法能水过这一题。

      我们先把每一个数都取反，把他丢进一个大bool里面，然后我们从大到小来扫，如果当前枚举的 ，那么我们枚举他的数位，当它其中一个数位为1时，把这位改成0再把新的数丢进布尔。

      最后我们把扫一遍就行了。

      其实它利用的是一种贪心的思想。

      当有一位是1的 时候，另一个串的那一位必须是0，但有一位是0的时候，另一个串的那一位是0还是1无所谓，但是就是因为这个无所谓，问题才变得棘手。

      如果把问题转化为“是否有多少个串与该串每一位都不同”，那么就容易多了。

      所以就是利用这个思想，我们先取反，再考虑可分支的状态，因为某一位是0的时候，另一个串是0还是1无所谓，所以在取反的时候可以把1改成0，如果可以匹配上，就是说有一个串该位是0，所以对于它来说，1还是0在取反串还是原串无所谓。

      但不能把0改1，因为在原串中相当于把1改成0，明显是不行的，因为原来&值不为0。

      我也不知道说清楚没有，好好想想吧，我尽力了。

#include
#include
#include
using namespace std;

int n;
int op=1048575;
bool tf[1048580];
int a[1000010];

int main(){
	freopen("D.in","r",stdin);
	freopen("D.out","w",stdout);
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		tf[a[i]^op]=true;
	}
	for(int i=op;i>=0;i--)
		for(int k=0;k<=19;k++)
			if((i&(1<