2015年javaB组蓝桥杯
2.立方变自身
观察下面的现象,某个数字的立方,按位累加仍然等于自身。
1^3 = 1
8^3 = 512 5+1+2=8
17^3 = 4913 4+9+1+3=17
...
请你计算包括1,8,17在内,符合这个性质的正整数一共有多少个?
请填写该数字,不要填写任何多余的内容或说明性的文字。6
public class Main {
public static void main(String[] args){
int count = 0;
for(int i = 1;i < 500;i ++){
int lifang = (int) Math.pow(i, 3);
if(qushuwei(lifang) == i){
count++;
}
}
System.out.print(count);
}
private static int qushuwei(int lifang) {
// TODO Auto-generated method stub
int a = lifang%10;
int sum = a;
while(lifang/10 !=0){
int b = lifang/10%10;
lifang = lifang/10;
sum = sum+b;
}
return sum;
}
}(1)经过分析可以判断出满足这个条件的整数肯定在500以内,当然还可以再缩小一下范围,这不是很重要啦,数据不是很多。
(2)本题目的关键在于取位数,使用while循环
3.三羊献瑞
观察下面的加法算式:
祥 瑞 生 辉
+ 三 羊 献 瑞
-------------------
三 羊 生 瑞 气
(如果有对齐问题,可以参看【图1.jpg】)
其中,相同的汉字代表相同的数字,不同的汉字代表不同的数字。
请你填写“三羊献瑞”所代表的4位数字(答案唯一),不要填写任何多余内容。1085
public class Main {
public static void main(String[] args){
int a=0,b=0,c=0,d=0,e=0,f=0,g=0,h=0;
for(a = 1;a < 10;a++){
for(b = 0;b < 10;b++){
for(c = 0;c < 10;c++){
for(d = 0;d < 10;d++){
for(e = 1;e < 10;e++){
for(f = 0;f < 10;f++){
for(g = 0;g < 10;g++){
for(h = 0;h < 10;h++){
int i = a*1000+b*100+c*10+d;
int j = e*1000+f*100+g*10+b;
int k = e*10000+f*1000+c*100+b*10+h;
if(a!=b && a!=c && a!=d && a!=e && a!=f && a!=g && a!=h
&& b!=c && b!=d && b!=e && b!=f && b!=g && b!=h
&& c!=d && c!=e && c!=f && c!=g && c!=h
&& d!=e && d!=f && d!=g && d!=h
&& e!=f && e!=g && e!=h
&& f!=g && f!=h
&& g!=h&&(i + j == k)){
System.out.println(j);
}
}
}
}
}
}
}
}
}
}
}直接使用暴力循环,注意题目中的要求,不要漏掉判断条件。
回溯法有通用解题法之称,它可以系统的搜索一个问题的所有解或者任意解。它在问题的解空间树中,按深度优先策略从根节点出发搜索解空间树,算法搜索至解空间树的任意一个结点时,先判断该节点如(子树)是否包含问题的解,如果肯定不包含,则跳过对其子树的搜索,逐层向其根节点回溯。否则,则按照深度优先的策略搜索子树。
当回溯到根,且根节点的所有子树都已被搜索遍才结束。这种以深度优先方式系统搜索问题解的算法称为回溯法,适用于解决组合数较大的问题。
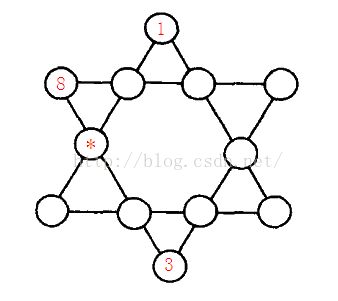
4.六角填数
如图【1.png】所示六角形中,填入1~12的数字。使得每条直线上的数字之和都相同。
图中,已经替你填好了3个数字,请你计算星号位置所代表的数字是多少?
请通过浏览器提交答案,不要填写多余的内容。
public class Main {
static int []a = new int[15];
static int []visit = new int[15];
public static void main(String[] args){
a[0] = 1;
a[1] = 8;
a[11] = 3;
visit[1] = 1;
visit[8] = 1;
visit[3] = 1;
dfs(0);
}
private static void dfs(int x) {
// TODO Auto-generated method stub
if(x == 0||x == 1||x == 11){
dfs(x+1);
return;
}
if(x == 12){
int []b = new int[6];
b[0] = a[0]+a[2]+a[5]+a[7];
b[1] = a[0]+a[3]+a[6]+a[10];
b[2] = a[1]+a[2]+a[3]+a[4];
b[3] = a[1]+a[5]+a[8]+a[11];
b[4] = a[4]+a[6]+a[9]+a[11];
b[5] = a[7]+a[8]+a[9]+a[10];
for(int i = 1;i < 6;i++){
if(b[i-1] != b[i])
return;
}
System.out.print(a[5]);
return;
}
for(int i = 2;i < 13;i++){
if(visit[i] == 0){
visit[i] = 1;
a[x] = i;
dfs(x+1);
visit[i] = 0;
}
}
}
}如果用暴力,未知量的个数比较多,条件太复杂,此路不通。采用深度优先算法,dfs(int x)中间的x表示初始节点。
return;上面的return语句用于终止方法并返回到方法的调用者,可以改变void方法中的正常流程控制。
5.五星填数
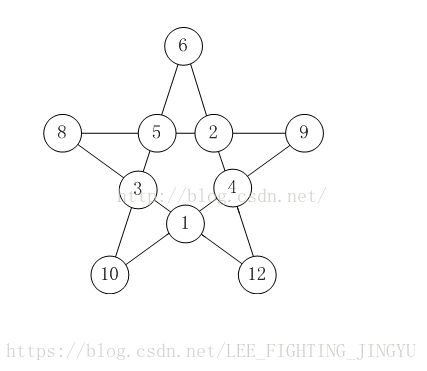
如【图1.png】的五星图案节点填上数字:1~12,除去7和11。
要求每条直线上数字和相等。
如图就是恰当的填法。
请你利用计算机搜索所有可能的填法有多少种。
注意:旋转或镜像后相同的算同一种填法。
请提交表示方案数目的整数,不要填写任何其它内容。
 12
12
public class Main {
static int []a = new int[15];
static int []visit = new int[15];
static int sum ;
static int []f = {1,2,3,4,5,6,8,9,10,12};
public static void main(String[] args){
dfs(0);
System.out.println(sum/5/2);
}
private static void dfs(int x) {
// TODO Auto-generated method stub
int []b = new int[5];
b[0] = a[0]+a[2]+a[5]+a[8];
b[1] = a[0]+a[3]+a[6]+a[9];
b[2] = a[1]+a[2]+a[3]+a[4];
b[3] = a[1]+a[5]+a[7]+a[9];
b[4] = a[4]+a[6]+a[7]+a[8];
if(x == 10){
if(b[0] == b[1] && b[0] ==b[2] && b[0]==b[3] && b[0]==b[4]){
sum++;
}
return;
}
for(int i = 0;i < f.length;i++){
if(visit[f[i]] == 0){
visit[f[i]] = 1;
a[x] = f[i];
dfs(x+1);
visit[f[i]] = 0;
}
}
}
}
采用深度优先算法,最后去除镜像/2,取出旋转/5
6.标题:纸牌三角形
A,2,3,4,5,6,7,8,9 共9张纸牌排成一个正三角形(A按1计算)。要求每个边的和相等。
下图就是一种排法(如有对齐问题,参看p1.png)。
A
9 6
4 8
3 7 5 2
这样的排法可能会有很多。
如果考虑旋转、镜像后相同的算同一种,一共有多少种不同的排法呢?
请你计算并提交该数字。
注意:需要提交的是一个整数,不要提交任何多余内容。144
public class Main {
static int []a = new int[12];
static int []visit = new int[12];
static int sum = 0 ;
public static void main(String[] args){
dfs(0);
System.out.println(sum/2/3);
}
private static void dfs(int x) {
// TODO Auto-generated method stub
int []b = new int[4];
b[0] = a[0]+a[1]+a[3]+a[5];
b[1] = a[0]+a[2]+a[4]+a[8];
b[2] = a[5]+a[6]+a[7]+a[8];
if(x == 9){
if(b[0] == b[1]&&b[0]==b[2])
sum++;
return;
}
for(int i = 1;i < 10;i++){
if(visit[i] == 0){
visit[i] = 1;
a[x] = i;
dfs(x+1);
visit[i] = 0;
}
}
}
}100 可以表示为带分数的形式:100 = 3 + 69258 / 714。
还可以表示为:100 = 82 + 3546 / 197。
注意特征:带分数中,数字1~9分别出现且只出现一次(不包含0)。
类似这样的带分数,100 有 11 种表示法。
从标准输入读入一个正整数N (N<1000*1000)
程序输出该数字用数码1~9不重复不遗漏地组成带分数表示的全部种数。
注意:不要求输出每个表示,只统计有多少表示法!
建造剪枝条件:
(1)n=n1+n2/n3;
(2)首先n1一定是小于n的:n1
(3)因为n为整数,n1为整数,所以n2/n3也应为整数,这就要求n2/n3一定可以整除,即n2%n3==0;
(4)n2/n3还要满足可除条件,即n2>=n3。
在1至9的全排列(9个数字)中确定n1,n2,n3的取值范围:
(1)n1能从第1位,取到第7位,肯定取不到第8和第9位。
(2)n2>=n3,则n2的取值范围一定在n1选择后,选择剩下的一半或一半以上的数据。
举个例子,1至9的其中一个全排列--156987423,若n1选择156,则n2只能选择剩下的987423中的一半或
一半以上,如987、9874、98742,如果n2小于剩下的一半,则不满足条件。
(3)n3的范围则是n1和n2选择剩下的所有了。
如果n1选择9位中的前i位,那么n2的结尾j选择范围为第i+(9-i+1)/2至第8位数字,n3是从第j位至第9位。
利用深度优先搜索(得到一个9位的全排列)和适当的判断(剪枝,找出符合4个条件的全排列)就可以解决。
import java.util.Scanner;
public class Main {
static int []a = {1,2,3,4,5,6,7,8,9};
static int []visit = new int[10];
static int n,n1,n2,n3;
static int count = 0;
public static void main(String[] args){
Scanner input = new Scanner(System.in);
n = input.nextInt();
if(n < 1000000 && n > 0){
dfs(0);
System.out.println(count);
}
}
private static int sum(int begin, int end) {
int k = 0;
for(int i = begin;i <= end ;i++)
k = k*10 + a[i];
return k;
}
private static void dfs(int x) {
if(x == 9){
for(int i = 0;i <= 5;i++){
n1= sum(0,i);
if(n1 >= n)
break;
for(int j = i+(10-i)/2;j <= 7;j++){
n2 = sum(i+1,j);
n3 = sum(j+1,8);
if(n2>=n3 && n2%n3==0 && n==n1+n2/n3){
count++;
}
}
}
return;
}
for(int i = 1; i <= 9;i++){
if(visit[i] == 0){
visit[i] = 1;
a[x] = i;
dfs(x+1);
visit[i] = 0; }
}
}
}上面贴出的代码一直不能AC,希望大神指点迷津。
8.剪格子
如下图所示,3 x 3 的格子中填写了一些整数。
|10* 1|52|
+--****--+
|20|30* 1|
*******--+
| 1| 2| 3|
+--+--+--+
我们沿着图中的星号线剪开,得到两个部分,每个部分的数字和都是60。
本题的要求就是请你编程判定:对给定的m x n 的格子中的整数,是否可以分割为两个部分,使得这两个区域的数字和相等。
如果存在多种解答,请输出包含左上角格子的那个区域包含的格子的最小数目。
如果无法分割,则输出 0。
程序先读入两个整数 m n 用空格分割 (m,n<10)。
表示表格的宽度和高度。
接下来是n行,每行m个正整数,用空格分开。每个整数不大于10000。
10 1 52
20 30 1
1 2 3
1 1 1 1
1 30 80 2
1 1 1 100
import java.util.Scanner;
public class Main {
static int [][]f = new int[20][20];
static int [][]visit = new int[20][20];
static int fx[] = {1,-1,0,0};
static int fy[] = {0,0,-1,1};
static int n,m;
static int sum = 0;
static int minOfCount = 121;//将可能存在的最大的格子数输入
public static void main(String[] args){
Scanner input = new Scanner(System.in);
n = input.nextInt();//行数
m = input.nextInt();//列数
for(int i = 0;i < n ; i++){
for(int j = 0;j < m ;j++){
f[i][j] = input.nextInt();
sum += f[i][j];
}
}
if(sum%2 != 0){
System.out.println(0);
}
sum = sum/2;
visit[0][0] = 1;
dfs(0,0,f[0][0],1);//从(0,0)点开始搜索
if(minOfCount == 121)
System.out.println(0);
else
System.out.println(minOfCount);
}
//x,y表示当前搜索起点的坐标
//total表示当前搜索位置的和
//count表示到当前搜索位置的格子个数
private static void dfs(int x,int y,int total,int count) {
if(total > sum)//和超过sum之后要进行回溯
return;
if(total == sum){//输出最小的格子个数,是出口
minOfCount = Math.min(minOfCount, count);
return;
}
for(int i = 0;i < 4;i++){
int xx = x + fx[i];
int yy = y + fy[i];
if(xx>=0 && xx=0 && yy 注意:题目要求先输入列数,再输入行数,这是个陷阱!!!
将格子分为两部分,为了保证得到包括左上角格子部分的最小格子个数,我们可以直接从(0,0)点开始想四个方向进行深搜,直到搜索到格子数等于总格子数和的一半大小,找到出口。
在这里,我们一开始需要给minOfCount赋初值,为题目允许的最大的格子数,否则会一直输出为0
上面贴出的代码没有AC,请求大神指点迷津。
9.标题:方格分割
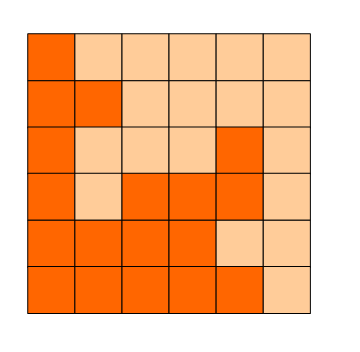
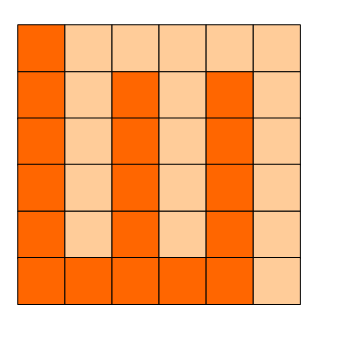
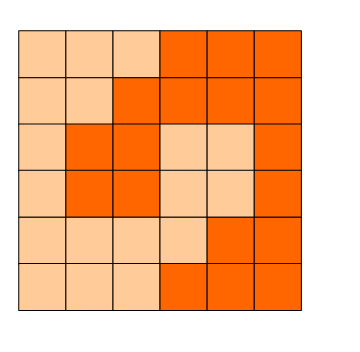
6x6的方格,沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。
如图:p1.png, p2.png, p3.png 就是可行的分割法。
包括这3种分法在内,一共有多少种不同的分割方法。
注意:旋转对称的属于同一种分割法。
请提交该整数,不要填写任何多余的内容或说明文字。509
public class Main {
static int [][]f = new int[10][10];
static int [][]visit = new int[10][10];
static int fx[] = {1,0,-1,0};
static int fy[] = {0,-1,0,1};
static int count = 0;
public static void main(String[] args){
visit[3][3] = 1;
dfs(3,3);
System.out.println(count/4);
}
private static void dfs(int x, int y){
if(x == 0 || x == 6 || y == 0 || y == 6){
count++;
return;
}
for(int i = 0;i < 4;i++){
int x1 = x + fx[i];
int y1 = y + fy[i];
int x2 = 6 - x1;
int y2 = 6 - y1;
if(x1>=0 && x1<7 && y1>=0 && y1<7 && visit[x1][y1]==0){
visit[x1][y1] = 1;
visit[x2][y2] = 1;
dfs(x1,y1);
visit[x1][y1] = 0;
visit[x2][y2] = 0;
}
}
}
}
(3,3)是分界线的中心对称点,我们从(3,3)出发,向两个方向同时进行深搜,当到达x或者y的边界的时候即为出口;
由于旋转对称属于同一种分割方法,所以结果为count除以4。
概念引申:把一个图形绕一个定点旋转一个角度后,与初始图形重合,即为旋转对称。旋转角大于0度,小于360度。
把一个图形绕着一个定点旋转180度后,与初始图形重合,即为中心对称,是旋转角为180度的特殊的旋转对称。
10.九宫重排

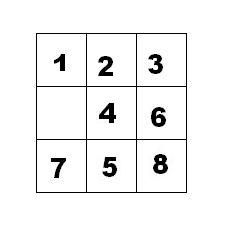
我们把第一个图的局面记为:12345678.
把第二个图的局面记为:123.46758
显然是按从上到下,从左到右的顺序记录数字,空格记为句点。
本题目的任务是已知九宫的初态和终态,求最少经过多少步的移动可以到达。如果无论多少步都无法到达,则输出-1。
123.46758
46758123.
11.李白打酒
话说大诗人李白,一生好饮。幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒2斗。他边走边唱:
无事街上走,提壶去打酒。
逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店5次,遇到花10次,已知最后一次遇到的是花,他正好把酒喝光了。
请你计算李白遇到店和花的次序,可以把遇店记为a,遇花记为b。则:babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢?请你计算出所有可能方案的个数(包含题目给出的)。
注意:通过浏览器提交答案。答案是个整数。不要书写任何多余的内容。14
public class Main {
static int count = 0;
public static void main(String[] args){
dfs(0,0,2);
System.out.println(count);
}
private static void dfs(int a,int b ,int sum) {
if(sum < 0)
return;
if(a == 5 && b == 8 && sum == 2)
count++;
if(a < 5)
dfs(a+1,b,sum*2);
if(b < 10)
dfs(a,b+1,sum-1);
}
}比较简单的深搜使用,单纯的递归,只要找到满足条件的出口就可以。
12.循环节长度
两个整数做除法,有时会产生循环小数,其循环部分称为:循环节。比如,11/13=6=>0.846153846153..... 其循环节为[846153] 共有6位。下面的方法,可以求出循环节的长度。请仔细阅读代码,并填写划线部分缺少的代码。
注意,只能填写缺少的部分,不要重复抄写已有代码。不要填写任何多余的文字。6
import java.util.Vector;
public class Main {
public static void main(String[] args){
System.out.println(f(11,13));
}
public static int f(int n, int m)
{
n = n % m;
Vector v = new Vector();
for(;;)
{
v.add(n);
n *= 10;
n = n % m;
if(n==0) return 0;
if(v.indexOf(n)>=0)
return v.size() - v.indexOf(n); //填空
}
}
}
v.indexOf(n)返回参数第一次出现的索引。
v.size()返回向量中的组件数。组件数依次为:11、6、8、2、7、5、11、6、8......
由此可见当11出现时,此时第一次循环已经结束,可以确定循环节的长度,为v.size()-v.indexOf(n);
13.九数组分数
1,2,3...9 这九个数字组成一个分数,其值恰好为1/3,如何组法?下面的程序实现了该功能,请填写划线部分缺失的代码。
注意,只能填写缺少的部分,不要重复抄写已有代码。不要填写任何多余的文字。5832 17496 5823 17469
public class Main {
public static void test(int[] x)
{
int a = x[0]*1000 + x[1]*100 + x[2]*10 + x[3];
int b = x[4]*10000 + x[5]*1000 + x[6]*100 + x[7]*10 + x[8];
if(a*3==b) System.out.println(a + " " + b);
}
public static void f(int[] x, int k)
{
if(k>=x.length){
test(x);
return;
}
for(int i=k; i典型的全排列问题,通过枚举出1~9的全排列,从中找出符合条件的排列输出,深度搜索在全局变量回溯完成后必须变回初值。
算是一个常识性的问题了。
我们都知道:1+2+3+ ... + 49 = 1225 现在要求你把其中两个不相邻的加号变成乘号,使得结果为2015
比如:1+2+3+...+10*11+12+...+27*28+29+...+49 = 2015 就是符合要求的答案。
请你寻找另外一个可能的答案,并把位置靠前的那个乘号左边的数字提交(对于示例,就是提交10)。
注意:需要你提交的是一个整数,不要填写任何多余的内容。
10 27
16 24
24 16
27 10public class Main {
public static void main(String[] args){
for(int i = 1;i < 47;i++){
int firstResult = i*(i+1);//第一个乘号只能从1*2 到46*47中选择
for(int j = 3;j < 49;j++){
int secondResult = j*(j+1); //第二个乘号只能从3*4 到48*49中选择
if((1225-i-i-1-j-j-1+firstResult + secondResult) == 2015){
System.out.println(i + " " + j);
}
}
}
}
}小明被劫持到X赌城,被迫与其他3人玩牌。一副扑克牌(去掉大小王牌,共52张),均匀发给4个人,每个人13张。
这时,小明脑子里突然冒出一个问题:如果不考虑花色,只考虑点数,也不考虑自己得到的牌的先后顺序,自己手里能拿到的初始牌型组合一共有多少种呢?请填写该整数,不要填写任何多余的内容或说明文字。3598180
思路:循环遍历每个点数所选择的张数,最多4张,最少0张,每当牌的总数达到13张则计数。
方法一:暴力
public class Main {
public static void main(String[] args){
int []a = new int[13];
int count = 0;
for(a[0]=0; a[0]<=4; a[0]++)
for(a[1]=0; a[1]<=4; a[1]++){
for(a[2]=0; a[2]<=4; a[2]++){
for(a[3]=0; a[3]<=4; a[3]++){
for(a[4]=0; a[4]<=4; a[4]++){
for(a[5]=0; a[5]<=4; a[5]++){
for(a[6]=0; a[6]<=4; a[6]++){
for(a[7]=0; a[7]<=4; a[7]++){
for(a[8]=0; a[8]<=4; a[8]++){
for(a[9]=0; a[9]<=4; a[9]++){
for(a[10]=0; a[10]<=4; a[10]++){
for(a[11]=0; a[11]<=4; a[11]++){
for(a[12]=0; a[12]<=4; a[12]++){
if(a[0]+a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]+a[9]+a[10]+a[11]+a[12]==13){
count++;
}
}
}
}
}
}
}
}
}
}
}
}
}
System.out.println(count);
}
}方法二:深搜
public class Main {
static int sum = 0;//手中牌的总张数
static int count = 0;//方案的个数
public static void main(String[] args){
dfs(1);
System.out.println(count);
}
private static void dfs(int x) {//x表示当前手中牌的数字
if(sum > 13)
return;
if(sum == 13 && x == 14){//牌型搜索完毕且恰好有13张牌
count++;
return;
}
if(x < 14){
for(int i = 0;i <= 4;i++){
sum = sum+i;
dfs(x+1);
sum = sum -i;//回溯完成后要将sum变回原数值
}
}
}
}
乐羊羊饮料厂正在举办一次促销优惠活动。乐羊羊C型饮料,凭3个瓶盖可以再换一瓶C型饮料,并且可以一直循环下去,但不允许赊账。请你计算一下,如果小明不浪费瓶盖,尽量地参加活动,那么,对于他初始买入的n瓶饮料,最后他一共能得到多少瓶饮料。
输入:一个整数n,表示开始购买的饮料数量(0
例如:
用户输入:
100
程序应该输出:
149
用户输入:
101
程序应该输出:
151
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
import java.util.Scanner;
public class Main {
public static void main(String[] args){
Scanner input = new Scanner(System.in);
int numOfBottle = input.nextInt();
int sum = numOfBottle;
if(numOfBottle == 1 || numOfBottle == 2)
sum = numOfBottle;
while(numOfBottle >= 3){
int drinked = numOfBottle - numOfBottle%3;
int get = numOfBottle/3;
numOfBottle = numOfBottle - drinked + get;
sum = sum + get;
}
System.out.println(sum);
}
}17.垒骰子
赌圣atm晚年迷恋上了垒骰子,就是把骰子一个垒在另一个上边,不能歪歪扭扭,要垒成方柱体。经过长期观察,atm 发现了稳定骰子的奥秘:有些数字的面贴着会互相排斥!我们先来规范一下骰子:1 的对面是 4,2 的对面是 5,3 的对面是 6。
假设有 m 组互斥现象,每组中的那两个数字的面紧贴在一起,骰子就不能稳定的垒起来。 atm想计算一下有多少种不同的可能的垒骰子方式。两种垒骰子方式相同,当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。
由于方案数可能过多,请输出模 10^9 + 7 的结果。不要小看了 atm 的骰子数量哦~
「输入格式」
第一行两个整数 n m
n表示骰子数目
接下来 m 行,每行两个整数 a b ,表示 a 和 b 不能紧贴在一起。
「输出格式」
一行一个数,表示答案模 10^9 + 7 的结果。
「样例输入」
2 1
1 2
「样例输出」
544
「数据范围」
对于 30% 的数据:n <= 5
对于 60% 的数据:n <= 100
对于 100% 的数据:0 < n <= 10^9, m <= 36
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
18.生命之树
在X森林里,上帝创建了生命之树。他给每棵树的每个节点(叶子也称为一个节点)上,都标了一个整数,代表这个点的和谐值。上帝要在这棵树内选出一个非空节点集S,使得对于S中的任意两个点a,b,都存在一个点列 {a, v1, v2, ..., vk, b} 使得这个点列中的每个点都是S里面的元素,且序列中相邻两个点间有一条边相连。在这个前提下,上帝要使得S中的点所对应的整数的和尽量大。这个最大的和就是上帝给生命之树的评分。经过atm的努力,他已经知道了上帝给每棵树上每个节点上的整数。但是由于 atm 不擅长计算,他不知道怎样有效的求评分。他需要你为他写一个程序来计算一棵树的分数。
「输入格式」
第一行一个整数 n 表示这棵树有 n 个节点。
第二行 n 个整数,依次表示每个节点的评分。
接下来 n-1 行,每行 2 个整数 u, v,表示存在一条 u 到 v 的边。由于这是一棵树,所以是不存在环的。
「输出格式」
输出一行一个数,表示上帝给这棵树的分数。
「样例输入」
5
1 -2 -3 4 5
4 2
3 1
1 2
2 5
「样例输出」
8
「数据范围」
对于 30% 的数据,n <= 10
对于 100% 的数据,0 < n <= 10^5, 每个节点的评分的绝对值不超过 10^6 。
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 3000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
待更。。。。。。