重温数据结构:二叉树的常见问题汇总
最近复习数据结构,自己将二叉树的常见问题写了一篇。部分代码参考了如下博文:
1.http://blog.csdn.net/fightforyourdream/article/details/16843303
2.http://blog.csdn.net/luckyxiaoqiang/article/details/7518888
解决的常见问题为:
1. 求二叉树中的节点个数
2. 求二叉树的深度
3. 前序遍历,中序遍历,后序遍历
4. 分层遍历二叉树
5. 将二叉查找树变为有序的双向链表
6. 求二叉树第K层的节点个数
7. 求二叉树中叶子节点的个数
8. 求二叉树的镜像
9.由前序遍历序列和中序遍历序列重建二叉树
10.判断二叉树是不是完全二叉树
11.获取任意节点与根节点的路径
12. 求二叉树中两个节点的最低公共祖先节点
13.求二叉树的宽度
14.判断二叉树是否是AVL树(平衡二叉树)
源代码如下:
package edu.njupt.zhb;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Stack;
import java.util.concurrent.LinkedBlockingDeque;
import java.util.concurrent.LinkedBlockingQueue;
/*
*@author: ZhengHaibo
*web: http://blog.csdn.net/nuptboyzhb
*mail: [email protected]
*2014-3-13 Nanjing,njupt,China
*/
/**
* 二叉树的实现
*/
public class MyBinaryTree {
/**
* 二叉树的节点
*/
public class TreeNode{
Object data;//数据区
TreeNode left;//左子树
TreeNode right;//右子树
}
public MyBinaryTree(){
}
/**
* 先序遍历的递归实现
* 根->左子树->右子树
* @param root
* @param list
*/
public void preOrderTraverse(TreeNode root,List list){
if(root==null){
return;
}
list.add(root.data);
preOrderTraverse(root.left, list);
preOrderTraverse(root.right, list);
}
/**
* 先序遍历的非递归实现,借助单栈
* @param root
* @param list
*/
public void preOrderLoop(TreeNode root,List list){
if(root==null){
return;
}
Stack stack = new Stack();
stack.push(root);
while(!stack.isEmpty()){
TreeNode node = stack.pop();
list.add(node.data);
if(node.right!=null){//如果右子树不为空,入栈
stack.push(node.right);
}
if(node.left!=null){////如果左子树不为空,入栈
stack.push(node.left);
}
}
}
/**
* 中序遍历的递归实现
* 左子树->根->右子树
* @param root
* @param list
*/
public void inOrderTraverse(TreeNode root,List list){
if(root==null){
return;
}
inOrderTraverse(root.left, list);
list.add(root.data);
inOrderTraverse(root.right, list);
}
/**
* 中序遍历的非递归实现(双栈)
* 左子树->根->右子树
* @param root
* @param list
*/
public void inOrderLoop(TreeNode root,List list){
if(root==null){
return ;
}
Stack stack = new Stack();
TreeNode pNode=root;
while(pNode!=null||!stack.isEmpty()){
while(pNode!=null){//一直将该节点的左子树入栈
stack.push(pNode);
pNode=pNode.left;
}
if(!stack.isEmpty()){
pNode=stack.pop();
list.add(pNode.data);
pNode=pNode.right;//转向右子树进行下一次循环
}
}
}
/**
* 后序遍历的递归实现
* 左子树->右子树->根
* @param root
* @param list
*/
public void postOrderTraverse(TreeNode root,List list){
if(root==null){
return;
}
postOrderTraverse(root.left, list);
postOrderTraverse(root.right, list);
list.add(root.data);
}
public void postOrderTraverse2(TreeNode root,List list){
if(root==null){
return;
}
postOrderTraverse2(root.left, list);
postOrderTraverse2(root.right, list);
list.add(root);
}
/**
* 后序编列的非递归方式(双栈法)
* 后序遍历为:左子树->右子树->根节点
* 然而,我们知道,前序遍历的非递归方式非常容易实现。我们倒着输出
* 根节点->右子树->左子树的方式就是后序遍历。而根节点->右子树->左子树的
* 非递归实现和前序遍历的非递归实现非常相似,只是颠倒一下左右子树的顺序
* @param root
* @param list
*/
public void postOrderLoop(TreeNode root,List list){
if(root==null){
return;
}
Stack stack = new Stack();//用于遍历
Stack output = new Stack();//用于保存逆序
stack.push(root);
while (!stack.isEmpty()) {
TreeNode treeNode = stack.pop();
output.push(treeNode);
if(treeNode.left!=null){//先将左子树入栈
stack.push(treeNode.left);
}
if(treeNode.right!=null){//再将右子树入栈
stack.push(treeNode.right);
}
}
/**
* 将output栈中的数据放入list中即可完成了反转
*/
while(!output.isEmpty()){
list.add(output.pop().data);
}
}
// public void postOrderLoop(TreeNode root,List list){
// if(root==null){
// return;
// }
// TreeNode pNode=root;
// Stack stack=new Stack();
// while(pNode!=null||!stack.isEmpty()){
// while(pNode!=null){//左右不断深入
// stack.push(pNode);//先将根节点入栈
// if(pNode.left!=null){
// pNode=pNode.left;
// }else {
// pNode=pNode.right;
// }
// }
// if(!stack.isEmpty()){
// pNode=stack.pop();//取出栈顶根节点,访问之
// list.add(pNode.data);
// }
// //满足条件时,说明栈顶根节点右子树已经访问,应出栈访问之
// while(!stack.isEmpty()&&stack.peek().right.equals(pNode)){
// pNode=stack.pop();
// list.add(pNode.data);
// }
// //转向栈顶根节点的右子树继续后续遍历
// if(!stack.isEmpty()){
// pNode=stack.peek().right;
// }else {
// pNode=null;
// }
// }
// }
/**
* 层次遍历
* @param root
* @param list
*/
public void levelOrderTraverse(TreeNode root,List list){
if(root==null){
return;
}
Queue queue = new LinkedBlockingDeque();
queue.add(root);
while(!queue.isEmpty()){
TreeNode node = (TreeNode)queue.remove();
list.add(node.data);
if(node.left!=null){
queue.add(node.left);
}
if(node.right!=null){
queue.add(node.right);
}
}
}
/**
* 获取二叉树中节点的个数
* 递归解法:
* (1)如果二叉树为空,节点个数为0
* (2)如果二叉树不为空,二叉树节点个数 = 左子树节点个数 + 右子树节点个数 + 1
* @param root
* @return
*/
public int getNodeNum(TreeNode root){
if(root==null){
return 0;
}
return getNodeNum(root.left)+getNodeNum(root.right)+1;
}
/**
* 求二叉树第K层的节点个数
* 递归解法:
* (1)如果二叉树为空或者k<1返回0
* (2)如果二叉树不为空并且k==1,返回1
* (3)如果二叉树不为空且k>1,返回k-1层中左子树的节点个数与右子树节点个数之和
* @param root
* @param k
* @return
*/
public int getKthNodeNum(TreeNode root,int k){//*
if(root==null||k<1){
return 0;
}
if(k==1){
return 1;
}
int leftNum = getKthNodeNum(root.left, k-1);
int rightNum = getKthNodeNum(root.right, k-1);
return leftNum+rightNum;
}
/**
* 求二叉树中叶子节点的个数
* 递归解法:
* (1)如果二叉树为空,返回0
* (2)如果二叉树不为空且左右子树为空,返回1
* (3)如果二叉树不为空,且左右子树不同时为空,返回左子树中叶子节点个数加上右子树中叶子节点个数
* @param root
* @return
*/
public int getLeafNodeNum(TreeNode root){
if(root==null){
return 0;
}
if(root.left==null&&root.right==null){
return 1;
}
int leftNum = getLeafNodeNum(root.left);
int rightNum = getLeafNodeNum(root.right);
return leftNum+rightNum;
}
/**
* 求二叉树的镜像
* 递归解法:
* (1)如果二叉树为空,返回空
* (2)如果二叉树不为空,求左子树和右子树的镜像,然后交换左子树和右子树
* @param root
* @return
*/
public TreeNode mirrorTree(TreeNode root){
if(root==null){
return null;
}
TreeNode leftNode = mirrorTree(root.left);
TreeNode rightNode = mirrorTree(root.right);
root.left=rightNode;
root.right=leftNode;
return root;
}
/**
* 求解二叉树的镜像(非递归方式)
* 思路:借助前序遍历的非递归方式改进
* @param root
*/
public void mirrorTreeLoop(TreeNode root){
if(root==null){
return;
}
Stack stack=new Stack();
stack.push(root);
while(!stack.isEmpty()){
TreeNode treeNode=(TreeNode)stack.pop();
//交换左右子树
TreeNode temp = treeNode.right;
treeNode.right=treeNode.left;
treeNode.left=temp;
if(treeNode.right!=null){
stack.push(treeNode.right);
}
if(treeNode.left!=null){
stack.push(treeNode.left);
}
}
}
/**
* 查找元素object所在的节点
* @param root
* @param object
* @return
*/
public TreeNode searchNode(TreeNode root,Object object){
if(root==null){
return null;
}
if(root.data.equals(object)){
return root;
}
TreeNode node = searchNode(root.left, object);
if(node==null){
node = searchNode(root.right, object);
}
return node;
}
public boolean isContains(TreeNode root,TreeNode node){
if(root==null){
return false;
}
if(root==node){
return true;
}
boolean isFound=false;
isFound=isContains(root.left, node);
if(!isFound){
isFound=isContains(root.right, node);
}
return isFound;
}
/**
* 二叉树的深度
* 递归解法:
* (1)如果二叉树为空,二叉树的深度为0
* (2)如果二叉树不为空,二叉树的深度 = max(左子树深度, 右子树深度) + 1
* @param root
* @return
*/
public int getTreeDepth(TreeNode root){
if(root==null){
return 0;
}
int leftDepth=getTreeDepth(root.left);
int rigthDepth=getTreeDepth(root.right);
int depth=leftDepth>=rigthDepth?leftDepth+1:rigthDepth+1;
return depth;
}
/**
* 获取二叉树的宽度
* 宽度的定义:二叉树每一层中节点的最多个数
* @param root
* @return
*/
public int getTreeWidth(TreeNode root){
if(root==null){
return 0;
}
int depth=getTreeDepth(root);
int width=0;
for(int i=1;i<=depth;i++){
int temp=getKthNodeNum(root, i);
if(temp>width){
width=temp;
}
}
return width;
}
/**
* 判断二叉树是不是完全二叉树(层次遍历)
* 定义:
* 若设二叉树的深度为h,除第 h 层外,
* 其它各层 (1~h-1) 的结点数都达到最大个数,
* 第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
* 算法判断:
* 按层次(从上到下,从左到右)遍历二叉树,
* 当遇到一个节点的左子树为空时,则该节点右子树必须为空,
* 且后面遍历的节点左右子树都必须为空,否则不是完全二叉树。
* @param root
* @return
*/
public boolean isCompleteBinaryTree(TreeNode root){
if (root==null) {
return false;
}
Queue queue = new LinkedBlockingQueue();
queue.add(root);
boolean flag=false;//判断是否出现了有左子树但无右子树的节点
while(!queue.isEmpty()){
TreeNode node = (TreeNode)queue.remove();
if(flag){//剩下的节点只能是叶子节点
if(node.left!=null||node.right!=null){//不是叶子节点的话,直接反回false
return false;
}
}else{
if(node.left!=null&&node.right!=null){
queue.add(node.left);
queue.add(node.right);
}else if(node.left!=null&&node.right==null){
queue.add(node.left);
flag=true;
}else if(node.left==null&&node.right!=null){
return false;//肯定不是完全二叉树
}else if(node.left==null&&node.right==null){
flag=true;
}
}
}
return true;
}
/**
* 获取根节点到任意节点node的路径(递归)
* 通过递归的方式,在左右子树上寻找,如果左右子树均没有,则删除该节点
* 否者,该节点是其路径上的节点之一
* @param root
* @param node
* @param list
*/
public boolean getTreePath(TreeNode root,TreeNode node,List list){
if(root==null){
return false;
}
list.add(root);
if(root==node){
return true;
}
boolean isFound=false;
isFound=getTreePath(root.left, node, list);//在左子树上寻找
if(!isFound){//如果左子树没找,在右子树上寻找
isFound=getTreePath(root.right, node, list);
}
if(!isFound){//左右子树都没有找到,说明这个节点没有,删除之,并返回false
list.remove(list.size()-1);
return false;
}
return true;
}
/**
* 寻找任意两个节点的最低公共祖先节点
* 思路:寻找根节点到node1的路径和到node2的路径
* 两条路径最后一个相同的节点即为最低公共祖先节点
* @param root
* @param node1
* @param node2
* @return
*/
public TreeNode getNearComParentNode(TreeNode root,TreeNode node1,TreeNode node2){
List path1=new LinkedList();
List path2=new LinkedList();
boolean flag1=getTreePath(root, node1, path1);
boolean flag2=getTreePath(root, node2, path2);
if(!flag1||!flag2){//其中有节点不在二叉树中
return null;
}
int i=0,j=0,index=0;
//搜索两条路径的最后一个相同的节点
while (i list= new ArrayList();
postOrderTraverse2(root, list);//后序遍历
int flag=0;
int i=0;
for(i=0;i1){
return false;
}
boolean isLeft=isAVLTree(root.left);
boolean isRight=isAVLTree(root.right);
return isLeft&&isRight;
}
/**
* 根据先序遍历和中序遍历重建二叉树
* 思路:递归
* 例如:先序遍历:ABDEFC 中序遍历:DBEFAC
* 1.先取出先序遍历的第一个节点,为根节点
* 2.根据根节点在中序遍历中的位置,将中序遍历分割成2部分
* 3.根据中序遍历分割后的长度,将先序遍历对应分割
* 4.递归方式,重建左子树和右子树
* @param perOrder
* @param inOrder
* @return
*/
public TreeNode rebuildTree(List perOrder,List inOrder){
if(perOrder.size()!=inOrder.size()){//参数有误
return null;
}
TreeNode root=null;
if(perOrder.size()>0){
root=new TreeNode();//新建节点
Object perRoot=perOrder.get(0);//前序遍历的第一个节点为根节点
root.data=perRoot;
int indexInOrder=inOrder.indexOf(perRoot);//查找根节点在中序节点的位置
//根据根节点的位置,接那个中序遍历分成左右两个中序序列
List leftInOrder=inOrder.subList(0,indexInOrder);
List rightInOrder=inOrder.subList(indexInOrder+1,inOrder.size());
//根据左右中序遍历的长度,依次分割其对应的前序遍历
List leftPerOrder=perOrder.subList(1, leftInOrder.size()+1);
List rightPerOrder=perOrder.subList(leftInOrder.size()+1,perOrder.size());
//递归的方式,依次重建
root.left=rebuildTree(leftPerOrder, leftInOrder);
root.right=rebuildTree(rightPerOrder, rightInOrder);
}
return root;
}
public void test(){
TreeNode root=new TreeNode();
root.data="A";
TreeNode nodeB=new TreeNode();
nodeB.data="B";
TreeNode nodeC=new TreeNode();
nodeC.data="C";
TreeNode nodeD=new TreeNode();
nodeD.data="D";
TreeNode nodeE=new TreeNode();
nodeE.data="E";
TreeNode nodeF=new TreeNode();
nodeF.data="F";
//////////////////////设置节点的关系
root.left=nodeB;
root.right=nodeC;
nodeB.left=nodeD;
nodeB.right=nodeE;
nodeE.right=nodeF;
///////////一下测试上述方法的正确性
List list = new LinkedList();
// preOrderTraverse(root, list);
// preOrderLoop(root,list);
// inOrderTraverse(root, list);
// inOrderLoop(root, list);
// postOrderTraverse(root, list);
// postOrderLoop(root, list);
// levelOrderTraverse(root, list);
// for(Object object:list){
// System.out.print((String)object+" ");
// }
// System.out.println(getKthNodeNum(root, 4));
// System.out.println(getLeafNodeNum(root));
// System.out.println(getNodeNum(root));
// TreeNode treeNode = searchNode(root, "E");
// System.out.println(treeNode.right.data);//F
// System.out.println(getTreeDepth(root));
// TreeNode newRootNode = mirrorTree(root);
// levelOrderTraverse(newRootNode, list);
// for(Object object:list){
// System.out.print((String)object+" ");
// }
// mirrorTreeLoop(root);
// levelOrderTraverse(root,list);
// for(Object object:list){
// System.out.print((String)object+" ");
// }
// System.out.println(isCompleteBinaryTree(root));
// getTreePath(root, nodeC, list);
// for(Object object:list){
// System.out.print((String)((TreeNode)object).data+" ");
// }
// TreeNode node= getNearComParentNode2(root, nodeE, nodeF);
// System.out.println(node.data);
// System.out.println(getTreeWidth(root));
// System.out.println(isAVLTree(root));
List perOrderList = new LinkedList();
List inOrderList = new LinkedList();
preOrderTraverse(root, perOrderList);
inOrderTraverse(root, inOrderList);
TreeNode treeNode=rebuildTree(perOrderList, inOrderList);
List postOrderList=new LinkedList();
postOrderTraverse(treeNode, postOrderList);
for (Object object : postOrderList) {
System.out.print((String) object + " ");
}
}
public static void main(String[] args) {
MyBinaryTree myBinaryTree = new MyBinaryTree();
myBinaryTree.test();
}
}
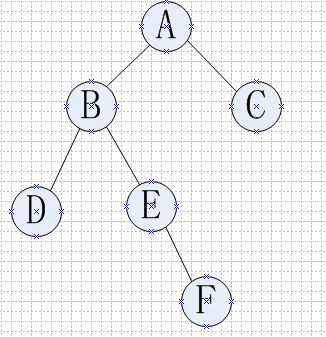
测试用例中所用的二叉树结构如下图: