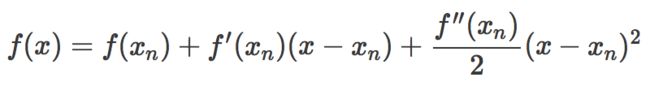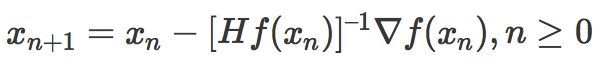深度学习之Hessian矩阵在牛顿法中的应用
对于多维函数,每个点在每一个方向上的导数是不同的,如果使用梯度下降,有可能在某一方向上导数增加很快,而在另外一方向上增加很慢,梯度下降是不知道导数的这些信息的,因为梯度只是一阶导数,只有二阶导数能反应一阶导数的变化情况,也就是Hessian矩阵。
一般来说, 牛顿法主要应用在两个方面, 1, 求方程的根; 2, 最优化.
1), 求解方程
并不是所有的方程都有求根公式, 或者求根公式很复杂, 导致求解困难. 利用牛顿法, 可以迭代求解.
原理是利用泰勒公式, 在x0处展开, 且展开到一阶, 即f(x) = f(x0) + (x-x0) f’(x0)
求解方程f(x) = 0, 即f(x0) + (x-x0)f'(x0) = 0, 求解x = x1 = x0 - f(x0)/f’(x0), 因为这是利用泰勒公式的一阶展开, f(x) = f(x0) + (x-x0) f’(x0)处并不是完全相等, 而是近似相等, 这里求得的x1并不能让f(x) = 0 ,只能说f(x1) 的值比f(x0) 更接近f(x) = 0, 于是乎, 迭代求解的想法就很自然了, 可以进而推出
Xn+1=Xn - f(Xn)/f’(Xn) 通过迭代, 这个式子必然在f(x*) = 0的时候收敛. 整个过程如下图:
![]()
2), 最优化
这次为了求解f' =0的根, 首先把f(x)在探索点Xn处泰勒展开, 展开到2阶形式进行近似:
然后用f(x)的最小点做为新的探索点Xn+1,据此,令:
求得出迭代公式:
一般认为牛顿法可以利用到曲线本身的信息, 比梯度下降法更容易收敛(迭代更少次数), 如下图是一个最小化一个目标方程的例子, 红色曲线是利用牛顿法迭代求解, 绿色曲线是利用梯度下降法求解.
![]()
在上面讨论的是2维情况, 高维情况的牛顿迭代公式是:
通过牛顿法迭代地更新近似函数和跳到近似函数的最小点可以比梯度下降更快地到达临界点,但是只有当附近的临界点时最小点(Hessian的所有特征值都是正的)时牛顿法才适用,因为它会被吸引到鞍点。
参考
http://jacoxu.com/jacobian矩阵和hessian矩阵/