Tightly Coupled LiDAR Inertial Odometry and Mapping源码解析(一)
Tightly Coupled LiDAR Inertial Odometry and Mapping源码解析(一)
- 1. LiDAR inertial odometry and mapping简介
- 2. Tightly coupled LiDAR inertial odometry
- 2.1 LiDAR-IMU odometry overview
- 2.2 IMU and pre-integration
- 2.3 De-skewing and feature extraction
- 2.4 Relative lidar measurements
1. LiDAR inertial odometry and mapping简介
在利用3D LiDAR进行SLAM计算时,有时会遇到一些问题,例如两帧之间的运动较为剧烈(大转角)可能会导致点云配准算法失效,在某些场景如长廊场景下有效测量点云较少使运动估计精度下降等,这些现象影响了SLAM算法的鲁棒性。而IMU(Inertial Measurement Unit)作为一种惯性测量单元,可以精确地测量载体的三轴加速度以及三轴角速度,在上述的场景中(大转角,长廊环境)可以为LiDAR提供额外的先验信息,从而增强LiDAR算法的鲁棒性,因此LiDAR-IMU fusioin成为一种近年来备受关注的SLAM方法。事实上,camera-IMU融合已经有一些开源的SLAM算法,例如VINS Mono。在ICRA 2019 上,终于迎来了第一个开源的LiDAR-IMU SLAM算法LIOM(Lidar-Inertial Odometry and mapping),由香港科技大学的刘明老师及学生共同完成,其主要贡献如下:
- 提出了一种紧耦合的LiDAR-IMU里程计算法,可实现实时、高精度以及高更新率(High update rate)的里程计计算
- 利用LiDAR-IMU里程计的先验信息,基于旋转约束的优化方法进一步优化位姿和点云地图,以生成全局一致、鲁邦的地图和位姿估计
- 进行了大量的室内外实验测试,实验结果优于LiDAR-only或LiDAR-IMU松耦合方法
- 第一个开源的LiDAR-IMU紧耦合SLAM算法(LIO-Mapping)
2. Tightly coupled LiDAR inertial odometry
2.1 LiDAR-IMU odometry overview
整个LiDAR-IMU里程计的算法流程如下图所示:
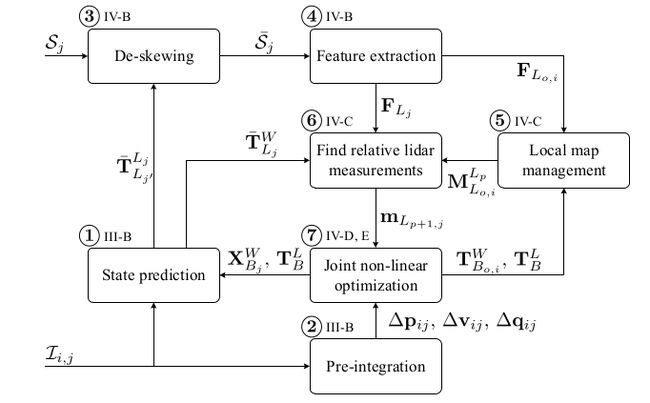
为了更好的理解LIO算法,我们一起看下面这幅时序图:

假设当前的时间戳是 i i i,则由于一般IMU设备的频率(100-1000Hz)会远远高于LiDAR点云数据的更新频率(10Hz),因此在下一帧点云即时间戳 j j j到来之前,会有大量的IMU数据 τ i , j \tau_{i,j} τi,j读入,如上图中紫色线条所示。则可以根据这段时间内IMU的数据对IMU的状态进行估计,即流程图中的state-prediction部分,同时利用这段时间间隔内的IMU测量量进行预积分操作,即对应流程图中的Pre-integration。当到达时间戳 j j j也即新的激光雷达数据帧过来后,由于激光雷达为连续测量,即在时间戳 i i i到时间戳 j j j过程中,激光雷达的测量是在不断运动且位姿不断变化的过程中测量得到的,因此会产生一定的运动畸变(motion distortion)。此时,在获得时间戳 j j j对应的激光点云数据 S j S_j Sj后,应首先根据IMU的state-prediction消除运动畸变即流程图中的De-skewing部分从而得到未畸变的点云 S ‾ j \overline{S}_j Sj。
在得到畸变矫正后的点云 S ‾ j \overline{S}_j Sj后,为减少计算量,采用了LOAM中的方法从点云提取了两种特征 F L j F_{L_j} FLj,分别是角点以及平面特征点,即对应流程图中的Feature Extraction部分。然后就是根据局部地图 M L o , i L p M_{L_{o,i}}^{L_p} MLo,iLp,确定特征与局部地图的对应关系,也即流程图中的Find relative lidar measurements部分。所谓的局部地图,也就是将上图所示的从时间戳 o o o到时间戳 i i i的特征点都投影到一个坐标系下形成一个点云局部地图,在本文中,每次都是投影到中间的时间戳即 p p p对应的坐标系下,即对应流程图中的Local map management。最后在确定了测量约束和IMU的预积分约束后,建立非线性最小二乘的目标函数并进行联合优化求解,即对应流程图中的Joint non-linear optimization部分。接下来,我们对LIO中的每一个子部分进行详细解析。
2.2 IMU and pre-integration
一般来讲,一个三轴正交的IMU设备可以测量三轴的加速度以及角速度,由牛顿运动定律,若初始状态(位置,姿态,速度)已知,则可以根据加速度以及角速度的测量跟踪一个物体的状态(位置,姿态,速度),因此广泛的应用于惯性导航(Inertial Navigation System)中。在涉及到IMU的导航系统中,通常IMU的状态可以建模为如下向量:
X B i W = [ p B i W T , v B i W T , q B i W T , b a i T , b ω i T ] T X_{B_i}^{W}=[{p_{B_i}^W}^T,{v_{B_i}^W}^T,{q_{B_i}^W}^T,b_{a_i}^T,b_{\omega_i}^T]^T XBiW=[pBiWT,vBiWT,qBiWT,baiT,bωiT]T
其中 p B i W T {p_{B_i}^W}^T pBiWT表示的是IMU在 i i i时刻在世界坐标系 W W W下的位置, v B i W T {v_{B_i}^W}^T vBiWT表示的是IMU在 i i i时刻在世界坐标系 W W W下的速度,而 q B i W T {q_{B_i}^W}^T qBiWT表示的是IMU在 i i i时刻在世界坐标系 W W W下的姿态(四元数),最后两个 b a i T , b ω i T b_{a_i}^T,b_{\omega_i}^T baiT,bωiT则是IMU原始测量数据即加速度以及角速度测量的偏置,可以理解为一种IMU原始测量数据的误差建模。在本文中,由于涉及到LiDAR-IMU融合,LiDAR与IMU之间为刚性链接且未先前标定,因此状态向量除了IMU状态向量 X B i W X_{B_i}^{W} XBiW外,还要估计LiDAR和IMU之间的相对位姿关系,即:
T B L = [ p B L , q B L ] T T_B^L=[p_B^L,q_B^L]^T TBL=[pBL,qBL]T
根据高中学过的牛顿运动定律 x = x 0 + v 0 t + 1 2 a t 2 , v = v 0 + a t x=x_0+v_0t+\frac{1}{2}at^2,v=v_0+at x=x0+v0t+21at2,v=v0+at,我们可以根据IMU的原始测量数据以及前一时刻 i i i,IMU的状态,对当前时刻 j j j,IMU的状态进行更新,即:
p B j W = p B i W + ∑ k = i j − 1 ( v k Δ t + 1 2 ( g W + R k ( a ^ k − b a k ) ) Δ t 2 ) v B j W = v B i W + ∑ k = i j − 1 ( g W + R k ( a ^ k − b a k ) ) Δ t q B j W = q B i W ∏ k = i j − 1 δ q k p_{B_j}^W=p_{B_i}^W+\sum_{k=i}^{j-1}(v_k\Delta t+\frac{1}{2}(g^W+R_k(\hat{a}_k-b_{a_k}))\Delta t^2)\\ v_{B_j}^W=v_{B_i}^W+\sum_{k=i}^{j-1}(g^W+R_k(\hat{a}_k-b_{a_k}))\Delta t\\ q_{B_j}^W=q_{B_i}^W\prod_{k=i}^{j-1}\delta q_k pBjW=pBiW+k=i∑j−1(vkΔt+21(gW+Rk(a^k−bak))Δt2)vBjW=vBiW+k=i∑j−1(gW+Rk(a^k−bak))ΔtqBjW=qBiWk=i∏j−1δqk
因此,时间戳 i i i到时间戳 j j j内IMU的运动可以利用预积分建模为:
z i , j = { Δ p i j , Δ v i j , Δ q i j } z_{i,j}=\{\Delta p_{ij},\Delta v_{ij},\Delta q_{ij}\} zi,j={Δpij,Δvij,Δqij}
2.3 De-skewing and feature extraction
这一部分主要实现点云畸变矫正以及从畸变矫正的点云中提取特征,主要借鉴了LOAM的畸变矫正以及特征提取方法,因此在这里仅简单描述一下畸变矫正以及特征提取的思路,细节还请阅读LOAM源码。
我们都知道,激光雷达的测量与摄像头的测量不太相同。摄像头的拍照可以理解为one-shot,即快门曝光的时刻。而激光雷达的测量则是连续测量,也即每一帧点云中的不同点其实都是在不同时刻测量得到的。而车载的激光雷达又都是在不断运动的,这就导致该帧点云中的每一个点其实都是在不同的时刻测量得到的。因此需要根据IMU的加速度以及角速度信息(插值等方法)预测每一个激光扫描点测量时,该点对应的激光雷达的位置。具体这部分具体实现也可以参考LOAM源码。
2.4 Relative lidar measurements
这部分非常有趣,刚看这篇论文时十分困惑,我去relative lidar measurements,以前没听过啊我靠,好高端,得好好研究研究,甚至去逐行看了源码(源码质量不错)。研究了一番后,发现其实也不过是为了给优化函数添加约束建立了一种特征点到局部地图的关联罢了,其实从这个角度看还是蛮好理解的。
如下图所示,这篇论文采用了滑动窗口(sliding window)的方法,图中B表示的是IMU坐标系,L表示的是激光雷达坐标系,在运动过程中假设两者之间的相对位姿关系不发生变化(刚性连接)。蓝色的大窗口即是论文中说的sliding window,在源码中该window设置为包含了15个激光雷达帧大小的窗口,其中从 o o o到 p p p为之前优化过的帧,而从 p p p到 i i i对应的帧为待优化的帧。
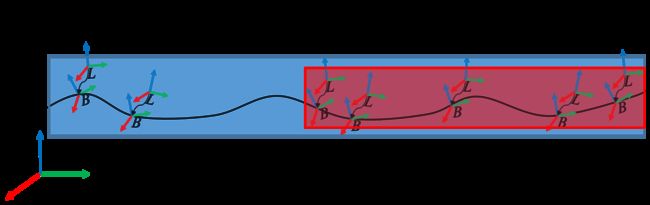
为了建立特征点到局部地图的关联关系,当然应该首先建立局部地图对吧。有的同学可能会问了,直接进行点云帧之间的关联不就可以了吗,这样不就是一个简答的激光里程计吗?问题在于啊,一帧的点云通常还是比较稀疏的,尤其是线数比较低的点云,建立稠密局部地图可以使得特征之间的匹配更为准确。现在假设我们根据2.3节中所述LOAM的特征提取方法,分别提取出来了每一帧的平面特征点,但是这些特征点都是定义在自己的局部激光雷达坐标系 O L i O_{L_i} OLi内的哦。因此为了建立坐标系统一的局部地图,我们首先应该要找一个基准,然后大家把自己的点云都投影到这个基准下面。在论文中,这个基准就是 p p p时刻对应的雷达坐标系 O L p O_{L_p} OLp。接下来的问题就是怎么投影了,其实就是一些简单的坐标变化关系,我们一起来看一下。
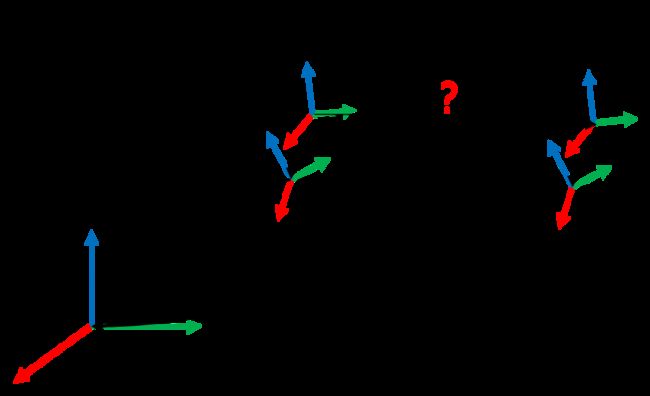
现在已知 i i i时刻和 p p p时刻IMU坐标系到世界坐标系的位姿变化关系即 T B i W T_{B_i}^{W} TBiW和 T B p W T_{B_p}^{W} TBpW,且已知激光雷达到IMU坐标系之间的变换关系 T L B T_L^B TLB(外参:待标定),则根据坐标变换的链式法则,可以得到 i i i时刻激光雷达坐标系到 p p p时刻激光雷达坐标系之间的变换关系为:
T L P = T L B T B i W T B p W − 1 T L B − 1 T_L^P=T_L^BT_{B_i}^W{T_{B_p}^W}^{-1}{T_L^B}^{-1} TLP=TLBTBiWTBpW−1TLB−1
在建立完局部地图(Local map)后,就要寻找特征到局部地图的对应关系了。对于待优化窗口(红色)内的某一帧,我们可以根据2.2节中IMU的预积分得到该帧的IMU位姿,然后就可以根据上式的坐标变换关系将该帧内的特征点 F l F_l Fl也投影到 p p p对应的激光雷达坐标系内。对于 F l F_l Fl内的每一个平面特征点,我们需要确定其与特征地图的对应关系。也就是说,如果所有测量都没有误差,由于局部地图是由平面特征点构成的,则 F l F_l Fl中的每一个特征点都应该落在局部地图的平面上。然而,实际情况是IMU和雷达的测量都会存在误差,导致预估的位姿不准确,同时激光雷达与IMU的相对位姿关系也存在误差,因此该特征点不是严格的落在局部地图的平面上。因此我们可以建立点到面的对应关系,首先在局部地图内搜索5个紧邻点,然后这5个近邻点可以拟合出一个平面,这样就可以用点到面的距离来作为约束啦。看起来比较简单,不过实现的时候还是有很多细节的,将在后面的源码博客中一一介绍,目前这篇博客先专注于LiDAR-IMU紧耦合的原理。
我们再回头看2.1节中的算法流程图,似乎只有联合优化(Joint non-linear optimization)没有讲了,考虑到这部分比较重要,且这篇博客篇幅有点长,将在下一篇博客中介绍。