树和二叉树

一、树的定义

  树是n(n>=0)个节点的有限集。当n=0时，称为空树。在任意一个非空树中，有如下特点：

《1》有且仅有一个特定的称为根的节点。

《2》当n>1时，其余节点可分为m(m>0)个互不相交的有限集，每一个集合本身又是一个树，并成为根的子树。

《3》树的最大层级数，被称为树的高度或深度。

二、二叉树

①二叉树是树的一种特殊形式【这种树的每个节点最多只有2个孩子节点】。

②二叉树的两个孩子节点被分别称为【左孩子、右孩子】。

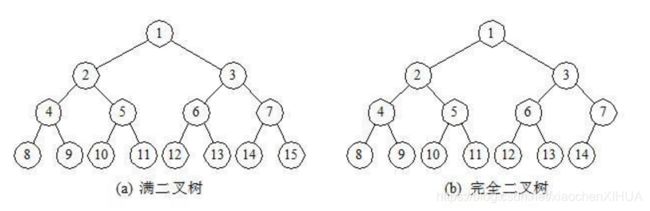
③二叉树还有两种形式【满二叉树、完全二叉树】。

《1》满二叉树：一个二叉树的所有非叶子节点都存在左右孩子，并且所有叶子节点都在同一层级上【要求所有的分支都是满的】

《2》完全二叉树：对于一个有n个节点的二叉树，按层级顺序编号，则所有节点的编号从1到n。且这个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同【只需要保证最后一个节点之前的节点都齐全即可】

三、二叉树的存储

  二叉树可以使用【链式存储结构、数组存储结构】

《1》链式存储结构：链表是一对一的存储方式，每一个链表节点都拥有data变量和一个指向下一个节点的next指针；而二叉树的一个节点最多可以指向左右两个孩子节点，所以每一个二叉树的每一个节点包含3个部分：

<1>存储数据的Data变量

<2>指向左孩子的left指针

<3>指向右孩子的right指针

《2》数组存储结构：使用数组结构存储时，会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子或右孩子空缺，则数组的相应位置也空出来了。

 <1>如果一个父节点的下标是[ParentIndex],那么它的左孩子节点下标就是[2*ParentIndex+1],右孩子节点下标是[2*ParentIndex+2];

<2>对于一个稀疏的二叉树来说，用数组表示法是非常浪费空间的。

四、二叉树的应用

二叉树包含许多的特殊形式，每种形式都有自己的作用，但是最主要的应用还是在进行【查找操作、维持相对秩序】这两方面。

《1》二叉查找树

二叉查找树在二叉树的基础上又增加了以下3个条件

<1>如果左子树不为空，则左子树上所有节点的值均小于根节点的值。

<2>如果右子树不为空，则右子树上所有节点的值均大于根节点的值。

<3>左右子树也都是二叉查找树。

《2》二叉树的遍历

  二叉树的遍历分为两大类【深度优先、广度优先】

<1>深度优先遍历：前序遍历（输出顺序：根节点、左子树、右子树）、中序遍历（输出顺序：左子树、根节点、右子树）、后序遍历（左子树、右子树、根节点）

<2>广度优先遍历：层序遍历

①前序遍历（输出顺序：根节点、左子树、右子树）

由根节点出发，如果跟节点存在左孩子，则输出左孩子，然后查看该输出的左孩子是否存在左孩子，如果存在则输出左孩子，否则输出右孩子，然后回退。

 

②中序遍历（输出顺序：左子树、根节点、右子树）

首先访问根节点的左孩子，如果左孩子还拥有左孩子，则继续深入访问下去，直到不再存在左孩子节点，并输出该节点；然后是输出该最后左孩子节点的根节点、根节点对应的右孩子，以此类推。

 

②后序遍历（输出顺序：左子树、右子树、根节点）

首先访问根节点的左孩子，如果左孩子还拥有左孩子，则继续深入访问下去，直到不再存在左孩子节点，并输出该节点；然后是输出该最后左孩子节点的右孩子、左孩子对应的跟节点，以此类推。

五、树核心

/***
*	Title:  "算法" 项目
*	主题 : 二叉树
*	Description: 
*	功能 : 
*	Date:  2020-07-05
*	Version:  1.2
*	Author:  Coffee
*	Modify Recoder:  
*/

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace Kernal
{
    class BinaryTree
    {
        //创建二叉树
        public static List CreateBinaryTree(LinkedList inputList)
        {
            List listTreeNode=new List();
            if (inputList==null && inputList.Count<=0)
            {
                return null;
            }

            foreach (var data in inputList)
            {
                TreeNode node = new TreeNode();
                node.data=data;
                node.leftNode =new TreeNode();
                node.rightNode = new TreeNode();

                listTreeNode.Add(node);
            }


            return listTreeNode;
        }

        //二叉树前序遍历
        public static void PreOderTraveral(TreeNode node)
        {
            if (node==null)
            {
                return;
            }
            Console.WriteLine(node.data);
            PreOderTraveral(node.leftNode);
            PreOderTraveral(node.rightNode);
        }

        //二叉树中序遍历
        public static void MidOderTraveral(TreeNode node)
        {
            if (node == null)
            {
                return;
            }
           
            MidOderTraveral(node.leftNode);
            Console.WriteLine(node.data);
            MidOderTraveral(node.rightNode);
        }

        //二叉树后序遍历
        public static void SufOderTraveral(TreeNode node)
        {
            if (node == null)
            {
                return;
            }

            SufOderTraveral(node.rightNode);
            SufOderTraveral(node.leftNode);
            Console.WriteLine(node.data);
            
        }


        //二叉树节点
        public class TreeNode
        {
            public TreeNode leftNode;
            public int data;
            public TreeNode rightNode;

        }

    }//Class_end
}

六、示例

using System;
using System.Collections.Generic;
using System.Diagnostics;
using System.Linq;
using System.Text;
using Kernal;

namespace CommonSort
{
    class Program
    {
        static void Main(string[] args)
        {
           
            LinkedList inputList=new LinkedList(
                new int[] {9,2,3,8,4,7}
                );
            List treeNodes = BinaryTree.CreateBinaryTree(inputList);

           
            Console.WriteLine("\n前序遍历");
            foreach (var treeNode in treeNodes)
            {
                BinaryTree.PreOderTraveral(treeNode);
            }


            Console.WriteLine("\n中序遍历");
            foreach (var treeNode in treeNodes)
            {
                BinaryTree.MidOderTraveral(treeNode);
            }
            

            Console.WriteLine("\n后序遍历");
            foreach (var treeNode in treeNodes)
            {
                BinaryTree.SufOderTraveral(treeNode);
            }

            Console.Read();
        }//Main_end



    }//Class_end
}

七、运行结果