1001.Tetrahedron
思路:可以叉积,余弦定理+1/2absin,海伦公式,计算得1/h^2=1/a^2+1/b^2+1/c^2,a为1-n,所以期望为3*(1+1/2^2+...+1/n^2)/n
typedef long long ll;
const int N=6e6+10;
const int mod=998244353;
#define int ll
int n,m,k;
int inv[N],f[N];
void get_inv(int n,int p){
inv[0]=inv[1]=1;
for (int i=2;i<=n;i++){
inv[i]=inv[p%i]*(p-p/i)%p;
}
}
signed main(){
int T;
get_inv(N-1,mod);
int t=0;
for (int i=1;i1002.Funny String
1003.Boring Game
模拟写的不太好
const int N=5e5+10;
int n,m,k,p;
int a[N],c[N],nx[N];
int b[210][2000];
void dfs(int k,int n){
if (n==p)return;
for (int i=0;i=1;j--){
b[j][i]=++be;
}
}
}
for (int i=n;i>=1;i--){
for (int j=1;j<=p;j++){
if (j&1)printf("%d ",a[b[i][j]*2]);
else printf("%d ",a[b[i][j]*2-1]);
}
for (int j=1;j<=p;j++){
if (j&1)printf("%d",a[b[i][j]*2-1]);
else printf("%d",a[b[i][j]*2]);
if (i!=1||j!=p)printf(" ");
}
}
puts("");
}
return 0;
}
1004.Expression
1005.Array Repairing
1006.Alice and Bob
1007.Tree
//写的也不太好
思路:树形dp,要考虑的情况挺多的,dp[i][0]记录子树无>k的度的最大权值和,dp[i][0]记录子树存在一个>k的度的最大权值和。
当前x子树<=k-1时,dp[x][0]为dp[i][0]的和,dp[x][1]为一个dp[i][1]和其他dp[i][0]
当前x子树>k-1时,dp[x][0]为前k-1大的dp[i][0]的和,dp[x][1]为全部dp[i][0]的和或k-2个dp[i][0]和一个dp[i][1]的最大和
另外,dfs每搜到一个点要处理两次以上操作,一次记录到dp内,代表这个点不是根,k=k-1,另一次不记录到dp内,代表这个点是根,k=k,更新ans=max(ans,处理出的不记录到dp内的答案)
typedef long long ll;
const int N=2e5+10;
#define int ll
typedef pair pii;
int n,m,k,p;
int dp[N][2];
int ans,rt;
vectorv[N];
void dfs(int x,int fa){
int cnt=0;
for (pii i:v[x]){
if (i.first==fa)continue;
dfs(i.first,x);
dp[i.first][0]+=i.second;
dp[i.first][1]+=i.second;
cnt++;
}
k--;
if (cnt>k){
priority_queue q;
int r=0;
for (pii i:v[x]){
if (i.first==fa)continue;
q.push({dp[i.first][0],i.first});
r+=dp[i.first][0];
}
dp[x][1]=max(dp[x][1],r);
int cnt1=0,mx=0,e=0;
while (!q.empty()){
cnt1++;
if (cnt1<=k)dp[x][0]+=q.top().first;
if (cnt1==k)e=q.top().first;
q.pop();
}
for (pii i:v[x]){
if (i.first==fa)continue;
q.push({dp[i.first][0],i.first});
}
cnt1=0;
while (!q.empty()){
cnt1++;
int t=q.top().second;
if (cnt1<=k){
mx=max(mx,dp[x][0]-dp[t][0]+dp[t][1]);
}
else{
mx=max(mx,dp[x][0]-e+dp[t][1]);
}
q.pop();
}
dp[x][1]=max(mx,dp[x][1]);
}
else{
int mx=0;
for (pii i:v[x]){
if (i.first==fa)continue;
dp[x][0]+=dp[i.first][0];
mx=max(mx,dp[i.first][1]-dp[i.first][0]);
}
dp[x][1]=max(dp[x][1],dp[x][0]+mx);
}
ans=max(dp[x][1],ans);
k++;
if (cnt>k){
priority_queue q;
for (pii i:v[x]){
if (i.first==fa)continue;
q.push({dp[i.first][0],i.first});
}
int cnt1=0,mx=0,e=0,u=0;
while (!q.empty()){
cnt1++;
if (cnt1<=k)u+=q.top().first;
if (cnt1==k)e=q.top().first;
q.pop();
}
for (pii i:v[x]){
if (i.first==fa)continue;
q.push({dp[i.first][0],i.first});
}
cnt1=0;
while (!q.empty()){
cnt1++;
int t=q.top().second;
if (cnt1<=k){
mx=max(mx,u-dp[t][0]+dp[t][1]);
}
else{
mx=max(mx,u-e+dp[t][1]);
}
q.pop();
}
ans=max(mx,ans);
}
else{
int mx=0,u=0;
for (pii i:v[x]){
if (i.first==fa)continue;
u+=dp[i.first][0];
mx=max(mx,dp[i.first][1]-dp[i.first][0]);
}
ans=max(ans,u+mx);
}
}
signed main(){
int T,x,y,z;
scanf("%lld",&T);
while (T--){
scanf("%lld%lld",&n,&k);
ans=0;
for (int i=0;i<=n;i++){
v[i].clear();dp[i][0]=dp[i][1]=0;
}
for (int i=1;i1){
dfs(1,-1);
printf("%lld\n",ans);
}
else if (k==0){
puts("0");
}
else if (k==1){
int mx=0;
for (int i=1;i<=n;i++){
int r=0;
for (pii j:v[i]){
r+=j.second;
}
mx=max(mx,r);
}
printf("%lld\n",mx);
}
}
return 0;
}
1008.Set2
思路:概率dp
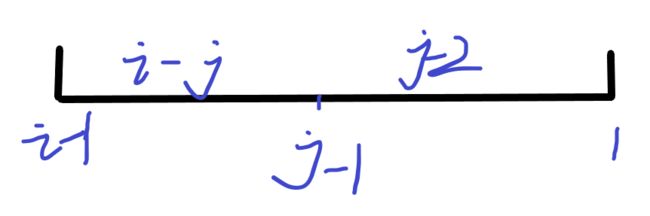
见代码理解图
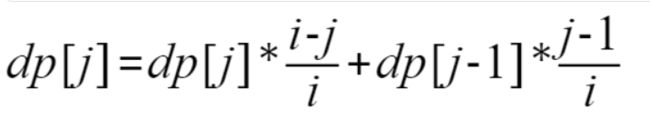
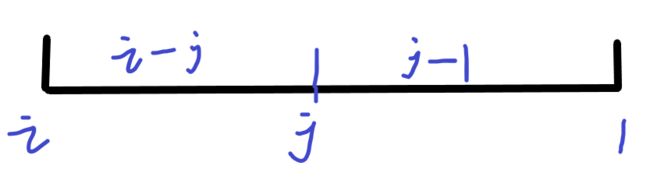
去除前面i-j个数中的一个可以变为
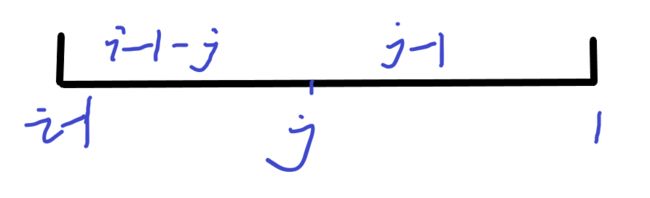
去除后面的j-1个数中的一个可以变为
typedef long long ll;
const int N=5e6+10;
const int mod=998244353;
#define int ll
int n,m,k;
int inv[N],dp[N];
void get_inv(int n,int p){
inv[0]=inv[1]=1;
for (int i=2;i<=n;i++){
inv[i]=inv[p%i]*(p-p/i)%p;
}
}
signed main(){
int T;
get_inv(N-1,mod);
scanf("%lld",&T);
while (T--){
scanf("%lld%lld",&n,&k);
int p=n%(k+1);
for (int i=0;i<=n;i++)dp[i]=1;//记录倒数第i个数能留下来的概率
for (int i=p+1;i<=n;i++){//当前还存在的数的数量,从最后只存在p个数的状态往前推
dp[i]=0;//新的数概率为0
if ((n-i)%(k+1)==0) continue;//这个数是第一个操作去除的
for (int j=i;j>=1;j--){
(dp[j]=dp[j]*(i-j)%mod*inv[i]%mod+dp[j-1]*(j-1)%mod*inv[i]%mod)%=mod;//如上图
}
}
for (int i=n;i>=1;i--){
if (i!=n)printf(" ");
printf("%lld",dp[i]);
}
puts("");
}
return 0;
}
1009.Paperfolding
思路:横着折x次,竖着折y次,剪开纸片数为(1+2^x)*(1+2^y)=2^(x+y)+2^x+2^y+1=2^n+1+2*(0Cn*2^0+...+nCn*2^n)/2^n=(二项式定理)2^n+1+2*3^n/2^n
typedef long long ll;
const int N=1e6+10;
const int mod=998244353;
#define int ll
int n,m,k;
int qpow(int x,int y){
int ans=1;
while (y){
if (y&1)ans=ans*x%mod;
y>>=1;x=x*x%mod;
}
return ans;
}
signed main(){
int T;
scanf("%lld",&T);
while (T--){
scanf("%lld",&n);
n%=mod-1;
int m=(qpow(3,n)*qpow(qpow(2,mod-2),n))%mod;
m=m*2%mod;
m=(qpow(2,n)+1+m)%mod;
printf("%lld\n",m);
}
return 0;
}
1010.Function
1011.Exam
1012.Set1
typedef long long ll;
const int N=5e6+10;
const int mod=998244353;
#define int ll
int n;
int inv[N],x[N],y[N],y2[N];
int cnt[N];
void get_inv(int n,int p){
inv[0]=inv[1]=1;
for (int i=2;i<=n;i++){
inv[i]=inv[p%i]*(p-p/i)%p;
}
}
int qpow(int x,int y){
int ans=1;
while (y){
if (y&1)ans=ans*x%mod;
y>>=1;x=x*x%mod;
}
return ans;
}
int C(int n,int m){
return x[n]*y[m]%mod*y[n-m]%mod;
}
signed main(){
int T;
get_inv(N-1,mod);
x[0]=y[0]=y2[0]=1;
for (int i=1;i1013.An Easy Matrix Problem