泊松图像编辑(Possion Image Edit)原理、实现与应用
虽然是2003年的文章了,但是由于其扎实的数学基础和至今看来都极其出色的效果,对每一个图像处理领域的学习者仍然是一篇值得一读的好文章。
本文同步发于Github.io,转载请注明来源
文章内容为参考论文原文与网络相关内容的个人理解,如有错误,请在评论区指出。
Poisson Image Editing - 2003
泊松图像编辑
有兴趣的朋友可以详细了解一下泊松方程的来历及其数学原理,在这里给几个可供参考的链接。
泊松方程的理论推导
从泊松方程的解法,聊到泊松图像融合
图像融合(1)Seamless cloning
我看网络上很多相关解读都是直接从泊松融合入手,其实这并不是泊松图像编辑的本质内容,只能算是一个非常惊艳的应用方法。泊松图像编辑的本质是修改图像的梯度,然后通过泊松方程解最优化问题,从新的梯度恢复出修改后的图像。其梯度的修改可以包括很多种:改变梯度来源(泊松融合)、对梯度频带截断(去纹理)、调整不同通道梯度比例(改变颜色)等等,文章将会对这些应用都有基础的介绍。
在这里,以论文提到的内容为准,对论文涉及的相关数学知识简单梳理一下。当然,对本部分实在没有兴趣的朋友可以跳过,只看后面也可以大致理解泊松编辑的原理和方法。
基于泊松方程的内插方法
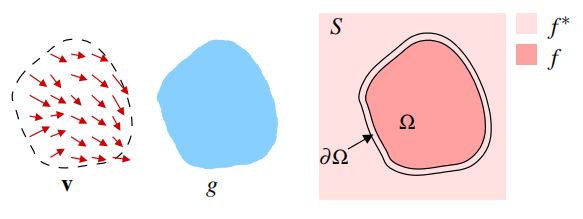
从上面两个图开始说起,假设左边的 S S S本来是一副好好的图片,那这时候我们在上面扣了一个洞,这个洞的样子大概就是右边这个图片,那这个 Ω \Omega Ω呢就表示这个洞的区域, ∂ Ω \partial\Omega ∂Ω则表示这个洞的边界。造成了这样的结果,是谁的错已经不重要了,总之我们现在想要把这个图像恢复要原来的样子,也就是想把这个洞填上。那现在没有任何可以参照的东西,剩下的只有带了洞的 S S S,唯一能够直接拿来用的也只有这个洞的边界像素值 ∂ Ω \partial\Omega ∂Ω我们还是知道的,想要填补这个洞,我们希望填出来的内容满足下面两个条件:
- 填补内容要尽可以平滑
- 填补内容的边界像素值和现有的 S S S一致,即要无缝过度
那要满足上述两个要求,就得到了以下的数学表达:
m i n f ∬ Ω ∣ ∇ f ∣ 2 with f ∣ ∂ Ω = f ∗ ∣ ∂ Ω (1) \underset{f}{min}\iint_{\Omega}\left|\nabla f\right|^2\ \text{ with }\ f|_{\partial\Omega}=f^*|_{\partial\Omega} \tag1 fmin∬Ω∣∇f∣2 with f∣∂Ω=f∗∣∂Ω(1)
其中 ∇ \nabla ∇是一阶微分,即梯度算子。那这个式子其实就是按照上面两个条件列出来的,意思就是在 Ω \Omega Ω区域梯度尽可能小(平滑),满足边界上像素相等的约束条件(无缝过度)。而上述最优化问题的解满足欧拉-拉格朗日方程:
Δ f = 0 over Ω with f ∣ ∂ Ω = f ∗ ∣ ∂ Ω (2) \Delta f=0\ \text{ over }\ \Omega \ \text{ with }\ f|_{\partial\Omega}=f^*|_{\partial\Omega} \tag2 Δf=0 over Ω with f∣∂Ω=f∗∣∂Ω(2)
其中 Δ \Delta Δ表示二阶微分(直角坐标系下的散度div),即拉普拉斯算子,也就是二阶梯度 ∇ 2 \nabla ^2 ∇2,学过图像处理的朋友应该很熟悉。而这个时候的边界条件就称为狄利克雷边界(Dirichlet boundary)。众所周知,取得一阶微分极值时,二阶微分等于0。所以要在梯度取最小的时候,就要在使得散度为0,因此就有了上式。已知区域 Ω \Omega Ω内的散度都是0,以及边界上已知的像素值,即可求出 Ω \Omega Ω内部所有像素值,根据以上方程填充的图像将会是以下结果。
上图从左到右分别为原图、填充区域、复原图。
看到这里想必有朋友已经怒拍键盘,看了半天你就给我糊一马赛克上去?
平心而论,有一说一,这个结果其实已经充分满足我们给出的条件了:1、填补内容尽可能平滑;2、颜色也在边界像素点的约束下与背景保持一致。
那之所以最后出现这样不堪入目的结果,是因为我们没有告诉它里面要填些啥东西,所以大家先坐下来继续看。这个时候我们就要稍微引导它一下,给它带入正规,这里就要用到引导向量场(guidance vector field), v \mathbf{v} v。
好了,上图多了 v \mathbf{v} v和 g \mathbf{g} g ,其中 v \mathbf{v} v是引导向量场,也就是梯度场,可以理解为从 g \mathbf{g} g中导出的。其实我们并不关心 g \mathbf{g} g是什么,我们只关心 v \mathbf{v} v是什么,它可以是从通过一张名为 g \mathbf{g} g的图中导出的,也可以是对原图 S S S中被扣掉的那部分里拿过来的,甚至可以是你随意生成的。不管它是怎么来的,总之现在我们又多了一个 v \mathbf{v} v,所以我们对填补任务又多出了新的要求:
- 填补内容的梯度要尽可以与 v \mathbf{v} v接近
- 填补内容的边界像素值和现有的 S S S一致,即要无缝过度
与式(1)和式(2)相对应的,现在我们得出了新的最优化问题:
m i n f ∬ Ω ∣ ∇ f − v ∣ 2 with f ∣ ∂ Ω = f ∗ ∣ ∂ Ω (3) \underset{f}{min}\iint_{\Omega}\left|\nabla f-\mathbf{v}\right|^2\ \text{ with } \ f|_{\partial\Omega}=f^*|_{\partial\Omega} \tag3 fmin∬Ω∣∇f−v∣2 with f∣∂Ω=f∗∣∂Ω(3)
同样的,该问题在狄利克雷边界约束下的泊松方程为:
Δ f = div v over Ω with f ∣ ∂ Ω = f ∗ ∣ ∂ Ω (4) \Delta f=\text{div}\mathbf{v}\ \text{ over }\ \Omega \ \text{ with } \ f|_{\partial\Omega}=f^*|_{\partial\Omega} \tag4 Δf=divv over Ω with f∣∂Ω=f∗∣∂Ω(4)
与之前相比,改变的仅仅是等式右边变成了由 v \mathbf{v} v计算的散度值而已。至于你选择用什么 v \mathbf{v} v,那就根据你的需求来了。在上述式子的基础上,同样的图像,再给出一个填充的实例。
上图从左到右分别为原图、填充区域、复原图。
—不是,整半天这和原图有什么区别?
—唉,好像左右镜像了一下。
—???
—卧槽?你少拿原图来骗我
不知道在看了结果以后,大家脑子里有没有这样的小剧场。在这里,我用的引导梯度 v \mathbf{v} v就是框选区域五边形内的 v \mathbf{v} v进行左右镜像后的 v \mathbf{v} v。由于本来就是从原图中选择的内容,边缘梯度变化和颜色值本来就非常接近,因此在经过泊松方程重建后几乎可以做到天衣无缝的图像编辑效果。
以上就是泊松图像编辑的核心内容。因为本人的数学功底比较一般,对几个方程并没有更加深入的剖析,也没有进行相关数学理论的推导,只是结合自己的理解进行了简单的分析。总之,对泊松图像编辑的总结就是:
- 本质:修改待插入区域的梯度
- 方法:解泊松方程
离散泊松方程解法
看了以上部分,应该多多少少对泊松图像编辑有了基本的认识,本部分将讲一讲离散泊松方程解法。
Δ f = div v over Ω with f ∣ ∂ Ω = f ∗ ∣ ∂ Ω \Delta f=\text{div}\mathbf{v}\ \text{ over }\ \Omega \ \text{ with }\ f|_{\partial\Omega}=f^*|_{\partial\Omega} Δf=divv over Ω with f∣∂Ω=f∗∣∂Ω
等式(4)就是泊松方程的核心了,在这里用一个简单的例子说明一下如何利用构建上述泊松方程。
以一个简单的 4 × 4 4\times4 4×4大小的图像进行说明,假设 X = [ x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14 x 15 x 16 ] X=\begin{bmatrix}x_1 & x_2 & x_3 & x_4 \\ x_5 & x_6 & x_7 & x_8 \\ x_9 & x_{10} & x_{11} & x_{12} \\ x_{13} & x_{14} & x_{15} & x_{16} \end{bmatrix} X=⎣⎢⎢⎡x1x5x9x13x2x6x10x14x3x7x11x15x4x8x12x16⎦⎥⎥⎤.
其中 x 6 , x 7 , x 10 , x 11 x_6,x_7,x_{10},x_{11} x6,x7,x10,x11四个点所构成的 2 × 2 2\times2 2×2大小的矩阵为我们所要填充的部分,像素值未知,但是散度已知(修改后的梯度所导出的散度)。其余位置为填充边界,像素值已知。因此只需要对上述4个待求点列出泊松方程即可:
{ x 2 + x 5 + x 7 + x 10 − 4 x 6 = div x 6 x 3 + x 6 + x 8 + x 11 − 4 x 7 = div x 7 x 6 + x 9 + x 11 + x 14 − 4 x 10 = div x 10 x 7 + x 10 + x 12 + x 15 − 4 x 11 = div x 11 \begin{cases}x_2+x_5+x_7+x_{10}-4x_6=\text{div}x_6 \\ x_3+x_6+x_8+x_{11}-4x_7=\text{div}x_7 \\ x_6+x_9+x_{11}+x_{14}-4x_{10}=\text{div}x_{10} \\ x_7+x_{10}+x_{12}+x_{15}-4x_{11}=\text{div}x_{11}\end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧x2+x5+x7+x10−4x6=divx6x3+x6+x8+x11−4x7=divx7x6+x9+x11+x14−4x10=divx10x7+x10+x12+x15−4x11=divx11
如上文所说,上述方程组中,右侧散度已知,左侧只有4个待求点函数值未知,4个方程刚好可以求解。
上述解法利用了待求区域周围一圈的像素值,即满足狄利克雷边界条件,值得一提的是,求解泊松方程还有一种约束条件,纽曼边界。
-
Neumann 边界,译为纽曼边界或黎曼边界,给出函数在边界处的二阶导数值
-
Dirichlet 边界,狄利克雷边界,给出边界处函数在边界处的实际值
不管怎么说,将上述求方程组的问题,用矩阵形式表示后即为 A x = B Ax=B Ax=B.
最后将求出来的 x x x代回图像中对应的位置即可。
Matlab实现
如果你只想直接调用函数测试,可以在python/C++直接使用OpenCV提供的接口。
如果你想研究一下代码及具体实现方式,那可以继续看一下这部分的内容。
我自己在用Matlab实现算法的时候,遇到了很多问题,例如出现边界过渡不自然等问题。简单的搜了一下度娘,关于详细实现部分居然很少,或者是代码不忍直视,也没去试效果。后来又在Github上找,找到的代码也不尽人意,于是还是自己动手,丰衣足食。
Matlab官网别人上传的代码
Github别人的repo
上面两个是我在编程过程中参考的代码,第一个代码在我个人实验的过程中发现其边界处理仍存在问题,第二个代码我借用了其UI界面部分的代码,用于选择融合区域并创建Mask。
我在尽可能保证代码能较好复现结果的前提下,增加了代码的可读性,并附上了比较详细的注释,有兴趣的朋友可以看看。代码包括接下来会讲到的各种应用的demo。
泊松图像编辑Matlab实现
应用
Seamless Cloning
这就是广为人知的泊松融合,有一副背景图像 S S S和另一幅源图像 g \mathbf{g} g,想要把 g \mathbf{g} g或 g \mathbf{g} g中的一部分插入到 S S S中,只需要用 g \mathbf{g} g的梯度作为引导梯度,解式(4)中的泊松方程即可。
此时的引导向量场 v = ∇ g \mathbf{v}=\nabla\mathbf{g} v=∇g。融合结果如下图所示:
看一下效果,嗯,一切都在计划之中。
但是,这是因为融合图像的背景都是水,看起来差不多,所以融合的结果也比较好。如果仔细看的话,还是能看到不少融合区域周围有一定的融合痕迹。而当你要融合两种背景纹理特征差异比较大的物体时,你就会发现出现问题了。以本文的标题图片为例:
背景木板上其实是有很多细节的,而我们截图的文字背景是非常平滑的单一颜色,因此引导梯度场可以说是基本都为0,最后导致了融合后的文字背景也非常平滑。那这样的结果显然不是我们期望的,我们希望既能将文字添加上去,又能保留木板上的纹理细节。论文中当然也提到了这部分,就是混合梯度融合。
Mixing Gradients Seamless Cloning
那要怎么做呢?还记得之前说的,图像编辑的本质是修改梯度。我们现在的做法是从一张图片中提取梯度,然后完全覆盖到背景图上去,现在我们想要保留两者中各自的高频细节,那相应的引导向量场就用两者较大的部分。

这一步需要先判断梯度的大小,然后取绝对值较大的梯度,然后根据新的梯度求取散度,再代入泊松方程求解,就可以得到以下结果。
OK,大功告成,这样看起来就舒服多了。当然,实际使用的时候还是要根据需求来,并不一定说混合梯度的效果绝对要比单一梯度效果好。如果有需求,甚至可以设计自适应加权的梯度修改方法。
Texture flattening
到了现在,大家应该都明白如何操作梯度来得到自己想要的结果了。那去纹理的意思显然就是把图像中的一部分纹理移除,同样的,在梯度修改时,我们直接放弃一部分梯度,所以对待求区域的每一个点作如下操作。
for all x ∈ Ω , v ( x ) = M ( x ) ∇ f ∗ ( x ) \text{for all} \ \mathbf{x} \in \Omega, \ \mathbf{v}(\mathbf{x})=M(\mathbf{x})\nabla f^*(\mathbf{x}) for all x∈Ω, v(x)=M(x)∇f∗(x),
其中 M ( x ) M(\mathbf{x}) M(x)是一个二值模板,即0-1,指示保留哪些梯度,删除哪些梯度。最简单的二值模板就是直接给一个阈值,只保留大于该阈值的信息或者小于该阈值的信息,下面给一个简单的例子:
grad(abs(grad)<0.08)=0;
emmmmm、抱歉、我的、打扰了、没控制好力度、重来、
grad(abs(grad)<0.02)=0;
嗯,大致效果就是这样,根据你截断的力度,会得到不同的编辑效果。直接用常数作阈值肯定是不合适的,更进一步也完全可以用自适应的方法选择保留哪部分的内容。
有点类似于边缘保持滤波器的效果,控制好力度或许能用来美颜这样?
Local illumination changes
可用于图像局部对比度提高或降低,类似于HDR的应用。
这里是对梯度域作了一个非线性变换,引用了以下这个论文,我也没仔细看,有兴趣的朋友可以自己去研究一下。Gradient Domain High Dynamic Range Compression
总之大致效果是这样的,还是很不错的:
Local color changes
用于改变图像局部颜色值,好处在于对改变目标不用框选很精确的区域,然后结果也比较自然。
方法很简单,就是对RGB三个通道的梯度值进行一定的增强和衰减,或者是替换等等各种操作,你喜欢怎么来就怎么来。直接给图:
左边原图
中间是论文给出的示例,梯度变化为:R*1.5,G/2,B/2
右边是我测试的结果,梯度变化为:R用B替换
效果1:
grad(:,:,1)=grad(:,:,1)*1.5;
grad(:,:,2)=grad(:,:,2)/2;
grad(:,:,3)=grad(:,:,3)/2;
效果2:
grad(:,:,1)=grad(:,:,3);
grad(:,:,2)=grad(:,:,2);
grad(:,:,3)=grad(:,:,3);
显然是右边的颜色比较好看,能否苟同?
Seamless tiling
论文给出的最后一个应用,对于一个矩形类内容的图像,类似补丁的一块,可以产生无缝拼接的效果。操作方法也很简单,修改图像的边界像素,就是第一行/列,最后一行/列。如:
row_1 = 0.5*(row_1+row_end);
row_end = row_1;
col_1 = 0.5*(col_1+col_end);
col_end = col_1;
即上下边界和左右边界设为原图像的边界和的一半。
然后引导向量场仍然使用原图像的梯度场。这样得到的结果就可以用来无缝拼接,如下图所示:
以上分别为直接拼接和泊松拼接的效果,看起来还是不错的。
总结
不提了,都在上面了。
参考
[1]Poisson Image Editing - 2003
[2]网络相关内容已在文中给出链接
[3]示例图片均来源于论文,木板背景来源百度图片,侵删