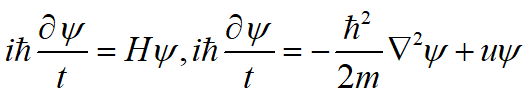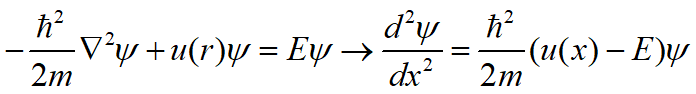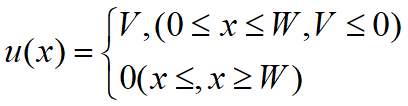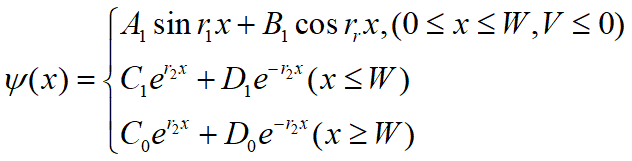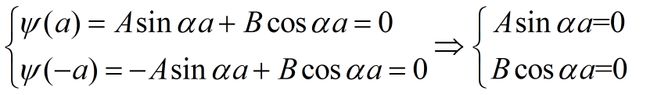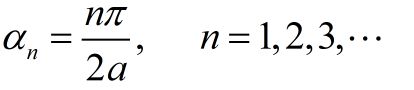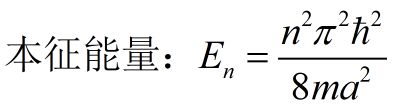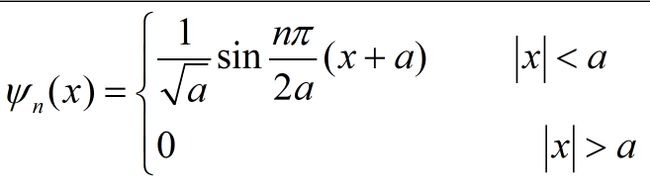一维方势阱中粒子能级和波函数matlab求解（定态薛定谔方程数值求解）

 

1.定态薛定谔方程

   薛定谔方程为量子力学中的基本方程，其揭示微观世界物质运动基本规律、是原子物理学中处理一切非相对论问题的有力工具。本文利用基础计算机数值模拟方法对其能级、波函数等性质求解。

   薛定谔方程通常表示：

                                                     

   若求能级与波函数，势函数不含时间，则代入下述方程： 

                                                    

   得到定态不含时的薛定谔方程：

                                                  

   2.一维方势阱中粒子能级、波函数模拟求解

                                                       

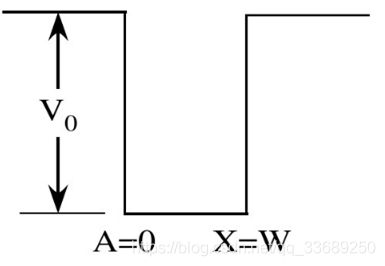
      对于如图一维方势阱问题，其势函数为：

                                                        

       带入上述微分方程，其解为：

                                                   

      利用边界条件确定系数A,B,C,D

     利用波函数连续性可得：

 

                                             

      求得：

                                                    

 

     经过推导得到归一化的本征函数：

                                                              

      3.matlab数值计算

     其计算流程图如下：

                                       

N=0;
V0=-20;
W=1.0;%势阱宽度
Emin=V0%势能
Emax=0;
M=51;%离散步长
de=(Emax-Emin)./(M-1);
E=Emin-de;
Ans=[];
for i=1:M-1
    E=E+de;
    r1=sqrt(abs(E-V0));
    r2=sqrt(abs(E));
    phi=(r2./r1)*sin(W*r1)+cos(W*r1);
    phi1=(r2*cos(W*r1)-r1*sin(W*r1));
    C1=0.5*(exp(-W*r2))*(phi+(phi1./r2));
    D1=0.5*(exp(W*r2))*(phi-(phi1./r2));
    N=floor((W*r1)./3.1415926);
    if (N-floor(0.5*N)*2~=0&&phi>0)
        N=N+1;
    end
    if (N-floor(0.5*N)*2==0&&phi<0)
        N=N+1;
    end
    if C1*D1<0
        if ((log(-D1./C1))./(2*r2))>W
            N=N+1;
            Ans(i,1)=E;
            Ans(i,2)=N;
        else
            Ans(i,1)=E;
            Ans(i,2)=N;
        end
    else
        Ans(i,1)=E;
        Ans(i,2)=N;
    end
end
count=2;
n=[0];%N值量子数
E=[Emin];
for i=1:size(Ans(:,2),1)
    if Ans(i,2)~=n(count-1)
        n(count)=Ans(i,2);
        E(count)=Ans(i,1);
        count=count+1;
    end
end
plot(n,E,'ro');
%ylim([-3,3]);
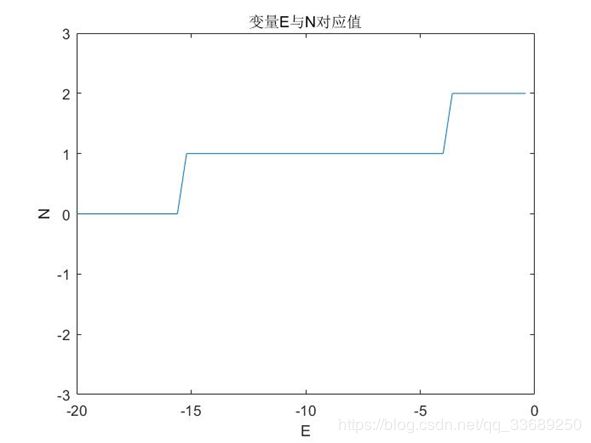
title('E与n对应值');
xlabel('n')
ylabel('E')

计算结果如下：

                           

                                                                            表 变量E与N对应值

1

E	-20	…	-15.6	-15.2	-14.8	…	-4.0	-3.6	…	-0.4
N	0	…	0	1	1	…	1	2	…	2

 

波函数绘图

 

 

L1=5;
x=0:0.01:L1;%势阱宽度
z1=(sqrt(2./L1))*sin((1*pi*x)./L1);
z2=(sqrt(2./L1))*sin((2*pi*x)./L1);
z3=(sqrt(2./L1))*sin((3*pi*x)./L1);
subplot(3,2,1);
plot(x,z1.^2);
%hold onlegend('n=1','n=2','n=3')
legend('n=1')
title('波函数');
xlabel('势阱宽度')
ylabel('概率密度')

%hold onlegend('n=1','n=2','n=3')
%%%%%%%%%%%%
subplot(3,2,2);
plot(x,z1);

legend('n=1')
title('波函数');
xlabel('势阱宽度')
ylabel('|波函数|')

%%%%%%%%%%%%%%%%%%%%%%%
subplot(3,2,3);
plot(x,z2.^2);
legend('n=2')
title('波函数');
xlabel('势阱宽度')
ylabel('概率密度')
subplot(3,2,4);
plot(x,z2.^2);
legend('n=2')
title('波函数');
xlabel('势阱宽度')
ylabel('概率密度')
%%%%%%%%%%%%%
%hold on
subplot(3,2,5);
plot(x,z3.^2);
legend('n=3')
title('波函数');
xlabel('势阱宽度')
ylabel('概率密度')
subplot(3,2,6);
plot(x,z3.^2);
legend('n=3')
title('波函数');
xlabel('势阱宽度')
ylabel('|波函数')
%set(gca,'ytick',[],'ycolor','w')