解析器模式实现简单四则运算
背景
在项目实施过程中,遇到客户提出一个需求:用户运用现有数学符号实现自定义公式,实现在线编辑公式,由系统实现解析。初次遇到这个需求,最初通过surfing找到一些优秀的开源算法包,例如Expression4J、MESP、Jep ,由这些工具包来负责解析字符串格式的算法公式。后来在学习过程中发现解析器模式可以用来描述这一类问题,并用解析器模式可以实现简单的四则运算,更复杂的算法过程应该也可以做,后续完善。
解析器模式
解释器模式是一种使用频率相对较低但学习难度较大的设计模式,它用于描述如何使用面向对象语言构成一个简单的语言解释器。在某些情况下,为了更好地描述某一些特定类型的问题,我们可以创建一种新的语言,这种语言拥有自己的表达式和结构,即文法规则,这些问题的实例将对应为该语言中的句子。此时,可以使用解释器模式来设计这种新的语言。对解释器模式的学习能够加深我们对面向对象思想的理解,并且掌握编程语言中文法规则的解释过程。
解释器模式定义如下:
由于表达式可分为终结符表达式和非终结符表达式,因此解释器模式的结构与组合模式的结构有些类似,但在解释器模式中包含更多的组成元素
其基础类图如下:
在解释器模式结构图中包含如下几个角色:
● AbstractExpression(抽象表达式):在抽象表达式中声明了抽象的解释操作,它是所有终结符表达式和非终结符表达式的公共父类。
● TerminalExpression(终结符表达式):终结符表达式是抽象表达式的子类,它实现了与文法中的终结符相关联的解释操作,在句子中的每一个终结符都是该类的一个实例。通常在一个解释器模式中只有少数几个终结符表达式类,它们的实例可以通过非终结符表达式组成较为复杂的句子。
● NonterminalExpression(非终结符表达式):非终结符表达式也是抽象表达式的子类,它实现了文法中非终结符的解释操作,由于在非终结符表达式中可以包含终结符表达式,也可以继续包含非终结符表达式,因此其解释操作一般通过递归的方式来完成。
● Context(环境类):环境类又称为上下文类,它用于存储解释器之外的一些全局信息,通常它临时存储了需要解释的语句。
各个类典型代码如下:
抽象表达式:
abstract class AbstractExpression {
public abstract void interpret(Context ctx);
} 终结符表达式:
class TerminalExpression extends AbstractExpression {
public void interpret(Context ctx) {
//终结符表达式的解释操作
}
} 非终结符表达式通常较为复杂,两个操作数的典型代码如下:
class NonterminalExpression extends AbstractExpression {
private AbstractExpression left;
private AbstractExpression right;
public NonterminalExpression(AbstractExpression left,AbstractExpression right) {
this.left=left;
this.right=right;
}
public void interpret(Context ctx) {
}
} Context类:
class Context {
private HashMap map = new HashMap();
public void assign(String key, String value) {
//往环境类中设值
}
public String lookup(String key) {
//获取存储在环境类中的值
}
} 对于一个简单的加减法解释器来说,例如:1+2+3-4-1。如何用文法来表示这么一个句子,每一个表达式都是由左表达式、操作符、右表达式来组合成的。可以使用下面的文法来解释这一类算法:
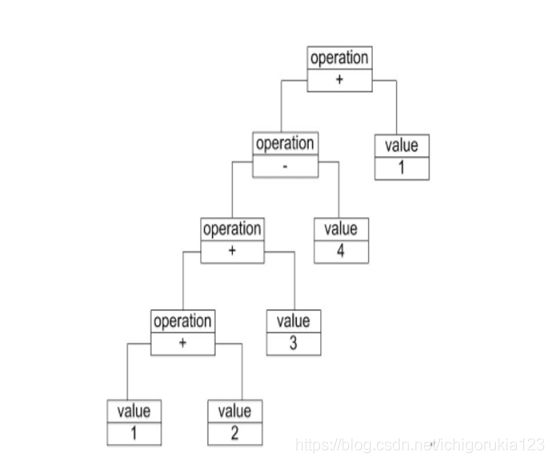
解析器模式还可以用如下的抽象语法树(Abstract Syntax Tree, AST)来表示算法:
在该抽象语法树中,可以通过终结符表达式value和非终结符表达式operation组成复杂的语句,每个文法规则的语言实例都可以表示为一个抽象语法树,即每一条具体的语句都可以用类似图22-2所示的抽象语法树来表示,在图中终结符表达式类的实例作为树的叶子节点,而非终结符表达式类的实例作为非叶子节点,它们可以将终结符表达式类的实例以及包含终结符和非终结符实例的子表达式作为其子节点。抽象语法树描述了如何构成一个复杂的句子,通过对抽象语法树的分析,可以识别出语言中的终结符类和非终结符类。
应用
了解了这种模式以后运用该设计模式来设计一个加减乘除运算解释器。
定义一个抽象表达式:
我的四则运算中终结符表达式只有一类,及数值型表达式:
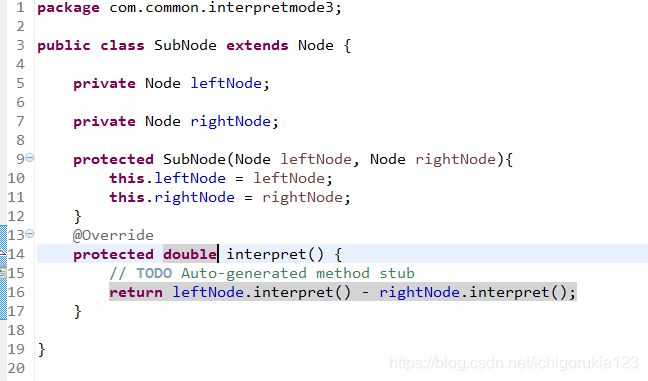
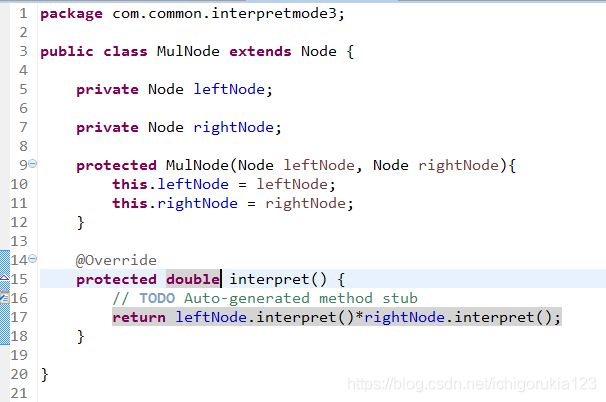
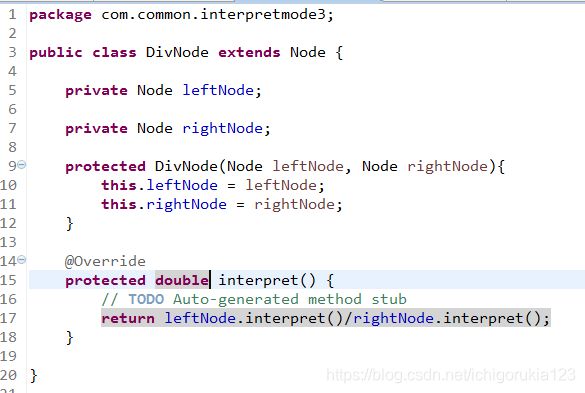
非终结符表达式有四类,加减乘除,分别为:
考虑到在四则运算中运算的优先级不同,乘除法优先于加减法进行计算。故规定优先级为除>乘>减>加。
环境类代码中运算优先级体现为:
环境类初始化时将优先级设置进来使用。
下一步解析原始字符串,并最终生成一个表达式,解析,过程简述如下:
Context中存两个栈,一个操作数栈,一个操作符栈,操作符入栈规则,
- 当操作符栈为空,直接入栈。
- 操作符栈不为空,如果当前操作符优先级大于栈顶操作符优先级,入栈;如果小于则pop出栈顶操作符并且pop操作数栈中两个数运算,将计算后的操作数压入操作数栈,同时继续判断当前操作符和操作符栈顶元素优先级,此处采用递归方式。常规的计算是直接进行数值的操作,而此处运用解析器模式压入操作数栈的实际上是运算表达式,当生成最后的表达式时,再来计算这个复杂的表达式的值。
package com.common.interpretmode3;
import java.util.HashMap;
import java.util.Map;
import java.util.Stack;
public class Context {
private String context;
private Node expression;
public void setExpression(Node expression) {
this.expression = expression;
}
Stack stack = new Stack();
Stack operation = new Stack();
private Map level = new HashMap();
public Context(String context,Map level){
this.context = context;
this.level = level;
}
/**
* 通过解析原始算法字符串,决定操作符栈中运算符优先级
*/
public void analysis(){
char[] origin = context.toCharArray();
for (int i = 0; i < origin.length; i++) {
if(origin[i]!='+' && origin[i]!='-'&&origin[i]!='*'&&origin[i]!='/'){
stack.push(new ValueNode(String.valueOf(origin[i])));
}else{
if(operation.empty()){
operation.push(String.valueOf(origin[i]));
}else{
combine(String.valueOf(origin[i]));
}
}
}
}
/**
* 判断操作符优先级
* @param left 操作符
* @param right 操作符
* @return
*/
private boolean compare(String left, String right){
return level.get(left) > level.get(right);
}
/**
* 递归判断新加入操作符栈中新加入的操作符应该处于的位置,保证优先级高的操作符位于栈顶
* @param curopt
*/
private void combine(String curopt){
if(compare(curopt,operation.peek())){
operation.push(curopt);
}else {
Node right = stack.pop();
Node left = stack.pop();
switch (operation.pop()) {
case "*":
stack.push(new MulNode(left, right));
break;
case "/":
stack.push(new DivNode(left, right));
break;
case "-":
stack.push(new SubNode(left, right));
break;
default:
stack.push(new AddNode(left, right));
break;
}
combine(curopt);
}
}
/**
* 分别取出操作符栈中操作符,和数值栈中的两个操作数进行组合计算,最终得到唯一的结果
* @return
*/
public Node getExpression(){
while(!operation.empty()){
switch (operation.pop()) {
case "/":
Node right = stack.pop();
Node left = stack.pop();
expression = new DivNode(left, right);
stack.push(expression);
break;
case "*":
expression = new MulNode(stack.pop(), stack.pop());
stack.push(expression);
break;
case "-":
Node rightNode = stack.pop();
Node leftNode = stack.pop();
expression = new SubNode(leftNode, rightNode);
stack.push(expression);
break;
default:
expression = new AddNode(stack.pop(), stack.pop());
stack.push(expression);
break;
}
}
return stack.peek();
}
public void execute(){
analysis();
expression = getExpression();
}
}
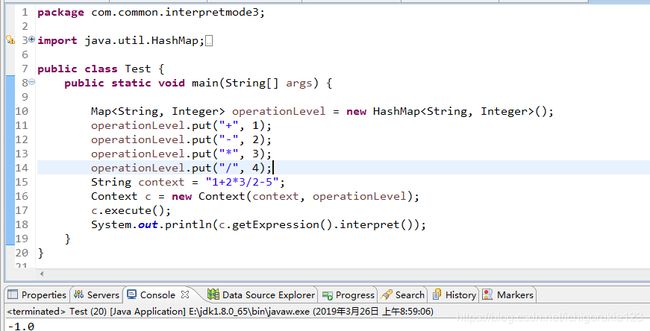
测试结果如下:
总结
运用解释器模式的优劣,
1. 主要优点
解释器模式的主要优点如下:
(1) 易于改变和扩展文法。由于在解释器模式中使用类来表示语言的文法规则,因此可以通过继承等机制来改变或扩展文法。
(2) 每一条文法规则都可以表示为一个类,因此可以方便地实现一个简单的语言。
(3) 实现文法较为容易。在抽象语法树中每一个表达式节点类的实现方式都是相似的,这些类的代码编写都不会特别复杂,还可以通过一些工具自动生成节点类代码。
(4) 增加新的解释表达式较为方便。如果用户需要增加新的解释表达式只需要对应增加一个新的终结符表达式或非终结符表达式类,原有表达式类代码无须修改,符合“开闭原则”。
2. 主要缺点
解释器模式的主要缺点如下:
(1) 对于复杂文法难以维护。在解释器模式中,每一条规则至少需要定义一个类,因此如果一个语言包含太多文法规则,类的个数将会急剧增加,导致系统难以管理和维护,此时可以考虑使用语法分析程序等方式来取代解释器模式。
(2) 执行效率较低。由于在解释器模式中使用了大量的循环和递归调用,因此在解释较为复杂的句子时其速度很慢,而且代码的调试过程也比较麻烦。