第三十五周学习笔记

第三十五周学习笔记

SuperPoint复现进度

code

detector可视化

Encoder架构

为了显示全图，省略了relu操作，relu就是stride为2，kernel_size为2的常规非线性操作，在每层卷积层后都有

Detector Head架构

输出是一个(15,20,65)的tensor，除去最后一维“no interest dustbin”之后，剩余的(15,20,64)的结果可以reshape成原图的大小(120,160)
Detector Head对Encoder得到的feature进行decode，通过增加深度，最后将深度重新reshape到长宽维上实现与原图一样大小的输出，这里之所以不使用upconvolution的原因是add a high amount of computation and can introduce unwanted checkerboard artifacts[18]

detector 的 Ground Truth 和 Label的关系

观察损失函数
$$L_p(X,Y)=\frac{1}{H_c{W}_c}\sum _{h=1,w=1}^{H_c,W_c}{l}_p({\mathbf{x}}_{hw};y_{hw})$$
其中，$H_c=H/8,W_c=W/8$，且
$$l_p({\mathbf{x}}_{hw};y)=-\log \frac{\exp ({\mathbf{x}}_{hwy})}{{\sum }_{k=1}^{65}\exp ({\mathbf{x}}_{hwk})}$$
注意到detector的输出是(15,20,65)的，除去最后一个深度维后，剩下(15,20,64)对应着原图（120,160）的15*24个8*8的区域，对每个这样的区域，关键点所在的第几个位置（将8/*8的区域拉成64维向量）即是$y_{hw}$的值，若区域中没有关键点，则$y_{hw}=65$，显然，从上面的损失函数中，默认了每个8*8区域中只有一个关键点，如果某个区域中有多于1个的关键点，则会在其中随机选择一个，虽然网络训练时使用随机的关键点，但是，实际的时候，大于最低置信度的点都会被认为是关键点，在训练过程中，只要多个关键点都多次被选中，可能可以检测出所有关键点。

样本不均衡问题

实际的标签上大多数是64（代表没有兴趣点），并没有特别的解决样本不均衡问题的方法，作者在pretrained model中设置了检测最低置信度为0.015（约为1/65），而tf实现中，检测的最低置信度更是0.001

网络debug

由于实际训练时，用上述的置信度，得出的网络输出的兴趣点都分布在如图的边缘，所以可能需要debug网络

使用单张图片放入网络训练

1.训练出的网络对输入不敏感，且输出的热力图的8*8网格中每个小格子输出一样


几乎差不多的热力图，网络的输出损失也很大，预测结果和全部热力图如下图，这是欠拟合的表现

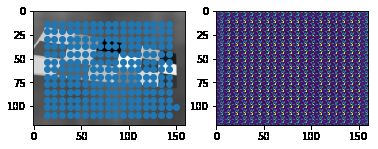
2.增大训练轮次后输出scale不同
损失小于1e-5，但预测时出现指数溢出，查看输出，发现15*20的每个65维输出的scale不一样，有的是0~80，有的是-40~0，统计结果如下

位于output[1,:,:]的统计结果

位于output[59,:,:]的统计结果

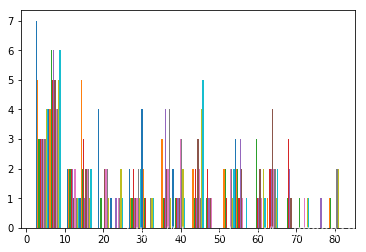
所以求exp的时候会溢出，loss的数值也不稳定，此时对每个15*20的channel求argmax时，得到的结果已经和label完全一致，可能是因为过拟合太多的原因，且在训练过程中，loss瞬间从0.5下降到0.002，可能是momentum在同一张图片上训练更新向量累积模太大，所以去掉momentum，且为防止过拟合，设定最小loss阈值

注意因为此处的输出求argmax后已经与label完全一样，我曾想通过归一化来保证预测时exp的数值稳定，但实际上是不可行的，因为不能做统一的归一化，这样会导致scale相对小的激活值输出的置信度很低，也不能做15*20区域中每个64维向量分别的归一化（？但是softmax的时候实际上是这样做的），这样会导致每个区域都有较大的激活值，问题是softmax在求损失函数的时候为什么数值是稳定的呢？

• 可能是因为输入没处理好的原因
• 可能是标签没处理好的原因
• 可能是输出转化到标签没处理好的原因
• 可能是loss函数不对的原因，计算了下损失的上界，-log(1/65) = 4.1744，与每次训练开始的误差是一致的
• 框之间的大小不可比？？？尽管是框中最大的激活值，还没有别的框中的非关键点激活值大？

3.在验证集上训练误差停在0.2左右下不去，且预测结果很差
考虑之后使用可变的学习率来改正

Pytorch MNIST分类

代码在这
本实验主要是使用Pytorch进行MNIST分类，并与pytorch-example的代码进行对比

pipline

• 下载并载入数据，本次只使用训练集1000，测试集200
• 浏览数据集
• 定义网络，全连接和卷积两种
  • 全连接网络：28*28->28*28->10，参数共计28*28*28*28+28*28*10=622496个
  • CNN：卷积核3*3，padding=1，stride=1，conv(1,8)->relu->pool->conv(8,16)->relu->fc，参数共计(3*3)*8+(3*3*8)*16+7*7*16*10=9064个
• 写出预测的代码，并用初始化的网络预测几个结果
• 调参，使用不同的学习率和momentum
• 训练
• 测试

结果分析

全连接

momentum=0

可见学习率对训练的影响，太小则太慢，太大则无法收敛

momentum=0.9

在有动量的情况下，加快了小学习率的优化速度，稍大的学习率在无动量情况下表现良好，但此时也会出现震荡

momentum VS no momentum

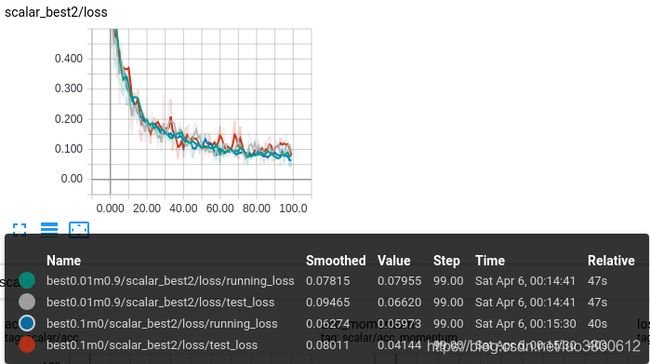
没有动量的方法稍微好一点，两者表现相差不大，但有动量因为额外的计算需要更长的时间

CNN

所有的参数中，表现好的参数有

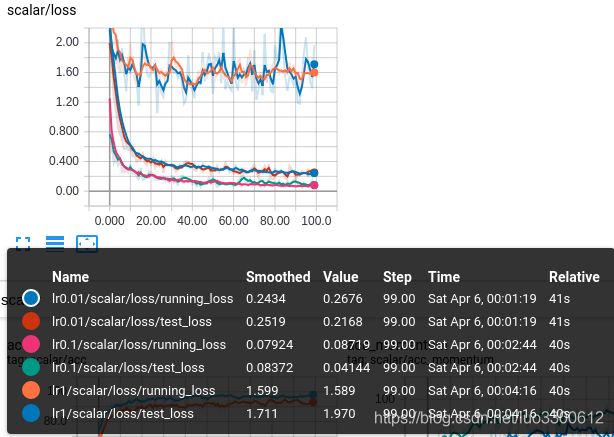
• lr=0.1，train_loss=0.0533，test_loss=0.1158
• lr=0.01，train_loss=0.0978，test_loss=0.0816
• lr=0.01，momentum=0.9，train_loss=0.06866，test_loss=0.06981

与之前的结果相似，小的学习率配上动量可以得到较好的结果，在这里大的学习率收敛快，因为没有正则化而出现了过拟合，本例使用的两个模型，在准确率上，CNN和全连接相差不大，但全连接的参数是CNN的68倍多

问题

对MNIST做或不做除以255有什么影响

原数据就是0~1之间的浮点数，不需要再除以255

使用或不使用momentum有什么影响

小学习率和momentum是好的组合

SGD with momentum的公式是啥

原来的公式是

x += learning_rate * gradient

加上momentum公式是

v = momentum * v - learning_rate * gradient
x += v

net在什么时候初始化参数？net.train还是什么？

网络在init方法后会自动初始化参数，net.train与net.eval是对特殊层（如bn、dropout）在训练和测试时切换表现的选项

tensor.data和tensor.item有啥区别

tensor.data虽然可以使用，但是文档中查不到，且返回还是一个tensor，而tensor.item()则返回python类型的数值，要求tensor是一个一维张量

输入图片的tensor是uint8还是float有啥区别

不知道

论文阅读 《Deep Residual Learning for Image Recognition》

概括

文章提出了深度残差学习网络，解决了深层网络难以优化的问题，核心思想是以学习残差代替学习直接映射，理论上这降低了网络学习到恒等映射的难度，从而使得更深的网络起码和浅的网络效果一样好

文章解决了什么问题

• 更深的神经网络更难训练，容易出现梯度爆炸和消失的问题，但初始化的正规化和中间层的正规化很大程度的降低了这一可能（不是本文主要解决的问题）
• 更深的网络的准确率达到饱和，进而不断下降，增加更多层反而引起更多的误差
• 这意味着这个系统难以优化（本文主要解决的就是更深的网络的优化问题）

用了什么方法

主要思想

理论上来说，更深的网络至少可以表现地和浅层的网络一样好，只要在一个浅层的网络加后加多层恒等变换层

提出了残差学习网络来降低深层神经网络的学习难度，网络不直接学习输入到输出的映射$H(x)$而学习输出和输入之差$F(x)=H(x)-x$，然后通过$F(x)+x$重建原映射，作者认为，如果恒等映射是最优的，这样的网络学习恒等变换比原来要简单（只要层的所有参数为0即可）

细节

x的传播可以很容易地使用shortcut connections实现

图中给出了ResNet的building block，定义为
$$y=F(x,\{W_i\})+x$$
其中$x$，$y$分别为输入和输出，$F$表示待学习的残差映射，比如在上图中，就有$F=W_2\sigma (W_{1}x)$，其中$\sigma$是ReLU函数，且为了简洁省略了偏置项，且第二个非线性层在$F(x)+x$之后使用

注意到这个shortcut connection没有引入新的参数和多的计算复杂度

注意到$F$和$x$的维度必须相同，如果不相同，可以通过一个投影变换实现
$$y=F(x,\{W_i\})+W_{s}x$$
作者也提出可以在维度match的时候在$x$前加一个方阵$W_s$，但实验中表明恒等映射已经足够，$W_s$仅仅在维度不匹配时使用
每个building block中的层数大于等于两层（图例中是两层），作者观察到使用1层并不能带来什么好处，可能由于1层本身就是一个线性变换$y=W_{1}x+x$

网络结构

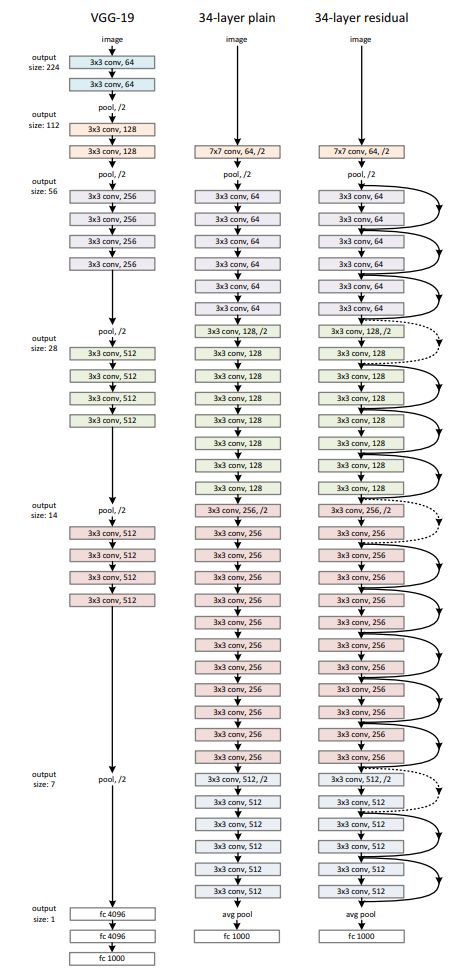
作者使用一个plain网络和一个ResNet来做对比，其中

• plain Network
  • 所有卷积之后输出的大小不变
  • 如果特征图长宽小一半，则卷积核的数量加倍（channel加倍）以保证每层计算复杂度一样
• Residual Network
  • 在plain Network的基础上加shortcut connections
  • 维度相同时，之间使用identity shortcuts
  • 如果维度增加了（channel），有两个选择：
    • (A) 0 padding
    • (B) 使用投影变换

注意其中的下采样均是由stride为2的卷积网络实现的，而非池化层

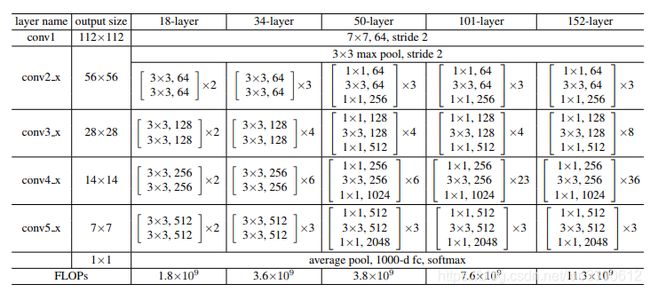
不同层的ResNet

层数不同的ResNet的区别如下

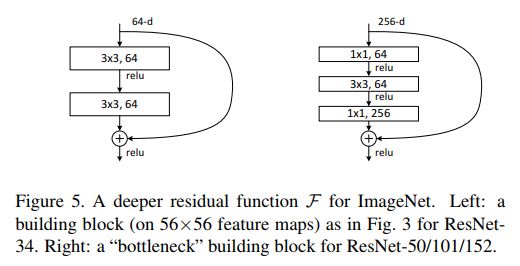
bottleneck是权衡之后的building block，更深的网络可以得到更好的结果，但是相比训练时间来说是不值得的

ResNet-50

用3层的block代替ResNet34中的2层block

ResNet101和ResNet152

使用更多的3层block得到

效果如何

plain Net和ResNet的对比

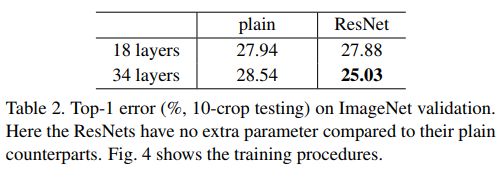
浅层的网络精度相差不多，但ResNet18收敛更快，随着层数增加，plain Net的误差反而上升，而ResNet的误差大大下降

shortcuts connection和不同层数的ResNet的对比（ImageNet）

三种shortcuts

• (A)0 padding
• (B)只在维度改变时使用投影
• ©所有shortcuts都使用投影
  
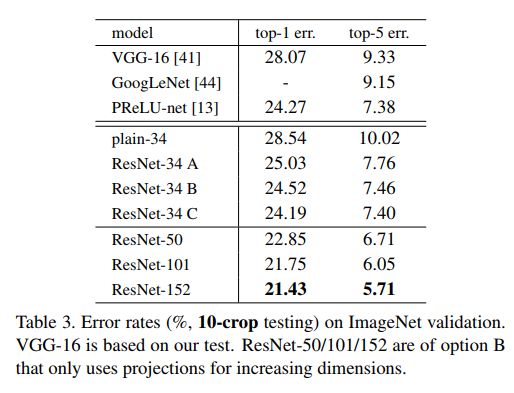
  结果表明三种方法的结果相差不多，C比AB好一点，但C引入了太多的参数，且ResNet50/101/152比ResNet34有更高的准确率

CIFAR-10

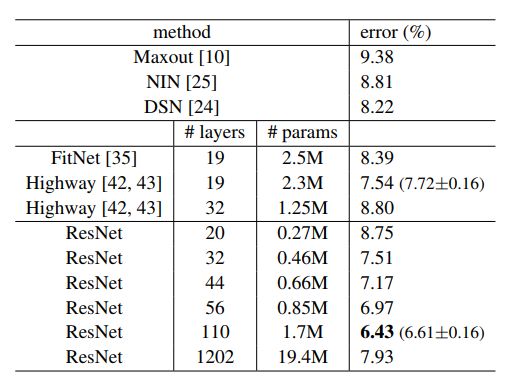
注意到ResNet1202虽然误差也很好，但是没有ResNet110好，可能是因为过拟合的原因

结论

• ResNet更容易优化
• 更容易使得网络更深以获得更高的准确率
• 以3.57%的top-5错误率赢得了2015年ILSVRC的冠军，获得了ImageNet detection，ImageNet localization，COCO detection 和COCO segmentation的冠军

存在什么不足

?

其他

术语

• FLOPS 每秒浮点运算次数

训练的细节

Image Net

• 图片随机将小的那一维resize成[256,480]中的值，然后crop成224*224
• 使用了standard color augmentation
• 在卷积之后激活之前使用batch normalization
• 使用SGD，初始学习率为0.1，当误差停滞的时候，将学习率除以10
• weight decay 0.0001，动量0.9
• 不使用dropout

CIFAR-10

• mini batch 128
• 初始学习率0.1，在32k和48k次迭代时除以10
• 在64k次迭代时终止

问题

具体地，A、B是怎么实现的？

本周小结

• 终于完成了拖欠三周的resnet论文的阅读
• 训练出初始的superpoint模型，卡在bug上未完成
• 学习opencv到百分之50，快到25%了

下周计划

• 阅读faster-cnn的论文
• 训练出MagicPoint
• 学习opencv上册到50%