深度学习之灾难性遗忘问题
深度学习之灾难性遗忘问题
健忘是一种病态,善忘是一种智慧。 ——写在前面
文章目录
- 深度学习之灾难性遗忘问题
- 1. 背景
- 2. What and Why 灾难性遗忘
- 首先回答第一个W: 什么是灾难性遗忘?
- 接着回答第二个W: 为什么会灾难性遗忘?
- 3. 现有的解决方法综述
- 3.1 Self-refreshing Memory Approaches
- 3.1.1 核心思想——递归网络的吸引子特性
- 3.1.2 方法介绍
- 3.1.3 一个例子
- 3.1.4 程序
- 3.2 知识蒸馏法
- 3.2.1 蒸馏神经网络
- 3.2.2 知识蒸馏方法
- 3.2.3 算法介绍
- 3.2.4 训练步骤
- 3.2.5 蒸馏loss
- 3.3 Transfer Techniques
- 4. 结语
- 参考文献
1. 背景
当你在看这篇博客的时候,就正在使用一个复杂的生物神经网络。你有一个约为876亿个神经元的高度互连的大脑帮你完成阅读、呼吸、运动和思考。你的每一个生物神经元都是生物组织和化学物质的有机结合。若不考虑其速度的话,可以说每个神经元都是一个复杂的微处理器。你的某些神经结构是与生俱来的,而其他一些则是在实践中形成的。
科学家们对生物神经网络工作机理有一定的认识。一般认为,包括记忆在内的所有生物神经功能,都存储在神经元和及其之间的连接上。学习被看作是在神经元之间建立新的连接或对已有的连接进行修改的过程。 早在20世纪60年代,科学家们就基于对生物神经网络工作机理认识,期望构造出像人类大脑一样容纳智慧、意识、记忆的人工神经网络。但均以失败告终。就连被大家推向神坛的深度学习在结构上、以及功能与生物神经网络都相去甚远。
与生物神经网络相比较,现有的深度学习存在诸多缺陷。灾难性遗忘就是缺陷之一。所谓的灾难性遗忘:即学习了新的知识之后,几乎彻底遗忘掉之前习得的内容。它使得人工智能体缺乏像生物一样不断适应环境以及增量式(持续)学习的能力。早在神经网络的远古时代,研究人员[1-2]就已经发现人工神经网络中存在这一问题了。直到现在,仍然有许多研究人员(例如… Goodfellow, yoshua Bengio等[3])偿试解决(缓解)深度学习中的灾难性遗忘问题。
2. What and Why 灾难性遗忘
首先回答第一个W: 什么是灾难性遗忘?
上面已经给出灾难性遗忘的定义,此处复述:灾难性遗忘即学习了新的知识之后,几乎彻底遗忘掉之前习得的内容。
具体描述:我们搭建了一个深度神经网络来学习识别各种动物。假定我们遇到了一个非常吝啬的数据提供者,每次只提供一种动物的数据,并在学习完成识别该动物后,将数据收缴上去;然后才给下一个动物的训练数据。有意思的现象出来了,这个神经网络在学习识别小狗后,让它识别之前学习过的小猫,它竟然识别不出来。这就是灾难性遗忘,它一直是深度学习领域一个比较严重的问题。
基于深度学习的智能体们就像陈列在书架上的一本本工具书,它利用预先收集好的静态的数据集学习,在学习过程结束后就是一种静态(没有生命)的存在。无法对新数据进行学习,如果硬塞给它学习,就会出现灾难性遗忘问题。当然,我们可将新数据加入到历史训练数据集中,用包含新旧训练数据的数据集对网络进行重新训练,可想而知,这样做法的学习效率是有多低!
在现实世界中,很多任务不可能一次性得到所有的训练数据(例如开放的环境、非特定的任务)。这就使得神经网络必须能够利用不断产生的新数据持续学习新知识,并且不遗忘之前所学过的重要内容。然而,持续学习却是人类以及其他生物与生俱来的能力。只有解决了灾难性遗忘问题,人工神经网络才有可能变成像人类一样强大的智能体,而不是摆在书架上一本本静态的工具书。
注意:深度强化学习的训练过程似乎不需要预先收集所有的训练数据,但是它的环境与任务都是封闭的。深度神经网络的结构是针对任务手工调整确定,并在训练、测试与利用时保持不变。我想强调的是,深度强化学习披上了强化学习利用机器人与环境交互的数据进行学习的外衣,让我们有种深度学习具备持续学习的能力,不存在灾难性遗忘的问题的错觉。首先,大部分深度强化学习成功的例子中的任务是特定的、环境的状态空间也是确定的。机器人在这样一个环境中,学习这一任务,相当于有一个已经确定的有边界的数据集,每一个训练数据都是按特定的概率分布在这个数据集中采样得到的。并且,类似于有监督的深度学习,喂给深度强化学习的交互数据也是会重复出现,通过对神经元不断的刺激完成学习的。最近,有研究人员利用深度强化学习对多任务进行学习,作者明确指出首先需要面的问题就是深度神经网络的灾难性遗忘问题,里面有非常明显的缓解灾难性遗忘问题的机制。
接着回答第二个W: 为什么会灾难性遗忘?
深度学习的灾难性遗忘问题是深植于它的基因,是无法解决的问题,只能通过各式各样的机制、策略来缓解。
为什么说是深植于它的基因里呢?神经网络由网络结构与网络参数构成。不凑巧的是,深度学习在结构与参数两方面都植入了灾难性遗忘的基因:
- 深度学习的结构一旦确定,在训练过程中很难调整。神经网络的结构直接决定学习模型的容量。固定结构的神经网络意味着模型的容量也是有限的,在容量有限的情况下,神经网络为了学习一个新的任务,就必须擦除旧有的知识。
- 深度学习的隐含层的神经元是全局的,单个神经元的细小变化能够同时影响整个网络的输出结果。另外,所有前馈网络的参数与输入的每个维度都相连,新数据很大可能改变网络中所有的参数。我们知道,对于本身结构就已经固定的神经网络,参数是关于知识的唯一变化量。如果变化的参数中包含与历史知识相关性很大的参数,那么最终的效果就是,新知识覆盖了旧的知识。
其它类型的人工神经网络如果也存在灾难性遗忘问题,也逃不掉以上两种原因(或其中之一)。
备注:那么,有没有不含灾难性遗忘问题的人工神经网络,当然有:例如增量式径向基函数网络、自组织增量学习网络等代表的宽度学习就不存在灾难性遗忘问题。但它们又存在其他非常严重的问题,使其不具备到类人的持续学习能力,本文暂不表。
3. 现有的解决方法综述
现有的灾难性遗忘问题解决方法大致可以分为两派:参数派与结构派。其中,参数派主张对深度学习进行修补,结构派主张提出新的人工神经网络模型。此部分主要针对深度学习的灾难性遗忘问题进行综述,因此主要介绍参数派的方法,不过多涉及结构派。
新数据会修改与历史知识相关的重要神经元的参数,这是造成深度学习灾难性遗忘的根本原因。大致有四种方法:1) 利用新数据训练的同时,不断用包含历史数据相关的信息刺激神经元,形成一种竞争,从而使历史知识相关的重要神经元的参数尽可能少的受影响,同时也保证了新知识能够被学习;通常称为Self-refreshing Memory Approaches[5];2)在开始训练新数据前,利用旧网络对新数据进行预测得到虚拟的训练数据【可以看作是旧网络的一个回忆】,目标函数中包含新旧网络的参数约束,每训练一个新数据,利用所有的虚拟数据约束旧参数,抑制遗忘;这类方法被称为知识蒸馏法[6];3)[7]从另一个角度来约束参数的变化,文中认为参数是一个概率分布,只要在这个分布的核心地带,对于该任务就是可行的,不同的任务对应不同的概率分布,如果能找到两个分布重叠的部分,并将参数约束到这个区域,那么这一参数不就可以对这些任务都有效吗,这类方法被称之为Transfer Techniques法[7]。4)第四类,我称它为其它方法,例如保留所有的历史数据,研究评判重要数据的技术,只保留那些重要的,信息量大的数据。这只是保留所有历史数据的一个改进版本,只要评判方法合理,肯定也能缓解灾难遗忘问题,本文对这一类方法就不介绍。下面只介绍前三种方法。
3.1 Self-refreshing Memory Approaches
关于这类方法,具有代表性的文章为[4]。
3.1.1 核心思想——递归网络的吸引子特性
这类方法的核心思想是利用不断递归的混响过程来生成虚拟的知识实体(用来提醒学习器,以防止遗忘)。这个过程能够通过一个随机的输入收敛到网络的吸引状态与输出。这样的吸引状态与输出更能刻画之前学到的知识。
一个递归的自编码神经网络具备的一个重要特性——attractor 吸引子。
具体描述如下:
对于一个自编码器(期望的输出就是输入本身),我们利用一个状态空间子集包含的状态来训练这个自编码器,训练结束后,我们用不在这个状态空间的状态输入到网络中,得到输出,然后将得到的输出又作为输入,经过若干次迭代后,网络的输出会被吸引到训练的状态子空间中。
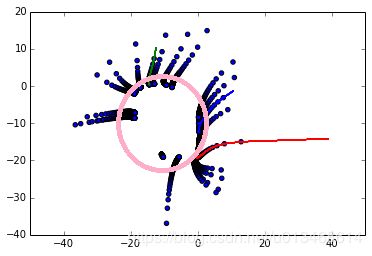
现在将如下图粉色圏内的二维状态以随机采样的方式输入到自编码器中,直到训练收敛。然后我将粉色圏外的20个状态输入到训练好的自编码器中,并不断循环迭代。下图画出每个输入数据吸引轨迹,我们发现最终都吸引到了训练所用到的状态子空间中。Self-refreshing Memory Approaches主要就是利用了自编器神经网络的这一特点,来隐式的存储历史数据的信息,以备将来训练新数据时,能够生成用于唤醒历史知识的虚拟训练数据。
3.1.2 方法介绍
以上是Self-refreshing Memory Approaches主要思想。
文章的摘要简述如下:
本文方法主要是利用一个self-refreshing memory自更新的存储器来存储已经学到的知识,并利用该存储的知识来不断“提醒”学习器不要忘记之前的学到的知识,从而达到避免灾难性遗忘的目的。而之前最粗暴的作法是,提取能很好代表之前知识的训练样本集,并且在训练新样本的时候,不断的利用这个代表之前知识的样本集对学习器进行“提醒”功能,从而达到避免灾难性遗忘的目的。而提取并存储这样的代表样本集即耗费时间又浪费空间。本文直接利用一个能自我更新的存储器来存储现今学到的所有知识,并且在新样本训练学习器的期间,不断对学习器进行“提醒”。
文章最核心的一张图如下:
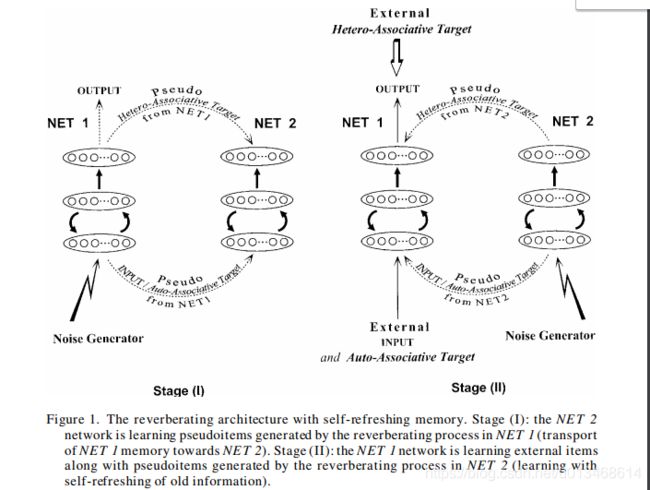
文章提出了一个dual-network结构,由两个相互偶合的多层网络 N E T 1 NET_1 NET1与 N E T 2 NET_2 NET2组成。对于每一个网络,输入层与隐含层以及隐含层与输出层都是全连接的。与普通网络不同的是,此处隐含层到输入层也是全连接的,意思是输入层与隐含层是双向的,当然不同的方向对应的是不同的连接权值。 N E T 1 NET_1 NET1即能够学习外部(环境的)的信息,也能够学习 N E T 2 NET_2 NET2发布的信息。而 N E T 2 NET_2 NET2则只能学习 N E T 1 NET_1 NET1发布的信息。此处利用BP算法来更新两个网络的参数。当一个从环境中得到的新样本external input–target输入到 N E T 1 NET_1 NET1中,输入输出的误差,以及输入以及从隐含层到输出层的计算值的误差(这个结构相当于自编码网络)都需要被用来更新网络。这样,输入-隐含-输出 相当于异联想,而 输入-隐含-输入 相当于自联想。 N E T 2 NET_2 NET2也是利用同样的训练方法与方式。此处值得强调,自联想与异联想都是需要的。
下面利用一个简单的学习过程来说明,怎么利用该结构实现避免灾难性遗忘的目的。
一个初始的状态如, N E T 1 NET_1 NET1已经对给定的数据集完成学习任务,此时 N E T 2 NET_2 NET2应该还是“空”的状态,参数还是处于随机设定的状态。假定此时进入第一阶段,denoted stage(如图左): N E T 1 NET_1 NET1此时停止接受环境中的样本,但是 N E T 1 NET_1 NET1仍处理工作状态。利用噪声生成器随机的生成一个随机的激发信号(seed),对于该激发输入信息按照input-hidden-input路线计算最终的值,第一次得到的输出层激活值被再次注入隐含层,从而得到一个输出和一个输入活跃值。第二次的输入活跃值又被重新注入到隐含层,得到下一个输出以及输入活跃值,一直这样重复 R R R次,得到最终的输出值与输入活跃值作为 N E T 2 NET_2 NET2的训练样本。第二阶段(图右): N E T 1 NET_1 NET1学习新样本的同时,利用 N E T 2 NET_2 NET2生成的“提醒”样本来对 N E T 1 NET_1 NET1进行不断复习。
简而言之,本方法利用两个结构上一模一样的网络(替身网络与真身网络)来克服灾难性遗忘的问题。学习过程由两个周期迭代(训练步与梳理步)的步骤组成。在训练步时,真身网络同时利用替身网络生成的虚拟数据以及新数据学习新参数,学习稳定后进入第二步。第二步时,将真身网络的现有知识传授给替身网络(文中采用了比较简单的方法:直接将真身网络的参数copy给替身网络)。
本人利用一个简单的序列训练数据来测试方法的有效性。
3.1.3 一个例子
训练数据集
利用两组数据集(生成于函数 y = s i n ( x 1 ) x 1 + x 2 10 y=\frac{sin(x_1)}{x_1}+\frac{x_2}{10} y=x1sin(x1)+10x2) S 1 , S 2 S_1,S_2 S1,S2。先利用 S 1 S_1 S1对模型进行训练,训练一定步数后,再利用 S 2 S_2 S2对模型进行训练。
- S 1 : x 1 = [ − 20 , 0 ] , x 2 = [ − 20 , 0 ] S_1:x_1=[-20,0],x_2=[-20,0] S1:x1=[−20,0],x2=[−20,0]
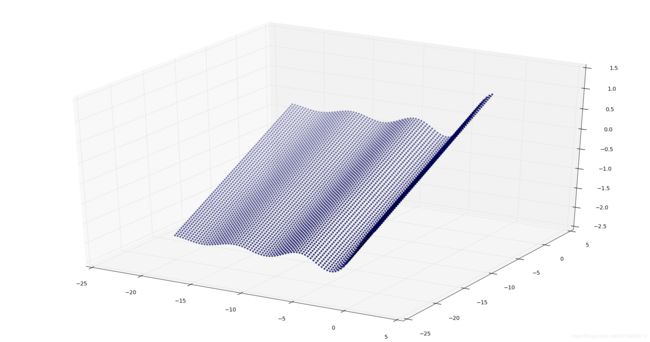
- S 2 : x 1 = [ 0 , 20 ] , x 2 = [ − 20 , 0 ] S_2:x_1=[0,20],x_2=[-20,0] S2:x1=[0,20],x2=[−20,0]
对照实验
-
原始方法:只利用一个模型先对数据集 S 1 S_1 S1学习,然后对 S 2 S_2 S2学习,最后测试对 S 1 S_1 S1数据集的拟合误差。
-
本文方法:利用两个模型, N E T 1 NET_1 NET1用于学习新的知识, N E T 2 NET_2 NET2用于存储当前学习到的知识,并对 N E T 1 NET_1 NET1进行‘提醒’,以防止灾难性遗忘。
结果
- 原始方法:各数据集的训练步长都为60000
| S 1 S_1 S1 | S 2 S_2 S2 | re-fitting S 1 S_1 S1 | |
|---|---|---|---|
| MSE | 0.042918288146 | 0.03675510078 | 0.453335550511 |
- 文中方法:各数据集的训练步长都为60000
| S 1 S_1 S1 | S 2 S_2 S2 | re-fitting S 1 S_1 S1 | |
|---|---|---|---|
| MSE | 0.042918288146 | 0.0409538226834 | 0.0502870424298 |
表中给出每个子训练过程后的均方根误差(MSE)。模型对每组数据都能够拟合的很好,但是经过对子数据集S2的学习后,重新检测对S1数据集的拟合误差,我们发现原始方法MSE变的非常大(0.04 → \rightarrow → 0.45),而文中的方法只是稍稍变化了一点点(0.04 → \rightarrow → 0.05),这说明文中的方法的确缓解了神经网络的灾难性遗忘问题。
3.1.4 程序
程序1:原始方法
import numpy as np
from collections import namedtuple
import torch
import torch.nn.functional as F
from torch.autograd import Variable
import torch.nn as nn
from sklearn import preprocessing
from sklearn.decomposition import PCA
import torch.optim as optim
import time
import random
random.seed(0)
FloatTensor = torch.FloatTensor
LongTensor = torch.LongTensor
ByteTensor = torch.ByteTensor
Tensor = FloatTensor
def data_generator(x1, x2):
return np.sin(x1)/x1+x2/10
Transition = namedtuple('Transition',
('state', 'label'))
class ReplayMemory(object):
def __init__(self, capacity):
self.capacity = capacity
self.memory = []
self.position = 0
def push(self, *args):
"""Saves a transition."""
if len(self.memory) < self.capacity:
self.memory.append(None)
self.memory[self.position] = Transition(*args)
self.position = (self.position + 1) % self.capacity
def sample(self, batch_size):
return random.sample(self.memory, batch_size)
def __len__(self):
return len(self.memory)
""" MLP """
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()
self.fc1 = nn.Linear(2, 100)
self.fc2 = nn.Linear(100, 3)
def forward(self, x):
x = F.sigmoid(self.fc1(x))
return self.fc2(x)
data = ReplayMemory(3000)
for i in range(3000):
x1 = 20.0*np.random.rand(1)-20.0
x2 = 20.0*np.random.rand(1)-20.0
x = np.array([x1[0], x2[0]])
y = data_generator(x1[0], x2[0])
label = np.array([x1[0], x2[0], y])
data.push(Tensor([x]),Tensor([label]))
model = Net()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
tic = time.time()
for i in range(60000):
# get the inputs
transitions = data.sample(25)
batch = Transition(*zip(*transitions))
state_batch = Variable(torch.cat(batch.state))
label_batch = Variable(torch.cat(batch.label))
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = model(state_batch)
loss = criterion(outputs, label_batch)
loss.backward()
optimizer.step()
toc = time.time()
print("the time cost is:"+str(toc-tic))
print('Finished Training')
x1_axis = np.linspace(-20,-0.001,75)
x2_axis = np.linspace(-20,-0.001,75)
X1 = []
X2 = []
true_y = []
pre_y = []
for m in range(len(x1_axis)):
for n in range(len(x2_axis)):
X1.append(x1_axis[m])
X2.append(x2_axis[n])
x = np.array([[x1_axis[m], x2_axis[n]]])
inputs = Variable(torch.Tensor(x))
outputs = model(inputs)
true_y.append(data_generator(x1_axis[m],x2_axis[n]))
label = outputs.data[0].numpy()
pre_y.append(label[-1])
X1 = np.array(X1)
X2 = np.array(X2)
true_y = np.array(true_y).ravel()
pre_y = np.array(pre_y).ravel()
error = np.sum(np.abs(true_y-pre_y))/len(true_y)
print('error: '+str(error))
程序2:Self-refreshing Memory
import copy
import time
new_model = copy.deepcopy(model)
new_optimizer = optim.Adam(new_model.parameters(), lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
old_model = copy.deepcopy(model)
old_optimizer = optim.Adam(old_model.parameters(), lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
tc = time.time()
def generate_new(batch_size):
test_x = 40*np.random.rand(batch_size,2)-20
for i in range(100):
inputs = Variable(torch.Tensor(test_x))
outputs = new_model(inputs)
label = outputs.data.numpy()
test_x[:,0] = label[:,0]
test_x[:,1] = label[:,1]
X = test_x
Y = label
return Tensor(X),Tensor(label)
def generate_old(batch_size):
test_x = 40*np.random.rand(batch_size,2)-20
for i in range(100):
inputs = Variable(torch.Tensor(test_x))
outputs = old_model(inputs)
label = outputs.data.numpy()
test_x[:,0] = label[:,0]
test_x[:,1] = label[:,1]
X = test_x
Y = label
return Tensor(X),Tensor(label)
data = ReplayMemory(3000)
for i in range(3000):
x1 = 20.0*np.random.rand(1)-0.0
x2 = 20.0*np.random.rand(1)-20.0
x = np.array([x1[0], x2[0]])
y = data_generator(x1[0], x2[0])
label = np.array([x1[0], x2[0], y])
data.push(Tensor([x]),Tensor([label]))
tic = time.time()
for i in range(60000):
# get the inputs
transitions = data.sample(10)
batch = Transition(*zip(*transitions))
extern_state = torch.cat(batch.state)
extern_label = torch.cat(batch.label)
# new_active_state, new_active_label = generate_new(10)
# state_batch = Variable(extern_state)
# label_batch = Variable(extern_label)
state_batch = Variable(torch.cat((extern_state,new_active_state),0))
label_batch = Variable(torch.cat((extern_label,new_active_label),0))
# zero the parameter gradients
old_optimizer.zero_grad()
# forward + backward + optimize
outputs = old_model(state_batch)
loss = criterion(outputs, label_batch)
loss.backward()
old_optimizer.step()
old_active_state, old_active_label = generate_old(10)
old_state_batch = Variable(old_active_state)
old_label_batch = Variable(old_active_label)
new_optimizer.zero_grad()
old_outputs = new_model(old_state_batch)
loss = criterion(old_outputs, old_label_batch)
loss.backward()
new_optimizer.step()
toc = time.time()
print("the time cost is:"+str(toc-tic))
print('Finished Training')
test主程序
# x1_axis = np.linspace(-20,-0.001,75)
# x2_axis = np.linspace(-20,-0.001,75)
x1_axis = np.linspace(0.001,20,75)
x2_axis = np.linspace(-20,-0.001,75)
X1 = []
X2 = []
true_y = []
pre_y = []
for m in range(len(x1_axis)):
for n in range(len(x2_axis)):
X1.append(x1_axis[m])
X2.append(x2_axis[n])
x = np.array([[x1_axis[m], x2_axis[n]]])
inputs = Variable(torch.Tensor(x))
outputs = old_model(inputs)
true_y.append(data_generator(x1_axis[m],x2_axis[n]))
label = outputs.data[0].numpy()
pre_y.append(label[-1])
X1 = np.array(X1)
X2 = np.array(X2)
true_y = np.array(true_y).ravel()
pre_y = np.array(pre_y).ravel()
error = np.sum(np.abs(true_y-pre_y))/len(true_y)
print('error: '+str(error))
3.2 知识蒸馏法
3.2.1 蒸馏神经网络
蒸馏神经网络[8],是14年Hinton提出来的一个概念。为了更好的理解知识蒸馏法如何缓解灾难性遗忘问题,请先阅读这篇CSDN博客蒸馏神经网络到底在蒸馏什么?(设计思想篇)。具体内容可以总结如下:
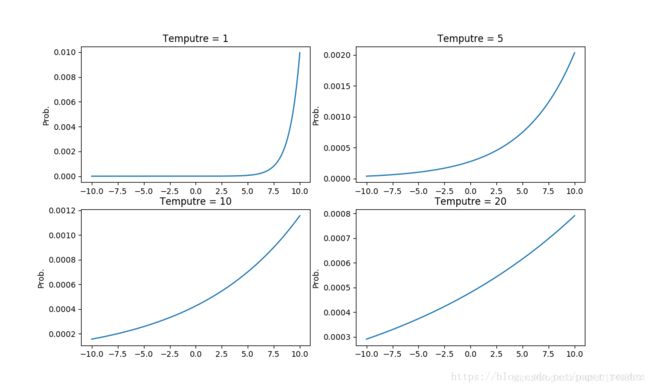
原始的蒸馏神经网络是为了提高深度学习的训练效率与减小网络模型结构的复杂程度,减小深度学习在轻量级的移动平台上的时间与空间花销。[8]的应用背景是one-hot编码label的分类问题。首先在计算能力强的平台上训练一个复杂的深度神经网络,网络的输出是一个softmax函数产生的概率分布,softmax函数中有一个决定输出概率分布均匀程度的值——温度值T。训练复杂网络时,温度值设定为一个较大的值,期望得到一个较均匀的分布。文中强调的是,要用大量的数据训练这个复杂的网络。复杂网络训练结束后,接着我可以这样更加有效率的训练一个模型结构更简单的网络。一般简单网络需要面对更加具体的任务,是要被应用的。针对它要应用的任务,我们会有一些数据(数据量远比训练复杂网络时的数据量小),首先利用复杂网络预测这些数据的输出。现在我们有两套训练简单网络的数据:a)状态-真实输出(one-hot label);b)状态-复杂网络预测的概率输出(连续值)。先利用数据集b训练简单网络至稳定,然后利用数据集a继续训练。与标准步骤多出的部分就是先利用复杂网络预测的数据输出来引导简单网络,由于预测的输出值是概率值,连续的,因此用这类数据使网络更易收敛。此时,简单网络已经快速的学到一些粗糙的知识,在此基础上利用真实数据集继续训练就快得多了。(下图是温度值T取不同值时,softmax函数输出的曲线。当取值较大时T=20,函数曲线变化平缓,分布较均匀。)
简而言之,蒸馏神经网络的核心依据有两点:1) 训练完成的神经网络包含历史数据的输出分布信息; 2) 神经网络具有相似的输入会得到相似的输出的特点。
3.2.2 知识蒸馏方法
接下来,介绍如何利用知识蒸馏技术缓解灾难性遗忘问题。
首先,给出下面这张信息丰富的图。
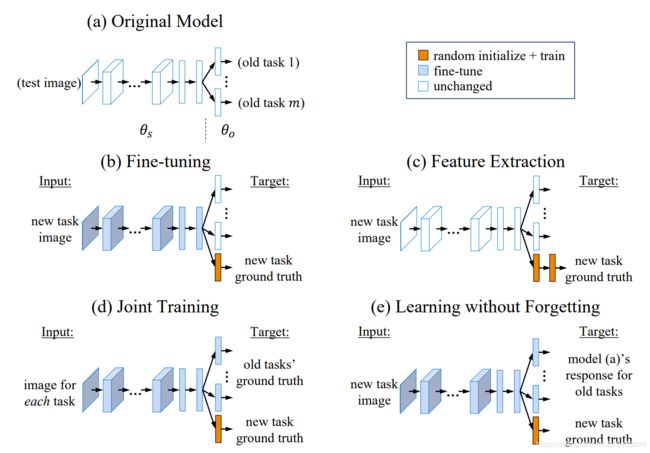
上图的(b)-(e)分别是传统深度学习向持续学习的扩展方法。知识蒸馏法对应(e)。这部只介绍(e),在后面再介绍(b)-(d)。如图(e)所示,应用背景为多任务学习,并且学习是增量式的。各任务只有输出的全连接层是独立的,其他的特征提取,中间的隐含层都是共享的。假定此时,网络已经学完第n个任务,要开始学习第n+1个任务。蒸馏法通过对共享参数进行微调来实现对新知识的学习。观察(d)与(e),两者从结构图上好像完全一样,都是对共享参数进行微调。他们不同的地方就是怎么保证不遗忘。(d)的做法比较粗暴,直接利用联合历史数据与新数据一起训练这个网络,意味着需要不断存储历史数据。然而,蒸馏法不用存储历史数据。
3.2.3 算法介绍
下面利用下图所示的算法来说明论文[6]是如何利用"蒸馏技术"来缓解灾难性遗忘问题的。对于一个针对增量式多任务的深度神经网络,有共享参数 θ s \theta_s θs。为了方便与当前要学的新任务区分,我们把旧(old)任务相关的输出全连接参数记为 θ o \theta_o θo,把新(new)任务对应的输出全连接参数记为 θ n \theta_n θn。学习的目标为网络的所有参数( θ s , θ o , θ n \theta_s,\theta_o,\theta_n θs,θo,θn)能够在新的和旧的任务上都有很好的表现(见图e)。

问题的重点在共享参数 θ s \theta_s θs:为了适应新任务,它必须得调整;为了不遗忘旧任务,它最好保持不变。有了矛盾,就得解决对不对。即然一定得调整,那我们就调整好了,但得加入一些约束。
上图算法最后一行为文中的目标函数,红下划线标记的为新加入的约束项(被称为蒸馏loss),第二项与第三项与标准深度学习的目标函数相同。
我们来看看这一项是如何起作用的。
想法:要保证旧任务不遗忘,就需要旧任务相关的数据能够在新数据训练时不断刺激强化神经元,抑制遗忘发生。我们的高追求不允许采用记录历史数据的低级方式。旧任务的参数包含历史数据的分布信息,我们可以利用旧任务的参数生成一些虚拟的数据,这些数据相当于分布的采样。在训练新数据时,充分考虑这些虚拟数据。【这一想法与self-refreshing memory[4-5]不谋而合】
在这个新的网络中,我们希望对于原来的任务其输出能和原来的网络的输出接近。采用上面的“回忆刺激神经元抑制遗忘”的想法,我们首先得产生这样的虚拟数据。还记得上面介绍的蒸馏神经网络吗?它直接将新数据输入到训练好的复杂网络中得到输出,并将输入—复杂网络预测的输出对组成新的数据集。我们也采用这样的做法产生需要的虚拟数据,只需将复杂网络替换成旧网络。与原始蒸馏神经网络的目的不一样,那里是加速简单网络的训练与稳定性,此处是用来缓解网络对新任务学习的灾难性遗忘问题。
3.2.4 训练步骤
1)记录新的数据在原始的网络上的输出 Y o ^ \hat{Y_o} Yo^(与参数 θ s θ o θ_s θ_o θsθo相关);
2)对于新增的类,我们增加相应的FC的节点个数,并随机初始化权重 θ n θ_n θn;
3)我们训练网络并优化其loss在所有的分类上有最小的loss。在训练的时候,我们首先freeze掉 θ s θ_s θs 和 θ o θ_o θo,然后训练 θ n θ_n θn 直到其收敛,然后我们在训练所有的 θ s θ_s θs, θ o θ_o θo和 θ n θ_n θn直到其收敛。
3.2.5 蒸馏loss
L o l d ( y o , y o ^ ) = − H ( y o ′ , y ^ o ′ ) = − ∑ i = 1 l y o ′ ( i ) l o g y ^ o ′ ( i ) L_{old}(y_o,\hat{y_o})=-H(y'_o,\hat{y}'_o)=-\sum_{i=1}^l y'^{(i)}_o log\hat{y}'^{(i)}_o Lold(yo,yo^)=−H(yo′,y^o′)=−i=1∑lyo′(i)logy^o′(i)
此处, l l l为新数据的个数, y o ′ ( i ) y'^{(i)}_o yo′(i)为旧神经网络预测的输出, y ^ o ′ ( i ) \hat{y}'^{(i)}_o y^o′(i)为经过softmax函数规范化的概率形式。具体计算如下式:
y o ( i ) = ( y o ( i ) ) 1 / T ∑ j ( y o ( j ) ) 1 / T , y ^ o ( i ) = ( y ^ o ( i ) ) 1 / T ∑ j ( y ^ o ( j ) ) 1 / T y_{o}^{(i)}=\frac{\left(y_{o}^{(i)}\right)^{1 / T}}{\sum_{j}\left(y_{o}^{(j)}\right)^{1 / T}}, \quad \hat{y}_{o}^{(i)}=\frac{\left(\hat{y}_{o}^{(i)}\right)^{1 / T}}{\sum_{j}\left(\hat{y}_{o}^{(j)}\right)^{1 / T}} yo(i)=∑j(yo(j))1/T(yo(i))1/T,y^o(i)=∑j(y^o(j))1/T(y^o(i))1/T
本质上[5]与[6]是一样的,[5]采用一个替身神经网络来产生虚拟的数据(随机输入产生的),它是对旧知识的随机采样,我们用它来不断刺激神经元,帮助回忆,抑制遗忘。[6]将新数据输入到旧网络产生虚拟数据,目标函数中包含旧网络的约束项,每当训练一个新数据,同时利用所有的虚拟数据来对旧知识进行回忆。
3.3 Transfer Techniques
首先给出论文[7]中的第一张图。作者认为对于每个任务,其有效的参数应该是一个概率分布的形式。图中浅红色表示旧任务对应的参数分布,浅绿色对应新任务的参数分布。如果只是单纯的将两分布的均值求平均,最终的值可能即不是旧任务的可行参数,也不是新任务的可行参数。如何综合考虑旧参数与新数据得使得参数迁移到大家都满意的值是这篇文章的突破灾难性遗忘问题的核心思想。
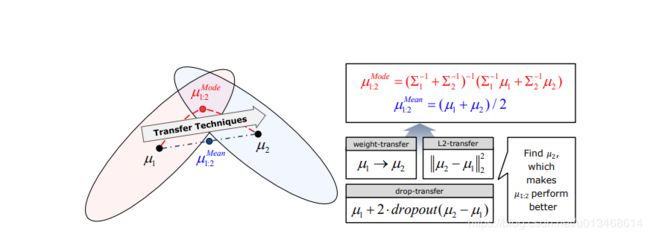
如果只是简单将任务的weight每个维度都看作同等重要的,那么就完全忽略掉了loss function的形态,从而会得到一个不好的结果。因此,论文考虑了参数分布的二阶矩信息(方差)。作者还提出了3种方式来逐步地迁移weight:1)weight-transfer;2)L2-transfer;3)drop-transfer。 具体细节就不展开,有兴趣的读者可以参考原始论文[7]。
本来想乘放高温假好好写一下这篇博客的,耐何最近玩心重了点,最后收尾也只能草草了。这部分的核心想法给出来了,想要了解更多,可以看原论文。我在网上找了一圈,没有发现对这篇论文详细的解读,所以,只能靠自己了。
4. 结语
本文首先引出神经网络中比较严重并亟待解决的问题——灾难性遗忘问题。尝试给出了灾难性遗忘的原因,并综述了现有深度学习中针对灾难性遗忘的研究。本文没有过多涉及新神经网络结构派的内容。如果一个新的结构能够避免灾难性遗忘,那么就不需要对它强调这一问题,它有更重要的事情要做。那如果,这个新网络结构不能够避免遗忘,那讲它又有何用。这一原因,本人觉得灾难性遗忘综述没必要加入新结构派的内容。
本文内容仅仅是本人平时猎奇收集的内容,并没有深入研究,许多描述、理解、观点可能不尽清晰、正确。还请各位包涵,也欢迎指出文中不当之处。谢谢!记录本就是为了自己的快速回忆,从而避免灾难性遗忘。本文的内容只关于健忘,善忘也是非常重要的研究课题,特别是处于大数据、知识大爆炸时代的我们与我们创造的。我仍想用开头的那一句结尾:健忘是一种病态,善忘是一种智慧。
参考文献
[1] McCloskey, M., & Cohen, N. J. (1989). Catastrophic interference in connectionist networks: The sequential learning problem. Psychology of learning and motivation, 24, 109-165.
[2] French, R. M. . (1999). Catastrophic forgetting in connectionist networks. Trends in Cognitive Sciences, 3(4), 128-135.
[3] Goodfellow, I. J., Mirza, M., Xiao, D., Courville, A., & Bengio, Y. (2013). An empirical investigation of catastrophic forgetting in gradient-based neural networks. arXiv preprint arXiv:1312.6211.
[4] Ans B, Rousset S. Neural networks with a self-refreshing memory: Knowledge transfer in sequential learning tasks without catastrophic forgetting[J]. Connection Science, 2000, 12(1):1-19.
[5] Shmelkov K, Schmid C, Alahari K. Incremental Learning of Object Detectors without Catastrophic Forgetting[J]. 2017.
[6] Li, Z., & Hoiem, D. (2016). Learning without forgetting. In ECCV2016
[7] Lee, S. W., Kim, J. H., Ha, J. W., & Zhang, B. T. (2017). Overcoming Catastrophic Forgetting by Incremental Moment Matching. In NIPS2017
[8] Hinton, Geoffrey, Oriol Vinyals, and Jeff Dean.“Distilling the knowledge in a neural network.” arXiv preprint arXiv:1503.02531 (2015)