决策树的特征选择之1：香农熵、基尼指数、误分类误差

特征选择是决策树学习的重要内容，本文讨论的特征指标是香农熵、基尼指数和误分类误差。

不纯度度量

决策树学习的关键在如何选择最优划分属性。一般而言，随着划分过程不断进行，我们希望决策树的分支结点所包含的样本尽可能属于同一类别， 即结点的 “纯度”（purity）越来越高。在分类树中，划分的优劣用不纯度度量（impurity-measure）定量分析。
对于结点m，令N_m为到达结点m的训练实例数，对于根结点，N_m为N。N_m个实例中有N_mⁱ个属于C_i类，而$\sum$N_mⁱ=N_m. 当一个实例到达了结点m则它属于C_i类的概率估计为：

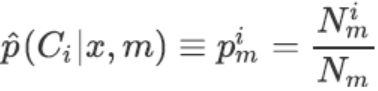
熵函数（香农熵）

在二分类问题中，如果对于所有的i，p_mⁱ为0或1：当到达结点m时，所有实例都不属于C_i类，则p_mⁱ为0。反之，如果所有实例都属于C_i类，则p_mⁱ为1。如果此时划分是纯的，则我们不需要再进一步划分，并可以添加一个叶结点，用p_mⁱ为1的类标记。
我们可以将任意结点的类分布记作（p₀,p₁），其中p₁=1-p₀。选择最佳划分的度量通常是根据划分后叶结点不纯性的程度。不纯度越低，类分布就越倾斜。例如，类分布为(0,1)的结点具有零不纯性，而均衡分布的(0.5,0.5)的结点具有最高的不纯性。一种度量不纯性的函数是熵函数（entropy）：

若p=0,则

在信息论与概率统计中，熵是表示随机变量不确定性的度量。这里我们使用的熵，也叫作香农熵，这个名字来源于信息论之父 克劳德·香农。
为了计算熵，我们需要计算所有类别所有可能值包含的信息期望值（数学期望），即上述公式。对于二分类问题，如果p¹=1而p²=0，则所有的实例都属于C_i类，熵为0。如果p¹=p²=0.5，熵为1。

但是，熵并非是唯一可能的度量。对于二分类问题，其中 p¹=p,p²=1-p，函数$\varphi$(p,1-p)是非负函数，度量划分的不纯度，如果满足如下性质：
对于任意 p$\in$[0,1]，$\varphi$(1/2,1/2)$\ge$(p,1-p) 。
$\varphi$(0,1)=$\varphi$(1,0)=0。
当p在[0,1/2]上时$\varphi$(p,1-p)是递增的，而当p在[1/2,1]上时$\varphi$(p,1-p)是递减的。

不纯度度量的函数公式

熵（Entropy）

$\varphi$(p,1-p) = -plog₂p-(1-p)log₂p

函数Entropy(m)是K>2个类的推广。

基尼指数（Gini index）

$\varphi (p,1-p)=1-{\sum }_{i=1}^m{p}_i^2$

误分类误差（Classification error）

$\varphi$(p,1-p) = 1-max(p,1-p)
这些都可以推广到K>2类，并且给定损失函数，误分类误差可以推广到最小风险。
下图显示了二元分类问题不纯性度量值的比较，p表示属于其中一个类的记录所占的比例。从图中可以看出，三种方法都在类分布均衡时（即当p=0.5时 ）达到最大值，而当所有记录都属于同一个类时（p等于1或0）达到最小值。

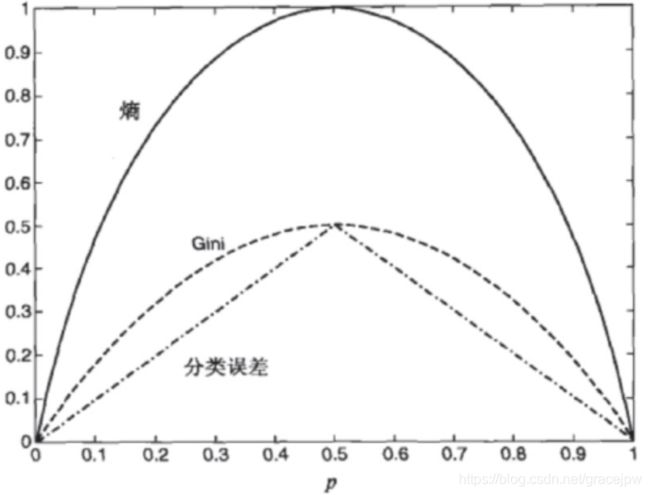
三种不纯性度量方法的计算实例：



从上面的例子及图中可以看出，不同的不纯性度量是一致的。根据计算，结点N₁具有最低的不纯性度量值，然后依次是N₂ , N₃。虽然结果是一致的，但是作为测试条件的属性选择仍然因不纯性度量的选择而异。
熵越高，信息的不纯度就越高，则混合的数据就越多。

香农熵的代码实现

#香农熵的代码实现
def calEnt(dataSet): #dataSet:原始数据集
    n = dataSet.shape[0] #数据集总行数
    iset = dataSet.iloc[:,-1].value_counts()#对标签列（最后一列）的值类别进行统计
    p = iset/n #每类标签占比
    ent = (-p*np.log2(p)).sum() #ent:香农熵的值 Entropy=sum(-p*log2(p))
    return ent

# 创建数据集
def createDataSet():
  row_data = {'accompany':[0,0,0,1,1],
             'game':[1,1,0,1,1],
             'bad boy':['yes','yes','no','no','no']}
  dataSet = pd.DataFrame(row_data)
  return dataSet

#生成数据集
dataSet = createDataSet()

#计算香农熵
calEnt(dataSet)

运行结果

0.9709505944546686