决策树(Decision Tree)
接上一篇:一文读懂L-BFGS算法
决策树在机器学习中一般不会单独使用,我们往往会使用基于决策树的另一个强大算法:随机森林.但是不了解决策树,咋学随机森林呢.所以我们这一节先学习决策树,下一节讲随机森林.
本文主要分一下几点:
1-决策树简介
2-生成决策树
3-确定分裂条件与分支数
4-叶子节点如何表达
5-什么时候停止分裂
6-代码实现
1-决策树简介
我认为决策树和随机森林是机器学习中最容易理解的算法,因为它的构思同我们大脑是思考方式非常相同.比如决定下班是否学习这件事情,人们的大概思路如下:
a.看一下今天下班的时间是几点,一般早一些是18:30,晚一些的是21:30.
b.如果下班时间在18:30和21:30之间,那约女神吃饭就有些晚了,女神都吃过饭了,可是睡觉又太早.所以这个时间段内选择学习.
c.如果是18:30之前下班,可以考虑约一下女神,如果约到了就去约会,约不到就去学习.
d.下班时间晚于21:30,这个时间久很晚了,如果最近两天面试被虐了或者最近两天有一个面试,自己还是要坚持一下学习的,如果没有,那就洗洗睡了.
以上思考的过程我们可以用下面的树形结构来表示:
上图其实就是一棵解决现实中问题的决策树.通过树结构可以很容易的看到影响我们是否学习的因素一共有三个,分别是下班时间,是否有约会和最近是否参加过或需要参加面试.虽然树的第二个分支我们用的是面试,但是博主并不是提倡程序员经常换工作.珍惜眼前的工作才是主要的.
言归正传,决策树中quittingtime是第一个分支点,我们称为根节点,根节点以外的has a date 和deadline节点成为子节点,显示最终分类结果的节点N/Y成为叶子节点.决策树符合人类的思考方式,是否还有其他优点呢?下边我们总结一下决策树的特点:
a.可解释性强
b.可处理非线性问题
c.模型简单,模型预测效率高
d.不太容易显式的用数学表达式表达,不可微.
前三条可以理解为决策树的有点,最后一条因为决策树的表现形式原因,天生就不容易使用数学表达式来描述,可以理解为缺点.
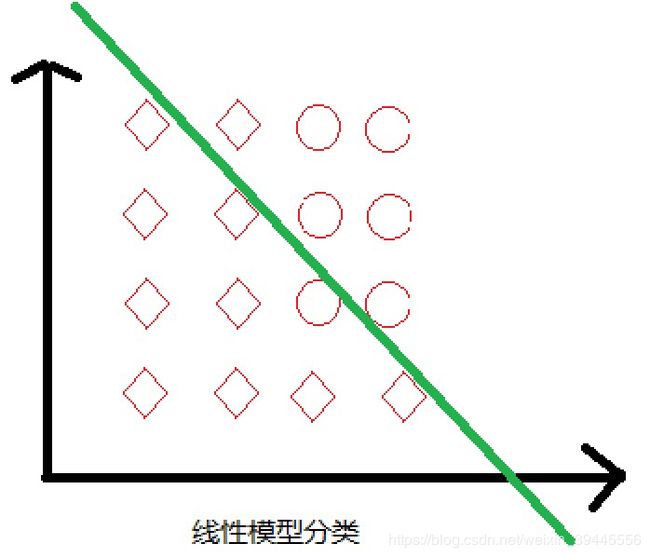
我们知道使用线性模型进行分类,比如逻辑回归是不容易做非线性分类问题的.比如入图2上的数据集无法使用线性模型完美处理,使用树结构来分类结果却比较好.
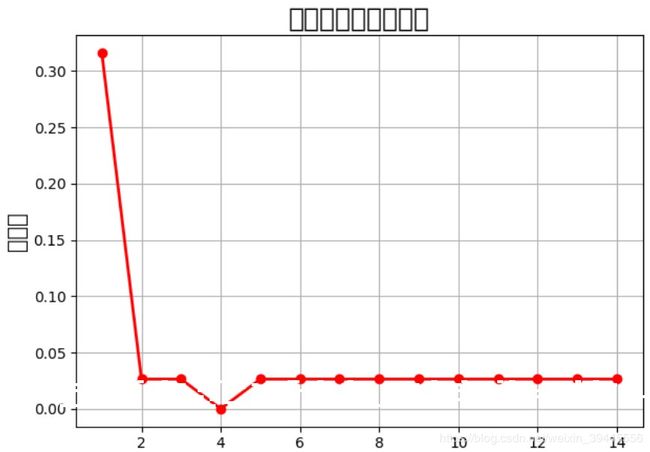
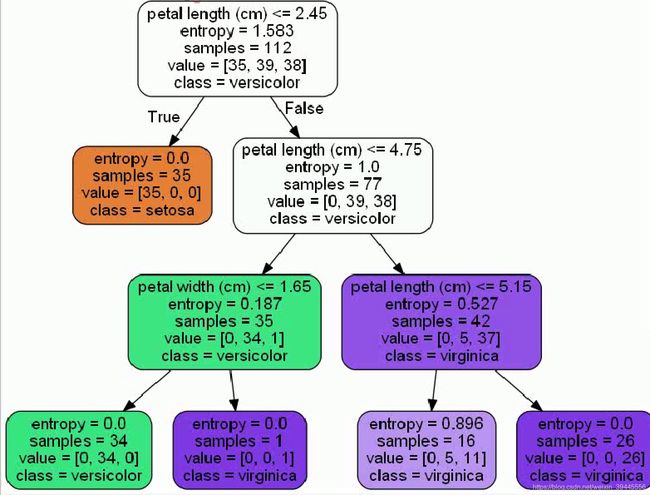
第三张图采用决策树的方法分类,第一次使用x1作为阈值,x>x1的分一类,x 2-生成决策树 机器学习中使用决策树的目标是通过大量数据 ,成一颗非常好的树,用这棵树来预测新来的数据.决策树的生成就是数据不断分裂的递归过程,每一次分裂都尽可能让类别一样的数据在一个子节点上,当子节点所有数据都是一类的时候,停止分裂.我们可以把这个过程理解为一系列的 if else判断..那么如何生成决策树呢. 决策树有四个要素,分别是: 1)-每一个分支节点的分裂条件是什么 2)-每棵树应该分几叉 3)-如何确定最终的叶子节点表达 4)-什么时候停止分裂 我们只需要依次解决这四个问题,就可以顺利完成决策树的生成. 3-确定分裂条件与分支数 常用的分裂条件计算标准有Gini系数,信息增益,信息增益率和MSE,前三者用来判断数据的纯度,也就是用来判断数据一个子节点上的数据都是一类数据的标准,而MSE是在做回归问题的时候使用.没错,决策树可以用来做回归.不管是使用哪种评判标准,当我们进行完一次分裂的时候,都希望每个子节点分到的数据纯度越来越高,因为我们最终是希望将所有属于一类的数据都分到一起,纯度高代表的就是一个子节点上属于同一类数据的占比高. Gini系数: 计算基尼系数的公式为 公式一中讲的是计算单个节点的基尼系数,那如果我们将根节点的数据分到了两个子节点上,如果想评判这次分裂的好与坏,就需要用着两个子节点基尼系数的和来同单节点的基尼系数做比较.多个节点的基尼系数如何计算呢?公式如下: 公式二中,D代表总体数据的数量,D1代表第一类数据的数量.可见,多个节点的基尼系数计算就是该节点单个节点的基尼系数乘以其在总体数据量中的占比.然后将所有子节点的基尼系数求和即可. 假设数据集是一个又10个维度的矩阵,请动脑思考一下,每次计算基尼系数,可以使用几个维度?每次计算基尼系数我们只能选其中的一个维度来计算.那如果我把分别以这10个维度中所有数据作为分裂条件的基尼系数都算出来,选出基尼系数最小的一次结果,是不是就选出了这一次分裂最能让数据变纯的值.实际上决策树就是这样做的.它会遍历维度进行分裂,选择表现最好的训练数据值作为分裂条件.当然在底层,算法在找到最优的分裂条件是会在每个维度中做一些类似于二分查找的优化,不会完完全全的计算所有数据的Gini系数. 到此,我们就通过使用第一种方法基尼系数,解决了生成决策树的第一个问题:分裂条件的选择.我们只需要选择让决策树遍历所有数据去计算基尼系数即可. 使用基尼系数作为分裂评判条件的树叫做CART(Classification And Regression Tree)树,也是最常用的一种树.在CART树中,我们规定,每次分裂只分两支,也就是说每次分类我们都只做二分类任务.而多分类可以用多层的二分类来表达.所以,生成决策树的第二个问题也解决了,在CART树中,固定分2支.同样固定分两支的还有ID3,ID3默认使用的分裂条件判断标准是信息增益. 信息增益:信息增益中首先引入了信息和信息熵的概念,信息的计算公式为: 信息熵的计算公式为: 信息增益率:最后一个跟数据纯度相关的纯度评判标准是信息增益率,看到这个名字就知道它一定跟信息增益有关.信息增益率的计算公式为: 4-叶子节点如何表达 当我们将所有的数据集根据Gini系数也好其他的纯度评判条件也好分成了若干类,当分到不能再分的时候,此时的节点就是我们要的叶子节点.但是每个叶子节点并不都是熵为0,叶子节点的表达形式就是以该节点占比较大的数据的标签为结果的.假如做一个健康预测,我们拿到的数据就是一个人的身高体重,通过决策树最终将体重>200kg的人分到了一个节点.此时我们需要统计所有体重>200kg的人有多少健康(统计lable值,决策树是有监督机器学习),有多少不健康.取占比多的作为叶子节点的表达形式. 假设有10个人是健康的,90个人是不健康的,下一次再有数据通过我们生成的树被分到了这个叶子节点,那就判定这个人不健康. CART回归树 决策树是如何使用MSE来分裂的呢?使用MSE分裂的树的代表有CART回归.我们知道MSE = (y_hat - yi)^2 (注:y_hat就是y上边有个尖角号的那个y的期望值) ,y_hat在线性模型中 = wTx,此时我们没有w,y_hat其实等于这个节点上所有yi的平均值.MSE = (y_mean - yi)^2.可以想象一下,CART回归树在分裂时,y_mean和yi越接近的,MSE就越小,也就越容易分到一起.y_mean就是这个节点上所有yi的平均数,所以节点上数据yi越相近,则y_mean和yi的差值越小.所以最终CART回归树会将yi相近的样本分到一个叶子节点,这个叶子节点的表达就用y_mean来表示.而既然是CART回归树,每次分支的数量也固定是两支. 5-什么时候停止分裂 刚刚讲到,每个叶子节点的熵不都是为0的,可加入让我们无限制的一直分类下去,是可以做到每个样本分作一类的,此时的熵就是0,聪明的人已经想到的,此时的状况就已经是过拟合了,这也是决策树最大的弊端.如果不想让决策树过拟合,有两个办法: a-预剪枝 在算法中提前设置超参数,当决策树分裂出的子节点达到这个数的时候就停止分裂,最终的子节点作为叶子节点.可设置的超参数有:叶子节点中最少要有多少数据,少于这个数据就不分了;决策树一共可以分多少层,达到层数停止分裂;决策树子节点的数量等等.缺点是容易造成欠拟合. b-后剪枝 后剪枝是对决策树不做限制,生成一个完全生长的过拟合的树,使用现有的测试集一点一点的减掉叶子节点暴露新的叶子节点,然后迭代测试.后剪枝的算法包括Reduced-Error Pruning (REP,错误率降低剪枝)和Pessimistic Error Pruning (PEP,悲观剪枝). 后剪枝需要用训练集不断的实验如何保留分支,从下到上一点一点减掉分支,所以花费时间很多. 6-代码实现 一下为使用决策树对鸢尾花数据集分类的代码,在最后把决策树层数与预测准确率做了对比: 决策树层数和准确率对比图,横轴为层数,纵轴为误差: 决策树分支过程如下: 以上为决策树的学习.感谢您的阅读.欢迎大佬帮忙勘误,在此提前感谢. 下一篇:随机森林(Random Forest)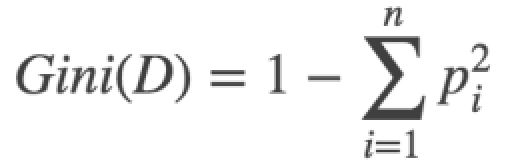 (公式一),公式中
(公式一),公式中![]() 为P所属类别的数据在总体数据中的占比.加入一共有10条数据,我们要把它分成两类.如果每一类数据各有5条,则基尼系数的计算就是
为P所属类别的数据在总体数据中的占比.加入一共有10条数据,我们要把它分成两类.如果每一类数据各有5条,则基尼系数的计算就是![]() .10条数据每一类占5条是二分类时数据最不纯的情况,所以基尼系数分类最差的情况就是等于0.5.如果第一类数据有1条,第二类数据有9条,根据Gini系数的计算公式,
.10条数据每一类占5条是二分类时数据最不纯的情况,所以基尼系数分类最差的情况就是等于0.5.如果第一类数据有1条,第二类数据有9条,根据Gini系数的计算公式,![]() .由此可见,数据越纯,基尼系数越小.
.由此可见,数据越纯,基尼系数越小.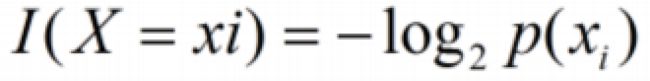 ,公式中P(x)为x在所有样本中出现的概率,如果数据集中重复的样本越多,则该样本的信息越小.
,公式中P(x)为x在所有样本中出现的概率,如果数据集中重复的样本越多,则该样本的信息越小. ,样本出现的概率与该样本的信息相乘,求得所有样本的概率与该样本的信息相乘的和取负号就是信息熵.信息熵表述了:一个数据集可以被完整传输的平均码长的期望.数据越纯,则数据的信息熵越小.信息增益的定义是数据分裂前的信息熵减去分裂后的信息熵.一个分裂导致的信息增益越大,则代表这次分裂提升的纯度越高.
,样本出现的概率与该样本的信息相乘,求得所有样本的概率与该样本的信息相乘的和取负号就是信息熵.信息熵表述了:一个数据集可以被完整传输的平均码长的期望.数据越纯,则数据的信息熵越小.信息增益的定义是数据分裂前的信息熵减去分裂后的信息熵.一个分裂导致的信息增益越大,则代表这次分裂提升的纯度越高.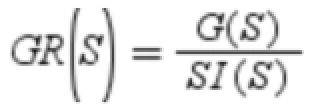 ,其中G(S)就是我们刚刚讲的信息增益,而
,其中G(S)就是我们刚刚讲的信息增益,而 ,SI(S)是类别本身的熵.采用信息增益率进行分裂的算法是C4.5,同ID3不同,C4.5并没有一次只能分2支的限制,它可以一步就将数据从熵最大分类到熵为0.但是当我们对C4.5不做限制时,算法又刚好选择了序号这一列作为分裂条件,数据就完全的过拟合了.所以在信息增益的基础上除以一个惩罚项SI(S)来抑制这种情况.通过信息增益率的计算公式,算法会自动的决定出分几支最合适.
,SI(S)是类别本身的熵.采用信息增益率进行分裂的算法是C4.5,同ID3不同,C4.5并没有一次只能分2支的限制,它可以一步就将数据从熵最大分类到熵为0.但是当我们对C4.5不做限制时,算法又刚好选择了序号这一列作为分裂条件,数据就完全的过拟合了.所以在信息增益的基础上除以一个惩罚项SI(S)来抑制这种情况.通过信息增益率的计算公式,算法会自动的决定出分几支最合适.import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
import matplotlib as mpl
#读取iris数据集
iris = load_iris()
# 读取数据集
data = pd.DataFrame(iris.data)
data.columns = iris.feature_names
data['Species'] = load_iris().target
#取数据帧的前四列(所有行)也就是X
x = data.iloc[:, :4] # 花萼长度和宽度
#取数据帧的最后一列(所有行)也就y
y = data.iloc[:, -1]
#训练集和测试集的划分
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.75, random_state=42)
tree_clf = DecisionTreeClassifier(max_depth=6, criterion='entropy')
tree_clf.fit(x_train, y_train)
y_test_hat = tree_clf.predict(x_test)
print("acc score:", accuracy_score(y_test, y_test_hat))
#生成一个数组
depth = np.arange(1, 15)
err_list = []
for d in depth:
clf = DecisionTreeClassifier(criterion='gini', max_depth=d)
clf.fit(x_train, y_train)
y_test_hat = clf.predict(x_test)
result = (y_test_hat == y_test)
# 生成一个长度为验证集数量的数组,每一个元素是yhat和y是否相等的结果,
print(list(result))
if d == 1:
print(result)
#生成错误率
err = 1 - np.mean(result)
print(100 * err)
err_list.append(err)
print(d, ' 错误率:%.2f%%' % (100 * err))
plt.figure(facecolor='w')
plt.plot(depth, err_list, 'ro-', lw=2)
plt.xlabel('决策树深度', fontsize=15)
plt.ylabel('错误率', fontsize=15)
plt.title('决策树深度和过拟合', fontsize=18)
plt.grid(True)
plt.show()
# tree_reg = DecisionTreeRegressor(max_depth=2)
# tree_reg.fit(X, y)