Python高级--朴素贝叶斯
一、贝叶斯
1)贝叶斯原理
![]()
公式中,事件Bi的概率为P(Bi),事件Bi已发生条件下事件A的概率为P(A│Bi),事件A发生条件下事件Bi的概率为P(Bi│A)。
2)贝叶斯解决的问题
实例一:
我们想预测北京的冬天某一天下雪,当天堵车的概率是多少P(B|A)
A是下雪P(A) = 0.1
B是堵车P(B) = 0.8
如果某一天堵车,下雪的概率是 0.1 P(A|B) = 0.1
P(B|A) = 0.8*0.1/0.1 = 0.8
可以看出下雪天堵车的概率为0.8
实例二:
一座别墅在过去的 20 年里一共发生过 2 次被盗,
别墅的主人有一条狗,狗平均每周晚上叫 3 次,
在盗贼入侵时狗叫的概率被估计为 0.9,
问题是:在狗叫的时候发生入侵的概率是多少?
A 事件为狗在晚上叫 P(A) = 3/7
B 为盗贼入侵 P(B) = 2 / (20*365)
P(A|B) = 0.9
狗叫了 发生 盗贼 入侵 的 概率 P(B|A) = P(A|B)*P(B)/P(A)
(9/10)*(2/(20*365))/(3/7) = 0.0005753424657534247
可以预测到狗叫了,盗贼入侵的概率
二、朴素贝叶斯原理
1)朴素贝叶斯与贝叶斯的关系
朴素贝叶斯是对贝叶斯的一种简化
通过引入独立性假设,从而大大降低了计算量
朴素的概念:独立性假设,假设各个特征之间是独立不相关的
独立性假设:
一直小狗是母狗与这只狗是一个泰迪 这两个假设就相互独立
非独立性假设:
库里是篮球运动员与 库里的投篮很准
这两个特征有关系,因为库里是篮球运动员,训练很刻苦,多以投篮很准。
2)实际中主要用于自然语言处理
三、3种贝叶斯模型
1)导包、获取数据
from sklearn.naive_bayes import GaussianNB,MultinomialNB,BernoulliNB
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt取前两列绘图查看
data = iris.data[:,:2] # 所有行 前两列 特征值
target = iris.target # 目标值
plt.scatter(data[:,0],data[:,1],c=target)2)高斯分布朴素贝叶斯
高斯朴素贝叶斯 一般是用来对 符合正态分布的 数据 进行分类的
这类数据 的分布 一般是 中间多 周围少
1、调用构造函数 获取模型 并训练
gnb = GaussianNB()
gnb.fit(data,target)2、测试数据
x = np.linspace(data[:,0].min(),data[:,0].max(),100)
y = np.linspace(data[:,1].min(),data[:,1].max(),100)
xx,yy = np.meshgrid(x,y)
X_test = np.c_[xx.flatten(),yy.flatten()]3、模型预测
y_ =gnb.predict(X_test)
4、预测数据绘图
# 创建指定点的颜色
from matplotlib.colors import ListedColormap
cmap1 =ListedColormap(['r','g','b'])
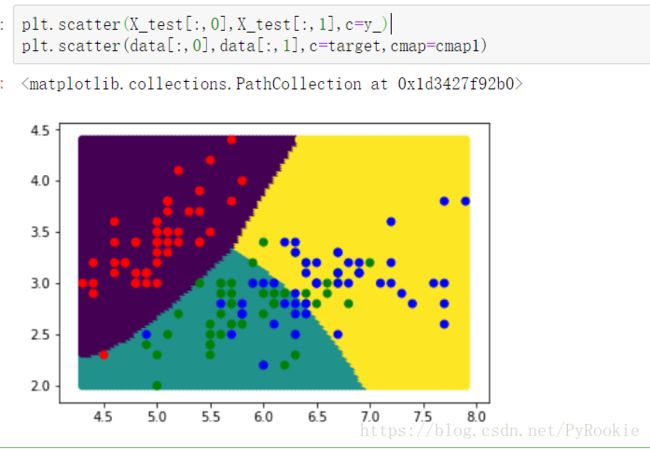
plt.scatter(X_test[:,0],X_test[:,1],c=y_)
plt.scatter(data[:,0],data[:,1],c=target,cmap=cmap1)5、简单看分类的准确率
取所有特征,并且要 把 数据集 分成 训练集 和 测试集
#自带的可以打乱顺序并将数据集分成训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(data,target,test_size=0.2)#获取模型并训练
gnb = GaussianNB()
gnb.fit(X_train,y_train)#获取准确率
gnb.score(X_test,y_test)
0.96666666666666673)多项式分布朴素贝叶斯
适用于文本数据(特征表示的是次数,例如某个词语的出现次数)
4)伯努利分布朴素贝叶斯
适用于伯努利分布,也适用于文本数据(此时特征表示的是是否出现,例如某个词语的出现为1,不出现为0)
绝大多数情况下表现不如多项式分布,但有的时候伯努利分布表现得要比多项式分布要好,尤其是对于小数量级的文本数据
四、文本分类实战
对短信进行二分类,数据为SMSSpamCollection
1)加载数据
import pandas as pd
from pandas import Series,DataFrame# spam是垃圾邮件 ham是正常邮件
df = pd.read_table('./data/SMSSpamCollection.tsv',header=None)
df # 最开始的一列不是列索引 header=None数据处理
data = df[1] # 内容 (特征值)
target = df[0] # 目标值2)使用机器学习模型 对 邮件进行分类
1、获取模型
mnb = MultinomialNB()
bnb = BernoulliNB()2、训练模型
注意: 不能直接用文本内容去训练机器学习模型
mnb.fit(data,target) 机器学习模型 肯定无法直接对 文本信息进行学习
我们需要对文本信息 进行特征值抽取
最后是使用文本的特征值 对 机器学习模型 进行训练
3、对训练集处理
from sklearn.feature_extraction.text import TfidfVectorizer
'''
feature_extraction 特征抽取
text 文本特征的抽取
Tfidf Vectorizer 词频逆文档频率
Tfidf tf idf
tf term frequency 词频 词语在文章中出现的频率
idf inverse document frequency 逆文档频率
Tfidf 其实就是 某个词在当前文章中出现的频率/这个词语在所有文章中出现的频率
'''4、创建 词频逆文档频率 抽取文章特征
tf = TfidfVectorizer() # 用来抽取文章的特征
tf.fit(data) # 对所有内容进行学习
data_tf = tf.transform(data) #对学习的内容进行特征抽取5、训练数据
使用 抽取特征后的 数据 对机器学习模型进行 训练了
mnb.fit(data_tf,target)
bnb.fit(data_tf,target)6、测试数据
X_test= [
'I love you',
'Please call our customer service as you have WON £1000 cash prize!',
'Dear customer, welcome to the UAE and thank you for choosing du',
'Congratulations, you won a prize',
'We will reply to your inquiry within the next two business days.',
'this is a spam',
'prize and cash',
'Sign up to 3Plus for a chance to win your dream trip for two'
]对测试数据进行处理
这里可以直接传入一个列表 列表中是各个文档内容
# 对 测试数据进行 处理
X_test_tf = tf.transform(X_test)7、测试结果
预测的时候 也是先要把 测试文档的特征抽取出来 然后 让机器学习模型去预测
数据量大的情况下 肯定是 多项式朴素贝叶斯更好 (数据量小的情况下 有可能伯努利效果更好 只是可能)
mnb.predict(X_test_tf)
array(['ham', 'spam', 'ham', 'spam', 'ham', 'ham', 'spam', 'ham'],
dtype=') bnb.predict(X_test_tf)
array(['ham', 'spam', 'ham', 'ham', 'ham', 'ham', 'ham', 'ham'],
dtype=') 五、垃圾邮件分类
对email进行二分类,两种邮件分别在ham和spam目录下
1)数据读取
1、先尝试读取一个
file_path = './data/email/ham/1.txt'
open(file_path).read()
'Hi Peter,\n\nWith Jose out of town, do you want to\nmeet once in a while to keep things\ngoing and do some interesting stuff?\n\nLet me know\nEugene'2、将25个文件都读取
读取ham中的所有文件
ham = []
# ham 目录下的25个都读取
for i in range(1,26):
file_path = './data/email/ham/%d.txt'%(i)
# print(file_path)
data = open(file_path,encoding='gbk',errors='ignore').read()
ham.append([data,'ham'])
df1 = DataFrame(ham)读取spam 中的所有文件
spam = []
# spam 目录下的25个都读取
for i in range(1,26):
file_path = './data/email/spam/%d.txt'%(i)
# print(file_path)
data = open(file_path,encoding='gbk',errors='ignore').read()
spam.append([data,'spam'])
df2 = DataFrame(spam)将两个DataFrame合并起来
df = pd.concat([df1,df2])2)数据处理
1、先对数据整体 进行 抽取特征
tf = TfidfVectorizer() # 调用构造函数 获取模型
tf.fit(df[0]) #使用模型对数据进行获取
tf.transform(df[0]) # 对数据进行转换训练个转换同时进行
data_tf = tf.fit_transform(df[0]) # 如果 训练 和 转换 用的是一个数据集 直接使用fit_transform即可3)分离训练数据和测试数据
X_train, X_test, y_train, y_test = train_test_split(data_tf,df[1],test_size=0.25)
# 特征值是 data_tf 也就是 抽取了特征后的文本信息
# 目标值是 df里1那一列 也就是 标记的 ham和spam
# test_size是切分的比列4)使用机器学习模型训练
多项式分布朴素贝叶斯
mnb = MultinomialNB() #获取模型
mnb.fit(X_train,y_train) #训练模型
mnb.score(X_test,y_test) # 查看准确立率
0.9230769230769231伯努利分布朴素贝叶斯
bnb = BernoulliNB()
bnb.fit(X_train,y_train)
bnb.score(X_test,y_test)
0.9230769230769231