0x00 基本算法 --- 递推与递归

AcWing 92. 递归实现指数型枚举

定义递归，我认为最重要的是确定递归的出口，在这道题中的出口就是当递归函数输入的数等于n时，代表着该分支已经遍历完所有的n个数。state代表着某个数是否被选中。
递归函数中需要确定分支，这里的每个数都有两种可能，一种是未被选中，一种是被选中，如果被选中则state | 1 << u，代表state的第u位置为1, 在最后输出时, 通过1 & state >> i，可以确定在递归过程中，哪些数被选中。

def dfs(u, state):
    if u == n:
        for i in range(n):
            # 是否选到这个数
            if 1 & state >> i:
                print(i + 1, end='')
        print()
        return

    # 不选这个数
    dfs(u + 1, state)
    # 选这个数
    dfs(u + 1, state | 1 << u)


if __name__ == '__main__':
    n = int(input())
    dfs(0, 0)

AcWing 93. 递归实现组合型枚举

本道题的输出多了一个限制sum，我们选择的数需要等于sum，所以在递归函数中还需要输入sum。
递归的出口这里有两个，第一个为sum + n - u < m， 这里是进行剪枝的操作，意思是如果当前选中的数加上剩下的所有数的个数都小于给定选定数字的数量的话，则直接返回。第二个则当sum等于m时，就是我们需要的答案。
在每个数的分支中，这里在选中这个数的同时，还需要将sum进行加1。

n = 5
m = 3


def dfs(u, sum, state):
    # 加上剩下的所有数都不能满足条件，直接跳出
    if sum + n - u < m:
        return

    if sum == m:
        for i in range(n):
            # 是否选到这个数
            if 1 & state >> i:
                print(i + 1, end='')
        print()
        return

    # 选这个数
    dfs(u + 1, sum + 1, state | 1 << u)
    # 不选这个数
    dfs(u + 1, sum, state)


if __name__ == '__main__':
    # 总数，选了几个数，选择策略
    dfs(0, 0, 0)

AcWing 94. 递归实现排列型枚举

这题是全排列的问题，首先还是定义递归的出口，这里就是当sum等于n时，代表每个数字我们都已经选中了。好像跟上一题有一些相似，但是区别在于选数的时候，上一题的选数时，但递归选中了3后，递归函数不会再递归到小于3的数，即不可能出现132这样的序列。所以两道题的区别在于，本道题需要每个递归都要从头开始，即从0到n。这里需要一个used列表，来保存哪些数字被使用过，用path存储使用的数字。
重要的一点的时在循环中，当选中的数进入的递归循环结束后，需要将还原现场，便是将该数的uesd:True改为False，以便于在其他比它大的数在遍历时，可以使用到。同时将在path中pop出该数。

n = 3
res = []
path = []
used = [False] * n


def dfs(sum, path):
    if sum == n:
        res.append(path.copy())
        return

    for i in range(n):
        # 没有使用过这个数
        if not used[i]:
            used[i] = True
            path.append(i + 1)
            dfs(sum+1, path)
            used[i] = False
            path.pop()


if __name__ == '__main__':
    dfs(0, path)
    print(res)

AcWing 95. 费解的开关

首先，确定一下思路。对不起，我没有思路
先简化一下题目，输入的为5*5的一个“地图”，在经过少于等于6次的操作后，需要将所有数字都变为1。每次按下一个位置，这个位置与上下左右四个方向的数字都要改变，从1->0或0->1。是不是一头雾水，是不是不知道怎么下手，这就对了。
我们重点看按下一个位置后，这个位置与其上下左右都会改变。我们希望一步一步解决问题，即当某个位置已经被我们改变为1后，这个位置我们不希望再被改变。所以我们需要有规律的去操作这些数。废话连篇，mdzz
即我们假设第一行不变，我们操作第二行，在操作第二行时有一个条件，我们在第二行按下的位置对应的第一行的位置为0，这样我们才能按。这里简单模拟一下，比如第一行是101，第二行时001，这样第一行的第二个为0，所以我们需要按下第二行的第二个位置，这样第一行的第二个位置都变为了0。所以当我们遍历完第二行，第一行的所有数都变为1，以此类推，直到最后一行被操作结束。最后验证最后一行的数字是否都为1，并且变换的次数小于等于6，输出操作次数，否则返回-1。
对了，还有最重要的一步是对第一行的操作，一共有32种操作，每个位置都有两种操作，2^5=32，所以循环32次，每次都进行上述操作，选出操作步数最小的方法。

# 1. 枚举第一行改变的状态
# 2. 根据第一行的状态改变第二行的状态
# 3. 以此类推
import copy
def to_one_char(s):
    l = []
    for j in s:
        l.append(j)
    return l


# 点击开关
def turn(i, j, temp):
    dx = [0, 1, 0, -1, 0]
    dy = [0, 0, 1, 0, -1]

    for pos in range(5):
        new_x = i + dx[pos]
        new_y = j + dy[pos]
        if 0 <= new_x < len(temp) and 0 <= new_y < len(temp[0]):
            temp[new_x][new_y] ^= 1


if __name__ == '__main__':
    n = int(input())
    for i in range(n):
        temp = []
        res = 0
        count = 0
        min_res = 10000000000
        for j in range(5):
            s = input()
            temp.append(list(map(int,to_one_char(s))))
        backup = copy.deepcopy(temp)
        # print(backup)
        # 空格
        if i < n - 1:
            s = input()
        # 循环遍历第一行的操作，共有2^5
        for i in range(1 << 5):
            for j in range(5):
                if i & 1 << j:
                    res += 1
                    turn(0, j, temp)
            # 根据第一行操作剩下四行
            for i in range(1, 5):
                for j in range(5):
                    # 判断当前位置的上一个格子的状态
                    if temp[i-1][j] == 0:
                        res += 1
                        turn(i, j, temp)
            # 判断最后一行的灯是否全亮
            for j in range(5):
                if temp[4][j] == 1:
                    count += 1
            if count == 5 and res <= 6:
                min_res = min(res, min_res)
            temp = copy.deepcopy(backup)
            res = 0
            count = 0
        if min_res == 10000000000:
            print(-1)
        else:
            print(min_res)
        temp.clear()

AcWing 96. 奇怪的汉诺塔

这里d列表为3个塔的值，下面注释挺详细的。
重要的是f列表4个塔的值，这里为什么会有一个for j in rang(i)的循环。这里应该是在四个塔时，我们可以选择选择移走前j圆盘，但是j多少是不确定的，所以需要进行循环。在需要移走总数i个圆盘时，判断先移走多少个(j)圆盘时，总操作数最少。有点绕口，多看几遍就明白了。

if __name__ == '__main__':
    # 首先存储三个汉诺塔的情况
    d = [0] * 15
    f = [10000] * 15
    f[0] = 0
    for i in range(1, 13):
        # d[i-1] + 1 + d[i-1]
        # 1. 首先将前i个圆盘移动到第三个塔上，总共操作次数为d[i-1]
        # 2. 然后将第i个圆盘移动到第二个塔上, 操作次数为1
        # 3. 最后将i-1个圆盘移动到第二个塔上，操作次数为d[i-1]
        d[i] = 1 + d[i-1] * 2

    # 四个塔的情况
    for i in range(1, 15):
        # 判断在四个塔的情况前，先移走前j塔时，最少使用步数
        for j in range(i):
            f[i] = min(f[i], f[j] * 2 + d[i-j])
    print(d)
    print(f)

AcWing 97. 约数之和

这道题的核心是：任何合数都可以表示成质数的指数幂乘积的形式，如果将质数从小到大排列，那么这个分解式唯一。

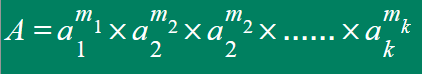
举个例子: 108 = 2^2 + 3^3
P为正约数的个数，(2+1) * (3 + 1) = 12，因为2^2可以有三种选择, 2^0, 2^1, 2^2 ，3同理。我们再把每个正约数列出来，看是否是12个，[1, 2, 4]×[1, 3, 9, 27] (这里是笛卡尔积) = [1, 3, 9, 27, 2, 6, 18, 54, 4, 12, 36, 108] 正好是12个。
这道题求的是A^B,其中我们只需要求出A的正约数即可，因为根据幂的计算规则(2 ^2 * 3^2) ^ 2可以直接转换成2^4 * 3 ^ 4。
以108为例，当我们要计算所有约数之和的时候， 只需要把[1, 2, 4]的和乘上[1, 3, 9, 27]的和。
再举个例子说明为什么，假设这两个列表为[1,2]与[1,3]，则笛卡尔积为[1,3,2,6]的和为12，我们展开公式的话为:1×1+1×3+2×1+2×3 = 1×(1+3)+2×(1+3)=(1+2)×(1+3)=12。
接下来就是如何通过递归来计算每个质数幂的和。
这一块就是编写get_sum(a, k)函数，即计算a的k次方中所有约数的和。

首先我们需要确定k是奇数还是偶数，因为我们使用递归，需要不断的减小问题集。因为要减半，所以k的奇偶数会影响递归的子集。
再举例子，我们先假设k为基数。
S = a^0 + a^1 + a^2 + a^3，k = 3
这样我们正好可以将式子左右平分。
S = (a^0 + a^1) + (a^2 + a^3) = (a^ 0+a^1) + a ^ 2(a ^0 + a^1) = (1 + a ^2)(a ^0 + a^ 1)
所以当k = 3时，我们递归的子集就写好了(1 + a^(k // 2 + 1)) * get_sum(a, k// 2)
然后k为偶数时
S = a^0 + a^1 + a^2 + a^3+a ^4，k = 4
这里有一个技巧，我们不直接计算这个式子而是将这个式子改为 a × (a^0 + a^1 + a^2 + a^3) + 1，这样我们就可以把偶数k的计算转变为基数k的计算。
接下来就剩下简单的写代码部分啦

mod = 9901


# 快速幂
def qmi(a, k):
    res = 1
    while k:
        if k & 1:
            res = res * a % mod
        a *= a
        k >>= 1
    return res


def get_sum(a, k):
    # k 为 0, 返回1
    if k == 0:
        return 1
    # 若k为偶数
    if k % 2 == 0:
        return a % mod * get_sum(a, k - 1) % mod + 1
    # 若k为奇数
    return (1 + qmi(a, k // 2 + 1)) % mod * get_sum(a, k//2) % mod


if __name__ == '__main__':
    A, B = map(int, input().split())
    # A^B，可以先算A的质因数，再算次方中乘上B
    res = 1
    # 寻找质因数
    for i in range(2, A+1):
        s = 0
        if A % i == 0:
            s += 1
            A //= i
        if s :
            res = res * get_sum(i, s * B) % mod
    if not A:
        res = 0
    print(res)

AcWing 98. 分形之城

代码可以AC，但是有些坐标转换不是很明白，等我问清楚后，会补上剩下的解释。

这道题是真的简单，我也就用了几个小时，还弄不懂坐标变换而已。
先观察每一级的城市与其下一级城市的区别，我们可以发现N-1级的城市可以通过旋转平移等操作，组成N级城市。然后本题的重点就是在理解坐标旋转上。

我们不看三级城市，三级城市有点复杂。不是因为我看不懂
我们先从简单的开始看二级城市的右上角与右下角的四个城市，这里需要注意的是我们一级城市的1234,需要与二级城市的4567,891011城市的需要一一对应才行，就是1要对应4,2要对应5以此类推，并且线条的顺序也要对应上。所以在当从一级城市到二级城市的右上角对应的城市时，只需要把一级城市向右平移，二级城市的右下角同理，先向右平移，再向下平移。
不懂的话还是一边看代码一边看解释，比较好理解一点。
这里解释两个变量len与cnt,len为n级城市边长的一半，假设一级城市正方形边长为2，则len为1，二级城市边长为4，则len为2。
cnt为N-1级城市中房屋的数量。

import math


# 此处计算时，单位为1
def get_pos(n, m):
    """
    :param n: 城市等级
    :param m: 城市编号
    :return: 城市编号坐标
    """

    # 出口：0级城市
    if n == 0:
        return 0, 0
    # n级城市边长的一半
    len = 1 << (n - 1)
    # 子问题中点的数量
    cnt = 1 << (2 * n - 2)
    pos = get_pos(n - 1, m % cnt)
    x, y = pos[0], pos[1]
    # z为位置
    # 0: 左上角, 1: 右上角, 2: 右下角, 3: 左下角
    z = m // cnt
    if z == 0:
        return y, x
    if z == 1:
        return x, y + len
    if z == 2:
        return x + len, y + len
    return len * 2 - 1 - y, len - 1 - x


if __name__ == '__main__':
    t = int(input())
    while t:
        n, a, b = input().split()
        print(n, a, b)
        # 首先计算出a,b两点左边
        ax, ay = get_pos(int(n), int(a) - 1)
        bx, by = get_pos(int(n), int(b) - 1)

        # 计算欧式距离
        x = ax - bx
        y = ay - by
        distance = math.sqrt(x ** 2 + y ** 2) * 10
        t -= 1
        print(round(distance))

最后十分感谢yxc学长的悉心教导。
Acwing入口
yxc学长B站入口