字典树Trie学习笔记
一个简单的问题
问题:有 n n n个由小写字母组成的字符串( n ≤ 1 0 5 n\le 10^5 n≤105,字符串长度 L ≤ 20 L\le 20 L≤20)。有 Q Q Q组询问( Q ≤ 1 0 5 Q\le10^5 Q≤105),每次给出一个字符串,你需要回答这个字符串在给出的 n n n个字符串中是否出现。
方法一:暴力,每个询问和前面大莉比较,时间复杂度 O ( Q n L ) O(QnL) O(QnL)。
方法二:把 n n n个字符串存入map中,每个询问在map中查询。不太清楚map复杂度怎么算,目测总时间复杂度 O ( L n l o g n + L Q l o g n ) O(Lnlogn+LQlogn) O(Lnlogn+LQlogn)。
方法三:蛤希,时间复杂度 O ( L n + L Q ) O(Ln+LQ) O(Ln+LQ),但可能会有蛤希冲突。
方法四:Trie。
Trie树基本内容
建立和查询方法
在Trie树中,我们用边来表示每个字符,点表示字符串结束的位置。
让每个点所对应的字符串为根节点到这个点的路径所对应的字符按顺序连接得到的字符串。
举个例子:现在有四个字符串ypy,ygy,yxc,mhy。那么珂以根据规则建立Trie树:
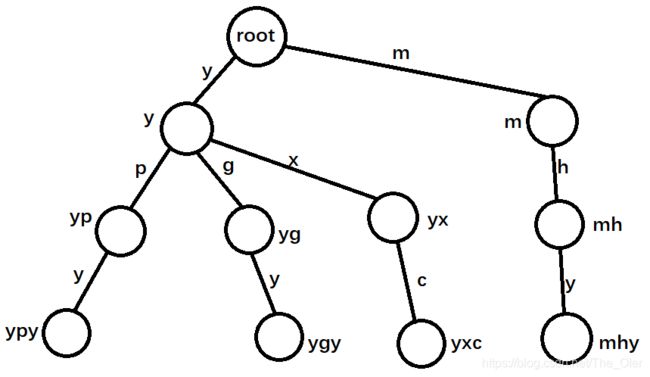
建立了trie树,便珂以在trie树上维护信息。例题中,珂以在字符串出现的位置打上标记:

每次询问时,按照字符串访问每个字符所对的边,看最后到达的节点是否有标记即珂。
毒瘤代码实现
实现时使用动态开点。
变量定义&插入代码:
#define re register int
int tot=1;
struct node {
int ch[27];
bool flag;
} w[Size*21];
void insert(char *str) {
int len=strlen(str),rt=1;
for(re i=0; i<len; i++) {
int p=str[i]-'a';
rt=w[rt].ch[p]?w[rt].ch[p]:w[rt].ch[p]=++tot; //实测insert中用三目运算符比if快10%左右
}
w[rt].flag=true;
}
询问代码:
bool query(char *str) {
int len=strlen(str),rt=1;
for(re i=0; i<len; i++) {
rt=w[rt].ch[str[i]-'a'];
if(!rt) return false; //rt=0说明没有这样的字符串,直接剪枝
}
return w[rt].flag;
}
Trie题目
例题一
UVA11362 Phone List & SP4033 Phone List & poj3630 Phone List
给定 n n n 个长度不超过 10 10 10 的数字串,问其中是否存在两个数字串 S , T S,T S,T,使得 S S S 是 T T T 的前缀。
把所有数字串存入Trie中,Trie每个节点保存子树内有多少个节点对应的字符串存在(即每个节点保存有多少个字符串的前缀为这个节点对应字符串的),记为 s u m sum sum。
每个节点再保存是否存在这个节点对应的字符串,记为 f l a g flag flag。
那么若这个节点的字符串是其他字符串的前缀,当且仅当 f l a g flag flag & & \&\& && s u m > 1 sum>1 sum>1。
所以dfs一遍即珂。
代码略。
例题二
洛谷P5768 [CQOI2016]路由表 LOJ #2046 [CQOI2016]路由表
题目大意:路由表中珂以存储IP地址,称为表项。每个表项有一个掩码长度。
对于一个给定的IP(目的地址),路由表会将这个IP与所有表项比较,比较时只会比较前掩码长度位。(掩码长度指的是这个表项的掩码长度)
在所有能匹配的掩码中,路由表会选出一个掩码长度最长的IP,称为表项选择。
起初路由表是空的。要求资瓷两种操作:
1.往路由表中插入一个掩码长度为 l l l的表项
2.给出一个目的地址和两个整数 a , b a,b a,b,输出这个IP在第 a a a次和第 b b b次插入表项之间,表项选择变了多少次
建立Trie与例题一同理(把IP的前 l l l位插入Trie中)。
查询方式:
考虑表项变化的情况,发现表项变化只有可能是掩码长度大于之前的掩码长度,且出现时间比之前的IP晚。
如果出现时间比前面的IP早且掩码长度比前面的IP掩码长度长,则说明前面的IP不会称为表项选择。
因此根据给出的目的地址在Trie中递归,用单调栈记录一个单调递增的时间序列,最后其中时间 > = l >=l >=l且 < = r <=r <=r的就是答案。
毒瘤代码
#include例题三
LOJ #10050 The XOR Largest Pair
给定 n n n个整数 a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1,a2,...,an,取出两个数进行异或运算,得到的结果最大是多少?
扫一遍,每次用 a i a_i ai在Trie树中的异或最大值更新答案,再把 a i a_i ai插入到Trie树中。
a i a_i ai在Trie树中异或最大值求法:让另外一个节点向下搜索,尽量与 a i a_i ai反方向走。显然这样异或是最大的。
代码略。