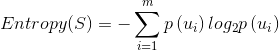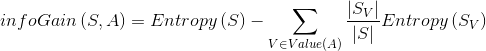【机器学习】分类算法–决策树（ID3/C4.5/CART）

前言

决策树，是工业界常用的数据挖掘模型。其原理是根据一个或多个特征的划分来确定分类，易于理解。和K邻近算法一样，决策树是属于分类、有监督的算法

决策树常用的有ID3算法、C4.5算法和CART算法。ID3算法和C4.5算法都是分类算法，CART算法是回归算法。

我们今天通过一个天气-活动预测的数据来了解这三个算法

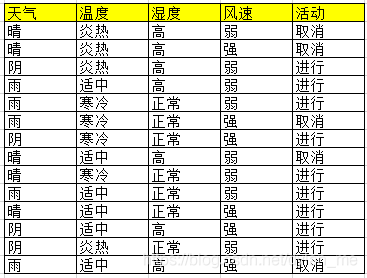
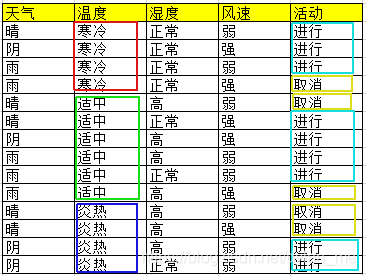
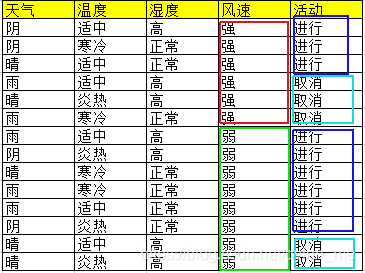
上述数据集有4个属性，属性集合A={ 天气，温度，湿度，风速}， 类别标签有2个，类别集合L={进行，取消}

---

正文

本文要介绍的三种算法在特征选择的方法上存在差异：ID3用信息增益，C4.5用信息增益率，CART用Gini系数。下面先讲讲理论概念，只要掌握了这几个知识点，那么决策树的问题你就懂了一大半了

 

公式及原理

信息熵

   ，  

表示类别在样本中出现的概率， 计算的是所有样本的信息熵。

案例中样本S及每个属性的信息熵计算过程如下：

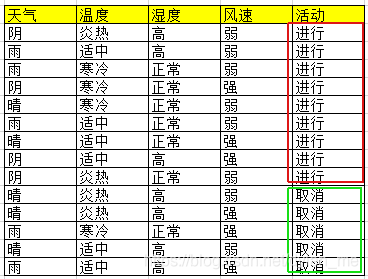
Entropy(S) = -(9/14 * log2(9/14) + 5/14 * log2(5/14)) = 0.940

Entropy(“天气”) = -(5/14 * [3/5 * log2(3/5) +2/5 * log2(2/5)] + 4/14 * [4/4 log2(4/4)] + 5/14 * [3/5 * log2(3/5) +2/5 * log2(2/5)]) = 0.694

Entropy(“温度”) = -(4/14 * [3/4 * log2(3/4) +1/4 * log2(1/4)] + 6/14 * [4/6 log2(4/6)+2/6 * log2(2/6)] + 4/14 * [2/4 * log2(2/4) +2/4 * log2(2/4)]) = 0.911

Entropy(“湿度”) = -(7/14 * [3/7 * log2(3/7) +4/7 * log2(4/7)] + 7/14 * [6/7 log2(6/7)+1/7 * log2(1/7)]) = 0.789

Entropy(“风速”) = -(6/14 * [3/6 * log2(3/6) +3/6 * log2(3/6)] + 8/14 * [6/8 log2(6/8)+2/8 * log2(2/8)]) = 0.892

 

信息增益

其中，表示样本的属性，是属性所有的取值集合。是的其中一个属性值，是中的值为的样例集合。

简而言之，求和公式里表示的就是属性A（也可以说A特征）的信息熵。

从这个公式里可以看出，是在正负样本确定的时候就变成定值了，唯一变化的就是后面求和公式的部分。

，它的值越大，说明分类效果越好，这就是我们选择树节点特征的依据

案例中的信息增益计算过程：

infoGain( S, “天气”) = Entropy(S) - Entropy(“天气”) = 0.940 - 0.694 = 0.246

infoGain( S, “温度”) = Entropy(S) - Entropy(“温度”) = 0.940 - 0.911 = 0.029

infoGain( S, “湿度”) = Entropy(S) - Entropy(“湿度”) = 0.940 - 0.789 = 0.151

infoGain( S, “风速”) = Entropy(S) - Entropy(“风速”) = 0.940 - 0.892 = 0.048

如果这里用的是ID3算法，那么我们就可以选取“天气”作为第一个分裂属性。

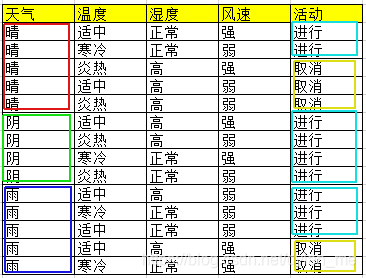
同样，在确定第一个分裂属性后，我们就可以继续计算infoGain( S天气晴, “温度”)、infoGain( S天气晴, “湿度”)、infoGain( S天气晴, “风速”)，为天气晴这个分支继续找分裂属性，直到某个分裂属性的熵为0（也可以说得到了最大的信息增益）。 

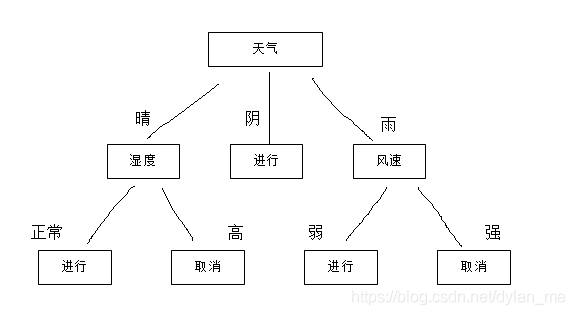
S天气阴、S天气雨也继续找分裂属性。这里，我们就生成了一颗树，我们把它称之为决策树，采用信息增益来选择特征，这就是根据ID3算法生成的决策树。

 

分裂信息

其中S1到Sc是c个值的属性A分割S而形成的c个样例子集。注意分裂信息实际上就是S关于属性A的各值的熵。

SplitInfomation( S, “天气”) =  -( 5/14 * log2(5/14)+ 4/14 *log2(4/14) + 5/14 * log2(5/14) ) = 1.577

SplitInfomation( S, “温度”) =  -( 4/14 * log2(5/14)+ 6/14 *log2(4/14) + 4/14 * log2(5/14) ) = 1.556

SplitInfomation( S, “湿度”) =  -( 7/14 * log2(7/14)+ 7/14 * log2(7/14) ) = 1.0

SplitInfomation( S, “风速”) =  -( 6/14 * log2(6/14)+ 8/14 * log2(8/14) ) = 0.985

 

信息增益率

信息增益对属性值种类较多的属性比较偏好，为了解决这一问题，提出了信息增益率。但信息增益率对可取值数目较少的属性有所偏好，因此C4.5算法采用先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的方法来选择最优划分属性。

GainRation( S, “天气”) = 0.246/ 1.577 = 0.155

GainRation( S, “温度”) = 0.029/ 1.556 = 0.019

GainRation( S, “湿度”) = 0.151/ 1.0 = 0.151

GainRation( S, “风速”) = 0.048/ 0.985 = 0.048

可以发现，这里采用C4.5算法，仍是选取“天气”作为第一个分裂属性，最终得到一个由信息增益率选择特征得到的决策树。

 

基尼系数

假设有数据集S，且S有K个分类，那么可定义基尼指数为：

，  

从公式可以看到，基尼指数的意义是：从数据集S中随机抽取两个样本，其类别不同的概率。直觉地，基尼指数越小，则数据集S的纯度越高。和信息增益不一样，选择特征时信息增益值越大特征越佳，而选择Gini系数时，值越小的特征越佳

相对于用信息增益/信息增益率来作为决策指标，基尼指数的运算量比较小，也很易于理解，这是CART算法使用基尼指数的主要目的。

Gini( S, “天气”) =  5/14 * [1 -  (3/5)^2 - (2/5)^2 ] + 4/14 * [1 - (4/4)^2 ] + 5/14 * [1 -  (3/5)^2 - (2/5)^2 ] = 0.343

Gini( S, “温度”) =  4/14 * [1 -  (3/4)^2 - (1/4)^2 ] + 6/14 * [1 -  (4/6)^2 - (2/6)^2 ] + 4/14 * [1 -  (2/4)^2 - (2/4)^2 ] = 0.440

Gini( S, “湿度”) =  7/14 * [1- (3/7)^2 - (4/7)^2 ] + 7/14 * [1 - (6/7)^2 - (1/7)^2 ]  = 0.367

Gini( S, “风速”) =  6/14 * [1- (3/6)^2 - (3/6)^2 ] + 8/14 * [1- (6/8)^2 - (2/8)^2 ] = 0.455

这里采用CART算法，仍然选取“天气”作为第一个分裂属性，最终也能得到一个由Gini系数选择特征得到的决策树。

---

小结

决策树的优点是易于理解，对中间值的缺失不敏感，可以处理不相关特征数据。缺点是可能会产生过度匹配（overfitting）问题。决策树的过程包括生成和剪枝，剪枝和代码部分，后面再继续更新。