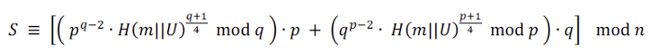预言机与 Rabin 签名在比特币智能合约中的应用原理
预言机(Oracle)1
比特币或其他区块链上的智能合约通常需要访问区块链外部的数据使之更加实用,例如:现实中保险合约中的天气变化或博彩合约中的体育比赛结果等。出于安全性考虑,在一个独立的沙箱内运行智能合约时,外部数据检索是禁止的。他们依赖第三方预言机(Oracle)来提供这些数据。这样就产生了一个“完整性”的问题,又称预言机问题(the Oracle problem)。需要使用数字签名来验证由已知的预言机提供数据的真实性与完整性。
本文介绍了一种有效的方法,可以验证和访问任意链上或链下由预言机在比特币智能合约内签署的任意数据。
Rabin 签名算法2
Rabin 签名算法是可用于替代比特币中使用的椭圆曲线数字签名算法(ECDSA)的另一种数字签名算法(DSA)。Rabin 数字签名的安全性由计算模合数平方根的计算复杂度保证,其难度近似于大整数质因数分解问题。
密钥生成
与 RSA 类似,密钥是通过确定两个大素数 p 和 q 来生成的。私钥是 (p, q) 的组合,其对应公钥 n = p * q 。
签名
将填充值 U 附加到要签名的消息 m 中,使得哈希值 h(m||U)3 于 S 的二次方模 n 同余。签名就是 (S, U) 的组合。
验证
可以通过使用签名 (S, U) , 消息 m 和公钥 n 检查上述等式是否成立来验证签名。
算法优势
由此可见,Rabin 签名具有非常好的非对称性,即签名生成需要大量的计算,而签名验证所需的计算量低。这个属性使得它非常适合链上实现,在链上实现中只需要签名验证。原则上,我们可以使用 ECDSA 来验证签名,但它的成本与 Rabin 相比要高出许多数量级。
实现
这里是一个 Rabin 算法的 Javascript 实现,包括密钥生成、签名生成和签名验证。
同时,我们也有一个 sCrypt 语言实现。注意,核心部分只有大约10行代码,只涉及基本的代数和哈希运算。我们只需要实现签名验证,因为这是链上唯一要完成的部分。
此外,我们还演示了一种生成较长哈希值(示例中为512位)的通用技术。方法是将原信息的 SHA256 哈希值结果分段后再次计算 SHA256 哈希值,并将其结果连接起来。完整代码如下所示。
import "util.scrypt";
contract RabinSignature {
public function verifySig(int sig, bytes msg, bytes padding, int n) {
int h = Util.fromLEUnsigned(this.hash(msg + padding));
require((sig * sig) % n == h % n);
}
function hash(bytes x) returns (bytes) {
// expand into 512 bit hash
bytes hx = sha256(x);
int idx = length(hx) / 2;
return sha256(hx[:idx]) + sha256(hx[idx:]);
}
}
结论
由于有了 Rabin 签名,我们可以将任意的数据签名后嵌入到比特币交易中,并使用现有的比特币脚本在链上有效地验证它。此外,还可以根据应用程序的安全需求自定义复杂性与成本,这比在共识层对特定的 DSA 进行硬编码更加灵活。如果需要更强的安全性,则可以简单地使用更长的密钥和哈希值。
通过允许智能合约安全可信的访问外部预言机数据,它们将变得异常强大。
致谢
感谢 nChain 的 Owen Vaughan 和 Craig Wright 博士对于在比特币中使用 Rabin 签名的探索与发现。
附录
预言机(Oracle):区块链外信息写入区块链内的机制,一般被称为预言机 (oracle mechanism),wiki 解释; ↩︎
Rabin 签名算法:一种非对称加密算法,wiki 解释 ↩︎
h(m||U):表示连接 m 和 U 后再整体计算哈希值; ↩︎