运筹系列18:routing模型之VRPTW问题
1. 问题模型
当VRP问题有到达时间的约束条件时,问题变为VRPTW(VRP with Time Windows)。
2. 例子
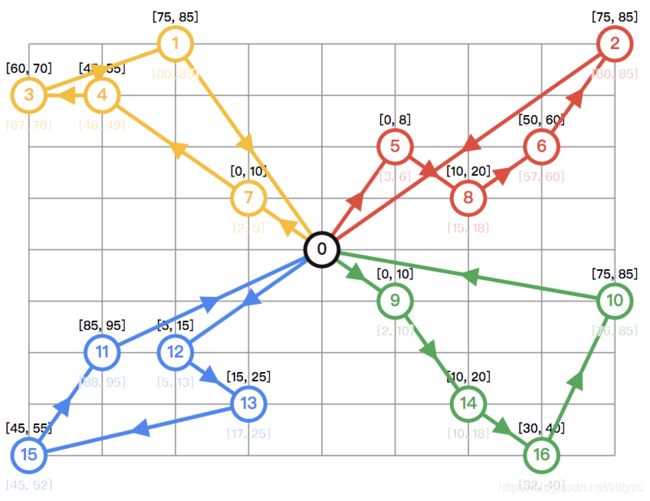
每个点右下角的数字表示需求,上方的两个数字表示开始服务的时间窗,车辆最大允许服务时间为120。单位服务时间=5*需求量,网格长度114,高度80,车辆速度83.33,使用曼哈顿距离。
使用如下代码添加时间窗约束:
index = routing.NodeToIndex(location_node)
time_dimension.CumulVar(index).SetRange(location_time_window[0], location_time_window[1])
使用如下代码获取货物和时间变量的数据:
load_var = capacity_dimension.CumulVar(index)
time_var = time_dimension.CumulVar(index)
"""Capacitated Vehicle Routing Problem with Time Windows (CVRPTW).
"""
from __future__ import print_function
from ortools.constraint_solver import pywrapcp
from ortools.constraint_solver import routing_enums_pb2
###########################
# Problem Data Definition #
###########################
def create_data_model():
"""Stores the data for the problem"""
data = {}
# Locations in block units
_locations = \
[(4, 4), # depot
(2, 0), (8, 0), # locations to visit
(0, 1), (1, 1),
(5, 2), (7, 2),
(3, 3), (6, 3),
(5, 5), (8, 5),
(1, 6), (2, 6),
(3, 7), (6, 7),
(0, 8), (7, 8)]
demands = [0, # depot
1, 1, # row 0
2, 4,
2, 4,
8, 8,
1, 2,
1, 2,
4, 4,
8, 8]
capacities = [15, 15, 15, 15]
time_windows = \
[(0, 0),
(75, 85), (75, 85), # 1, 2
(60, 70), (45, 55), # 3, 4
(0, 8), (50, 60), # 5, 6
(0, 10), (10, 20), # 7, 8
(0, 10), (75, 85), # 9, 10
(85, 95), (5, 15), # 11, 12
(15, 25), (10, 20), # 13, 14
(45, 55), (30, 40)] # 15, 16
# Multiply coordinates in block units by the dimensions of an average city block, 114m x 80m,
# to get location coordinates.
data["locations"] = [(l[0] * 114, l[1] * 80) for l in _locations]
data["num_locations"] = len(data["locations"])
data["num_vehicles"] = 4
data["depot"] = 0
data["demands"] = demands
data["vehicle_capacities"] = capacities
data["time_windows"] = time_windows
data["time_per_demand_unit"] = 5
data["vehicle_speed"] = 83.33
return data
#######################
# Problem Constraints #
#######################
def manhattan_distance(position_1, position_2):
"""Computes the Manhattan distance between two points"""
return (
abs(position_1[0] - position_2[0]) + abs(position_1[1] - position_2[1]))
def create_distance_callback(data):
"""Creates callback to return distance between points."""
_distances = {}
for from_node in range(data["num_locations"]):
_distances[from_node] = {}
for to_node in range(data["num_locations"]):
if from_node == to_node:
_distances[from_node][to_node] = 0
else:
_distances[from_node][to_node] = (
manhattan_distance(data["locations"][from_node],
data["locations"][to_node]))
def distance_callback(from_node, to_node):
"""Returns the manhattan distance between the two nodes"""
return _distances[from_node][to_node]
return distance_callback
def create_demand_callback(data):
"""Creates callback to get demands at each location."""
def demand_callback(from_node, to_node):
return data["demands"][from_node]
return demand_callback
def add_capacity_constraints(routing, data, demand_evaluator):
"""Adds capacity constraint"""
capacity = "Capacity"
routing.AddDimensionWithVehicleCapacity(
demand_evaluator,
0, # null capacity slack
data["vehicle_capacities"], # vehicle maximum capacities
True, # start cumul to zero
capacity)
def create_time_callback(data):
"""Creates callback to get total times between locations."""
def service_time(node):
"""Gets the service time for the specified location."""
return data["demands"][node] * data["time_per_demand_unit"]
def travel_time(from_node, to_node):
"""Gets the travel times between two locations."""
if from_node == to_node:
travel_time = 0
else:
travel_time = manhattan_distance(
data["locations"][from_node],
data["locations"][to_node]) / data["vehicle_speed"]
return travel_time
def time_callback(from_node, to_node):
"""Returns the total time between the two nodes"""
serv_time = service_time(from_node)
trav_time = travel_time(from_node, to_node)
return serv_time + trav_time
return time_callback
def add_time_window_constraints(routing, data, time_callback):
"""Add Global Span constraint"""
time = "Time"
horizon = 120
routing.AddDimension(
time_callback,
horizon, # allow waiting time
horizon, # maximum time per vehicle
False, # Don't force start cumul to zero. This doesn't have any effect in this example,
# since the depot has a start window of (0, 0).
time)
time_dimension = routing.GetDimensionOrDie(time)
for location_node, location_time_window in enumerate(data["time_windows"]):
index = routing.NodeToIndex(location_node)
time_dimension.CumulVar(index).SetRange(location_time_window[0], location_time_window[1])
###########
# Printer #
###########
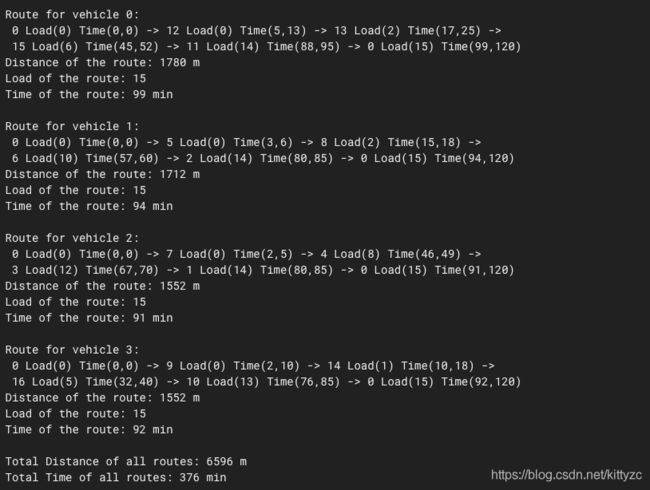
def print_solution(data, routing, assignment):
"""Prints assignment on console"""
# Inspect solution.
capacity_dimension = routing.GetDimensionOrDie('Capacity')
time_dimension = routing.GetDimensionOrDie('Time')
total_dist = 0
time_matrix = 0
for vehicle_id in range(data["num_vehicles"]):
index = routing.Start(vehicle_id)
plan_output = 'Route for vehicle {0}:\n'.format(vehicle_id)
route_dist = 0
while not routing.IsEnd(index):
node_index = routing.IndexToNode(index)
next_node_index = routing.IndexToNode(
assignment.Value(routing.NextVar(index)))
route_dist += manhattan_distance(
data["locations"][node_index],
data["locations"][next_node_index])
load_var = capacity_dimension.CumulVar(index)
route_load = assignment.Value(load_var)
time_var = time_dimension.CumulVar(index)
time_min = assignment.Min(time_var)
time_max = assignment.Max(time_var)
plan_output += ' {0} Load({1}) Time({2},{3}) ->'.format(
node_index,
route_load,
time_min, time_max)
index = assignment.Value(routing.NextVar(index))
node_index = routing.IndexToNode(index)
load_var = capacity_dimension.CumulVar(index)
route_load = assignment.Value(load_var)
time_var = time_dimension.CumulVar(index)
route_time = assignment.Value(time_var)
time_min = assignment.Min(time_var)
time_max = assignment.Max(time_var)
total_dist += route_dist
time_matrix += route_time
plan_output += ' {0} Load({1}) Time({2},{3})\n'.format(node_index, route_load,
time_min, time_max)
plan_output += 'Distance of the route: {0} m\n'.format(route_dist)
plan_output += 'Load of the route: {0}\n'.format(route_load)
plan_output += 'Time of the route: {0} min\n'.format(route_time)
print(plan_output)
print('Total Distance of all routes: {0} m'.format(total_dist))
print('Total Time of all routes: {0} min'.format(time_matrix))
########
# Main #
########
def main():
"""Entry point of the program"""
# Instantiate the data problem.
data = create_data_model()
# Create Routing Model
routing = pywrapcp.RoutingModel(data["num_locations"], data["num_vehicles"], data["depot"])
# Define weight of each edge
distance_callback = create_distance_callback(data)
routing.SetArcCostEvaluatorOfAllVehicles(distance_callback)
# Add Capacity constraint
demand_callback = create_demand_callback(data)
add_capacity_constraints(routing, data, demand_callback)
# Add Time Window constraint
time_callback = create_time_callback(data)
add_time_window_constraints(routing, data, time_callback)
# Setting first solution heuristic (cheapest addition).
search_parameters = pywrapcp.RoutingModel.DefaultSearchParameters()
search_parameters.first_solution_strategy = (
routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC)
# Solve the problem.
assignment = routing.SolveWithParameters(search_parameters)
if assignment:
printer = print_solution(data, routing, assignment)
if __name__ == '__main__':
main()