解最优化问题

解最优化问题

本文版权属于重庆大学计算机学院刘骥，禁止转载

最优化问题的分类

按照目标函数的可导性，可以将最优化问题分为两类：
1. 目标函数可导，例如目标函数为 f(x)=x2+x+1
2. 目标函数不可导，例如目标函数为 f(X)=∑p∈Xep

对于不可导的目标函数，其解法比较特殊。采用模拟退火算法、粒子群算法、遗传算法、蚁群算法、图割（Graph Cut）算法等方法，可以求解这类问题，但通常无法得到精确的解（或者说全局最优解）。并且有些问题，仅能用特定的解法，求出特定的解。由于该类问题的复杂性，本文对不可导目标函数问题不进行讨论。如果你在实际中遇到了这类问题，可以采用如下方法解决：
查学术论文，github上找代码；如果找不到解决方案，恭喜你，这是一个获得数学大奖的机会

本文余下部分，针对可导的目标函数进行讨论，这类问题存在大量通用的算法。人类历史发展到2017年，你甚至不需要了解具体算法的原理，也能够很happy的解决这类问题。

直接开始求解

下面我们用一个简单的最优化问题为例：

argminx,yf(x,y)=x2+y2+1

显然 x=0，y=0 时， f(x,y) 有最小值1。问题在于，计算机如何求解这个问题呢？

downhill simplex

Python语言的scipy.optimize包的fmin函数实现了downhill simplex方法，也称为Nelder–Mead方法（downhill、simplex和downhill simplex是不同的概念，有兴趣可以参考维基百科）。这里不去讲解downhill simplex的原理，有需要原理的读者，请移步到https://en.wikipedia.org/wiki/Nelder–Mead_method。
fmin函数的说明如下：

我估计你看不懂，所以我不准备解释。我们直接看代码吧。

# encoding=utf-8
import scipy.optimize as opt
#定义目标函数f
def f(X):
    x=X[0]
    y=X[1]
    return x**2+y**2+1;
x=10
y=10
X=[x,y]
X=opt.fmin(f,X) #f是目标函数，X是初始猜测的解
x=X[0]
y=X[1]
print x,y 

程序执行结果如下：

最终 x 和 y 的值不是0，而是一个接近0的值。这是由于数值计算毕竟是缺乏精度的。fmin函数是一个迭代算法。在执行过程中，它还同时输出了结束迭代时的最小值，迭代的次数，以及函数计算的次数。

Conjugate Gradient

downhill simplex比较简单，实现没有难度。但它的问题在于比较慢，下面我们试试 Conjugate Gradient法。使用scipy.optimize包的fmin_cg方法。这个方法需要求出目标函数的偏导数（梯度）：

∂f∂x=2x∂f∂y=2y

# encoding=utf-8
import scipy.optimize as opt
import numpy as np
#定义目标函数f
def f(X):
    x=X[0]
    y=X[1]
    return x**2+y**2+1;
#定义目标函数f对应的梯度函数
def gradf(X):
    x=X[0]
    y=X[1]
    gx=2*x
    gy=2*y
    return np.asarray((gx,gy)) #梯度以向量形式返回
x=10
y=10
X=[x,y]
X=opt.fmin_cg(f,X,fprime=gradf) #f是目标函数，X是初始猜测的解，增加梯度
x=X[0]
y=X[1]
print x,y 

运行结果如下：

可以看出该方法比downhill simplex运行得更快。当然这是显然的，因为有了梯度信息。

你居然不会求偏导数！

OK！OK！有办法可以解决！今年是2017年，如果你还不会求偏导数，那么交给计算机吧！

X=opt.fmin_cg(f,X)

OK！计算结果如下：

慢了一些，函数的演化次数增加了15次，why？因为算法用数值法来计算梯度！具体来说（你可以忽略下面的内容，把问题交给人工智能）：

def gradf(X):
    x=X[0]
    y=X[1]
    gx=(f([x+0.0000001,y])-f([x,y]))/0.0000001
    gy=(f([x,y+0.0000001])-f([x,y]))/0.0000001
    return np.asarray((gx,gy))

也就是：

f′(x)=f(x+Δx)−f(x)Δx

Newton-CG

试试Newton-CG，也就是fmin_ncg函数，该函数需要2阶偏导数构成的Hessian矩阵：

⎡⎣⎢⎢⎢⎢∂f2∂x2∂f2∂y∂x∂f2∂x∂y∂f2∂y2⎤⎦⎥⎥⎥⎥=[2002]

代码如下：

# encoding=utf-8
import scipy.optimize as opt
import numpy as np
#定义目标函数f
def f(X):
    x=X[0]
    y=X[1]
    return x**2+y**2+1;
#定义目标函数f对应的梯度函数
def gradf(X):
    x=X[0]
    y=X[1]
    gx=2*x
    gy=2*y
    return np.asarray((gx,gy)) #梯度以向量形式返回
def hess(X):
    return np.array([[2,0],[0,2]]) #hessian矩阵
x=10
y=10
X=[x,y]
X=opt.fmin_ncg(f,X,fprime=gradf,fhess=hess) #f是目标函数，X是初始猜测的解，增加梯度
x=X[0]
y=X[1]
print x,y 

运行结果如下：

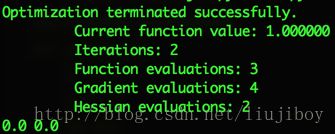
非常精确！当然如果不会计算hessian，如下操作：

X=opt.fmin_ncg(f,X,fprime=gradf) #注意梯度是必须的

结果如下：

总结

现在是2017年，基本的最优化问题已经经过了几百年的发展（不是几十年），因此有大量现成的函数库可以使用。直接调用这些库函数，你甚至不需要知道如何求导数、如何求Hessian矩阵，也可以很好的解决最优化问题（可导的）。如果不追求效率，如果精度可以接受，那么最最原始的downhill simplex方法已经能够适用于大多数场景（你需要小数点后几位的精度？）。

数学原理

大多数最优化的书籍，在讲解数学原理时，都抱着一定要让人看不懂，才能显得高深莫测的心态。其实求解可导目标函数的数学原理是极其简单的，那就是：穷举，更高效的穷举。

假设目标函数为 f(X) ，其中 X∈Rn （注意这意味着 X 是一个向量， f 是多元函数）。例如 X=(x,y,z)T ，则 f(X) 表示的函数就是 f(x,y,z) 。我如此定义不是为了把你搞晕，而是为了环保！试想如果我想定义函数 f(x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19,x20,x21,x22) ，难道不是写成 f(X) ， X∈R22 更环保吗？Yes，Yes，你从来没有见过3元以上的函数，那不是因为你一直都是在做考题吗？一道考试题，要是有22个变量，你要用多大的草稿纸？现实问题则不然，考虑女性择偶问题，男方必须有钱、长得帅、有安全感、父母双亡、有车、有房、有股票、有存款、初恋、非凤凰男等等。表示为函数就是：

f(钱,颜值,安全感,父母,车,房,股票,存款,情史,是否凤凰男)

学过代数吧？于是这个函数就变成了:

f(x1,x2,x3,x4,x5,x6,x7,x8,x9,x10)=f(X)

现在我们来讨论女性择偶函数f(X)的最优化！假定女性朋友给出的函数是这样的：

f(X)=XTC10×10X

这是一个二次函数（请自行展开），C是系数矩阵（我们只是假设女性朋友给出了这样的二次函数，真实情况未必）。OK，其实这个函数长什么样子，不影响后面的讨论。我们所要讨论的是 f(X) 可导的情况。如何确定 f(X) 的极值呢？

最笨的方法就是穷举！！换言之，先试试 f(X1) ，再看看 f(X2) ，不停的尝试 f(Xi) ，直到成为单身贵族……对，我告诉你的解法就是成为单身贵族的解法，因为解空间几乎是无限大的，穷举法太笨！

聪明一点的方式是穷举n次，找其中的最优。先试试 f(X1) ，再看看 f(X2) ，不停的尝试直到 f(Xn) ，找出 f(X1)到f(Xn) 中最优的 f(Xi) 。这个方法的缺陷在于，女性朋友不一定能够找到真正的灵魂伴侣。

再聪明一点的方法固定一些变量，搜索另外一些变量。必须长得帅，像鹿晗；必须有钱，和王思聪一样；必须是初恋。你看解空间一下就变小了。接下来的搜索就简单了很多。如果找不到解，那么就修改某些固定的变量。为什么长相必须像鹿晗？郭德纲也可以接受！这样我们就可以开始新的搜索啦！事实上，这就是绝大多数人，择偶的方式。

如果变量是连续的呢？数学家发现，在这种情况下，搜索策略其实是这样的：
1. 首先选择一个起始的解 X0 。
2. 比较 f(X0+Δ) ，如果 f(X0+Δ)<f(X0) 那么 X0+Δ 是更好的解
3. 另 X1=X0+Δ ，跳到第1步重新执行。

上述方法的核心在于存在一个 X 的更新公式：

Xn+1=Xn+Δn

上述算法有三个终止条件：
1. 迭代次数达到限额（都已经120岁的单身贵族啦！）
2. Δn 趋近于0
3. f(Xn)−f(Xn+1) 趋近于0

下面举个例子，目标函数如下：

f(x,y)=x2+y2+1

假设初始值为 X0=(1,1)T ，令 Δn=(−0.1,−0.1)T ，于是：

X0=(1,1)TX1=(0.9,0.9)T......X10=(0,0)TX11=(−0.1,−0.1)T

Stop！不是 X10 已经达到最优了吗？为什么程序还在跑？问题在于那个 Δn ，如果它能够越接近最小值越小，程序不就可以停下来了吗？越接近你的灵魂伴侣，越需要放慢搜索的速度不是吗？
怎么解决这个问题呢？数学家出场了。我们知道 f(Xn+1)=f(Xn+Δn) ，根据泰勒公式展开就是：

f(Xn+1)=f(Xn+Δn)=f(Xn)+∂f(Xn)∂XΔn+ΔTn∂f2(Xn)∂X2Δn/2+......

针对该公式求 Δn 的导数，并令结果等于0，则：

∂f(Xn)∂X+∂f2(Xn)∂X2Δn=0∂f2(Xn)∂X2Δn=−∂f(Xn)∂X

现在我们可以解出 Δn ！如果你对上述推导的原理感到好奇，不奇怪啊，你不是数学家对吧？总之，我们会算就可以啦。现在用新的公式来求解老问题。

f(x,y)=x2+y2+1∂f(x,y)∂x=2x∂f(x,y)∂y=2y∂f2(x,y)∂x2=2∂f2(x,y)∂x∂y=0∂f2(x,y)∂y2=2∂f(x,y)∂y∂x=0[2002]Δn=−[2xn2yn]Δn=−[xnyn]

计算过程如下：

X0=(1,1)TΔ0=(−1,−1)TX1=X0+Δ0=(0,0)TΔ1=(0,0)T∵Δ1=(0,0)T∴X=X1就是最优解

数学白痴表示求偏导数矩阵太难理解！！如何破！！数学家马上送上福利：

λΔn=−∂f(Xn)∂X

假设 λ=2 ，我们看看目标函数 f(x,y)=x2+y2+1 的计算过程：

Δn=−[xnyn]X0=(1,1)TΔ0=(−1,−1)TX1=X0+Δ0=(0,0)TΔ1=(0,0)T∵Δ1=(0,0)T∴X=X1就是最优解

运气不错！如果 λ=4 呢？推导如下：

Δn=−[0.5xn0.5yn]X0=(1,1)TΔ0=(−0.5,−0.5)TX1=X0+Δ0=(0.5,0.5)TΔ1=(−0.25,−0.25)TX2=X1+Δ1=(0.25,0.25)TΔ2=(−0.0625,−0.0625)T......若干步后收敛

如果 λ=1 ，推导如下：

Δn=−[2xn2yn]X0=(1,1)TΔ0=(−2,−2)TX1=X0+Δ0=(−1,−1)TΔ1=(2,2)TX2=X1+Δ1=(1,1)TΔ2=(−2,−2)T......无法收敛

可见如果采用新的计算公式， λ 的取值会影响算法的收敛速度，甚至无法收敛。但的确这种算法避免了计算Hessian，数学白痴非常高兴！那么它存在的问题可以解决吗？当然可以，方法就是 动态调整 λ 的取值，从而加快收敛，避免震荡。
最后，再来考虑一下，如果数学白痴连梯度都不会算怎么办？Nelder–Mead Method！对有高等数学背景的人而言，理解Nelder–Mead Method反而很困难！这里就不再详谈了。

数学白痴的福利

我们都不喜欢数学，还好现在是2017年，大量的工作已经由擅长数学的科学家做完了。你所需要的就是找一个算法丰富的库！比如Python的scipy或者matlab。为了写作本文，我对最优化问题进行了很多简化，首先只考虑可导的目标函数，其次也没有考虑函数变量的条件约束（比如 X 必须是整数、 X 必须大于0）。但无论问题多么复杂，这些问题已经被充分研究，充分解决。99%的情况，你只需要scipy或者matlab，剩下0.9999%的情况需要github。最后，还剩下一丢丢的未知领域，等待着学者去研究。别抢他们的饭碗，茶叶蛋已经够贵的啦！