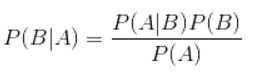朴素贝叶斯(Naive Bayesian)_社区不良用语识别

贝叶斯定理:

首先介绍下贝叶斯定理：

这个在250多年前发明的算法，在信息领域内有着无与伦比的地位。贝叶斯分类是一系列分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。朴素贝叶斯算法（Naive Bayesian) 是其中应用最为广泛的分类算法之一。

朴素贝叶斯分类器基于一个简单的假定：给定目标值时属性之间相互条件独立。

通过以上定理和“朴素”的假定，我们知道：

P( Category | Document) = P ( Document | Category ) * P( Category) / P(Document)

其实就是

朴素贝叶斯分类:

机器学习中使用的朴素贝叶斯分类就是基于贝叶斯定理,通过对P(B|A)的计算测试数据所属各分类(视为相互独立)的可能性,并选取其中概率最高的那一类作为答案.

 

例:社区不良用语识别

这里用的是 机器学习实战 的例子.

1.  收集数据.
2. 准备,分析数据:语句分类标记,分词.
3. 训练算法:计算不同独立特征条件的概率.
4. 测试算法:使用测试数据集测试计算错误率.
5. 使用算法.

1.收集数据

def loadDataSet():
#词条切分后的语句集合，列表每一行代表一个文档
    postingList=[['my','dog','dog','flea',\
                  'problems','help','please'],
                 ['maybe','not','take','him',\
                  'to','dog','park','stupid'],
                 ['my','dalmation','is','so','cute',
                  'I','love','him'],
                 ['stop','posting','stupid','worthless','garbage'],
                 ['my','licks','ate','my','steak','how',\
                  'to','stop','him'],
                 ['quit','buying','worthless','dog','food','stupid']]
    #标注的每段语句的分类标签
    classVec=[0,1,0,1,0,1]
    return postingList,classVec

2.准备分析数据

首先我们要记录所有的语句中出现过的单词:

def createVocabList(dataSet):
    vocabSet=set([])
    for document in dataSet:
        vocabSet=vocabSet|set(document)
    return list(vocabSet)

这里我们先用集合存储各语句中出现过得单词并保证了其的唯一性,然后转换成列表返回一遍后面操作

然后根据得到的列表获得各语句中的各单词是否出现并以0(无),1(有)记录

#vocaSet:所有语句中出现的单词,inputSet:输入的测试语句
def setOfWords2Vec(vocabSet,inputSet):
    returnVec=[0]*len(vocabSet)       #使用vocaSet的长度以便之后统计用
    for word in inputSet:
        if word in vocabSet:
            returnVec[vocabSet.index(word)]=1
        else: print('the word: %s is not in my vocabulary! '%'word')
    return returnVec

3.训练算法

接下来通过对 各分类中语句的各个单词统计 除以 分类中的单词个数 计算得到各单词属于各分类的概率.

#trainMatrix:前一步获得的各语句向量,classLabel:标记的各语句分类
def trainb(trainMatrix, classLabel):
    numTrainDocs = len(trainMatrix)
    numWords = len(trainMatrix[0])
    pBase = sum(classLabel) / float(numTrainDocs)
    p0Num = zeros(numWords)
    p1Num = zeros(numWords)
    p0Denom = 0.0
    p1Denom = 0.0
    for i in range(numTrainDocs):
        if classLabel[i] == 1:
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])          
        else:
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i]) 
    p0 = p0Num / p0Denom
    p1 = p1Num / p1Denom
    return p0, p1, pBase

返回的p0,p1分别是每个单词在各分类下的概率,pBase是各分类的概率.

这各还是有些问题的,

• 在计算像p(w0|ci)p(w1|ci)p(w2|ci)这样的式子如果有一个概率是0最后乘机也就为0了,所以应把6-9行改为

p0Num = ones(numWords)
p1Num = ones(numWords)
p0Denom = 2.0
p1Denom = 2.0

• 当太多过小的数相成会造成下溢(Python四舍五入后为0),所以把倒数3-2行改为

p0 = log(p0Num / p0Denom)
p1 = log(p1Num / p1Denom)

当改为log()后其图像虽有所改变,但它俩的递增区间和递减区间以及在相同点上取得机制极值.

4.测试算法

def classifyNB(vec2Classify,p0Vec,p1Vec,pClass1):
    #计算测试数据属于各分类的概率
    p1=sum(vec2Classify*p1Vec)+log(pClass1)
    p0=sum(vec2Classify*p0Vec)+log(1.0-pClass1)
    if p1>p0:
        return 1
    else:
        return 0

5.使用

def testingNB():
    listOPosts,listClasses=loadDataSet()
    myVocabList=createVocabList(listOPosts)
    trainMat=[]
    for postinDoc in listOPosts:
        trainMat.append(setOfWords2Vec(myVocabList,postinDoc))\
    p0V,p1V,pAb=trainb(array(trainMat),array(listClasses))
    

#测试
    testEntry=['love','my','dalmation']
    thisDoc=array(setOfWords2Vec(myVocabList,testEntry))
    print(testEntry,'classified as:',classifyNB(thisDoc,p0V,p1V,pAb))

    testEntry1=['stupid','garbage']
    thisDoc1=array(setOfWords2Vec(myVocabList,testEntry1))
    print(testEntry,'classified as:',classifyNB(thisDoc1,p0V,p1V,pAb))

运行结果

(['love', 'my', 'dalmation'], 'classified as:', 0)
(['love', 'my', 'dalmation'], 'classified as:', 1)