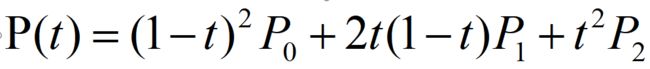OpenGL——使用几何着色器绘制平滑（bezier）曲线

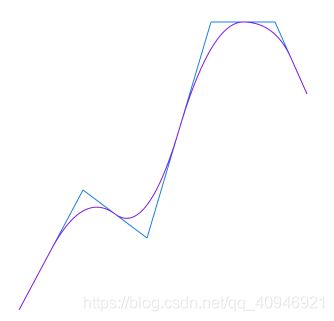
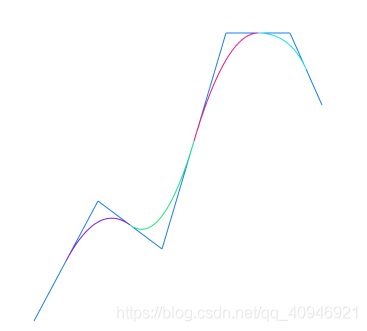
效果图：

顶点数据

    float vertices[]={
        -0.6f, -0.8f,  0.0f,        //首尾填充
        -0.6f, -0.8f,  0.0f,
        -0.4f, -0.3f,  0.0f,
        -0.2f, -0.5f,  0.0f,
         0.0f,  0.4f,  0.0f,
         0.2f,  0.4f,  0.0f,
         0.3f,  0.1f,  0.0f,
         0.3f,  0.1f,  0.0f
    };

关于几何着色器：

其作用大致是：根据已有顶点数据，构建出新的顶点数据，甚至修改图元。

关于Bezier曲线，可以看这篇文章：传送门

这里我们使用二阶Bezier方程

因此我们需要三个点（起点、一个控制点、终点）才能绘制一段Bezier曲线，我们需要考虑两个问题：

如何选取控制点？

这里我的策略是，每三个连续点（p0，p1，p2），取两条线（p0p1，p1p2）的中点作为起点和终点，中间点（p1）作为控制点，也就是下图的效果：

这三个点从哪来？

由于我们的顶点数据本意是用来构建GL_LINE_STRIP的，但GL_LINE_STRIP图元只会传递两个顶点数据给几何着色器，而我们绘制bezier曲线需要三个顶点。很显然GL_LINE_STRIP已经无法满足我们了，因此我们需要使用GL_TRIANGLE_STRIP。真奇怪，我们现在正使用三角形图元来画线。

还没完，使用GL_TRIANGLE_STRIP有一个细节，假设有一系列顶点分别为（0，1，2，3，4，5）。使用GL_TRIANGLE_STRIP第一个绘制的三角形顶点是（0，1，2）, 重点来了，第二个三角形的顶点是（1，2，3）吗？

既然我这么问了，那肯定不是了，其实第二个三角形的顶点是（2，1，3），为什么会这样？

这个顺序是为了保证所有的三角形都是按照相同的方向绘制的，使这个三角形串能够正确形成表面的一部分。对于某些操作，维持方向是很重要的，比如剔除。

具体规律请看这篇文章：传送门

为了避免这一问题，我们需要让几何着色器能够识别出顶点的处理顺序。我们需要借助顶点着色器输出顶点的序号。

顶点着色器

#version 330 core

layout (location = 0) in vec3 pos;

out VS_OUT{
    int id;
} vs_out;

void main()
{
     gl_Position = vec4(pos,1.0f);
     vs_out.id = gl_VertexID;
}

几何着色器

#version 330 core

in VS_OUT {
    int id;
}gs_in[];
layout (triangles) in;                      //以三角形为单位进行扩张，每次从VertexShader往GeomShader传进三个点进行数据处理
layout (line_strip, max_vertices = 32) out; //将一个点变为最多32个可连成线条的点 交给FragShader

void creatBezier(){

    const int max_len=20;                   //使用20条线来绘制一段bezier曲线
    
    vec4 p0=mix(gl_in[0].gl_Position,gl_in[1].gl_Position,0.5);     //取前两个点的中点
    vec4 p1;
    vec4 p2;
    if(gs_in[2].id%2==0){
        p1=gl_in[1].gl_Position;                                    //调整点
        p2=mix(gl_in[1].gl_Position,gl_in[2].gl_Position,0.5);      //取后两个点的中点
    }
    else{
        p1=gl_in[0].gl_Position;                                    //同上
        p2=mix(gl_in[0].gl_Position,gl_in[2].gl_Position,0.5);
    }
    for(int i=0;i<=max_len;i++){                                    //根据公式生成顶点，并提交
        float t=i*0.05;
        gl_Position=p0*(1.0-t)*(1.0-t)+p1*2*t*(1.0-t)+p2*t*t;
        EmitVertex();
    }
    EndPrimitive();
}


void main(){
    creatBezier();
}

端点bug

使用上方的方式无法绘制两端的端点连线，比较好的解决方法是，把第一个点再添加到开始，末尾的点再添加到末尾

    float vertices[]={
        -0.6f, -0.8f,  0.0f,
        -0.4f, -0.3f,  0.0f,
        -0.2f, -0.5f,  0.0f,
         0.0f,  0.4f,  0.0f,
         0.2f,  0.4f,  0.0f,
         0.3f,  0.1f,  0.0f,
    };

    float vertices[]={
        -0.6f, -0.8f,  0.0f,        //首尾填充
        -0.6f, -0.8f,  0.0f,
        -0.4f, -0.3f,  0.0f,
        -0.2f, -0.5f,  0.0f,
         0.0f,  0.4f,  0.0f,
         0.2f,  0.4f,  0.0f,
         0.3f,  0.1f,  0.0f,
         0.3f,  0.1f,  0.0f
    };