机器学习：SVM支持向量机理解

SVM应该是机器学习过程中第一个特别复杂的算法了，其中大量的数学推导公式和优化算法，对小白真的太不友好了。这篇文章参考了许多优秀博文，主要是了解一下SVM，尽量少涉及复杂的公式推导，有些直接给出结论。如果对SVM的推导公式有兴趣，网上有大量的推导文章可以参考。

1 什么是SVM

SVM的英文全称是Support Vector Machines，中文叫支持向量机。它是一种有监督的机器学习算法，可用于分类或回归问题。SVM相对于其他分类算法，最大的好处就应该是他可以引入核函数，可以进行非线性分类。

2 一些基本概念

如下图，在二维空间上，两类点被一条直线完全分开叫做线性可分。

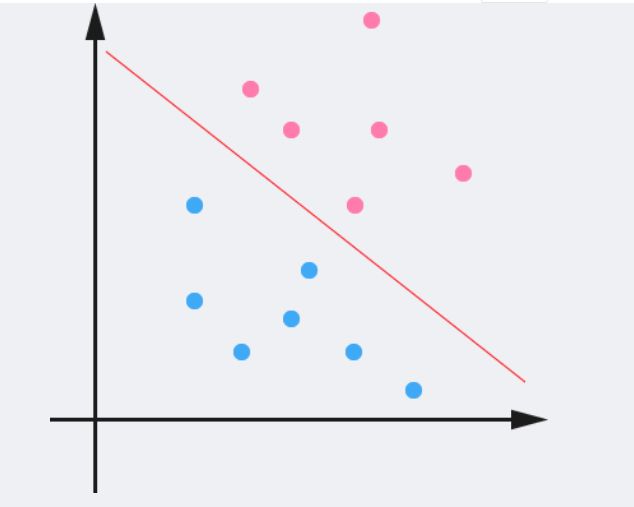
将数据集分隔开来的直线称为分隔超平面（separating hyperplane）。在上面给出的例子中，由于数据点都在二维平面上，所以此时分隔超平面就只是一条直线。但是，如果所给的数据集是三维的，那么此时用来分隔数据的就是一个平面。显而易见，更高维的情况可以依此类推。如果数据集是1024维的，那么就需要一个1023维的某对象来对数据进行分隔。这个1023维的某对象到底应该叫什么？N-1维呢？该对象被称为超平面（hyperplane），也就是分类的决策边界。分布在超平面一侧的所有数据都属于某个类别，而分布在另一侧的所有数据则属于另一个类别。
但是线性可分的数据集，可能有无数个分隔超平面。如下图，两种都可以把数据集分开，但是他们的分隔效果是一样的吗？显然第一个的分类效果是更好的，因为它具体更好的鲁棒性或者说健壮性。怎么理解鲁棒性，就是犯错误的几率小，也就是当新加进来一个点，能把新的点分类正确的可能性更大。

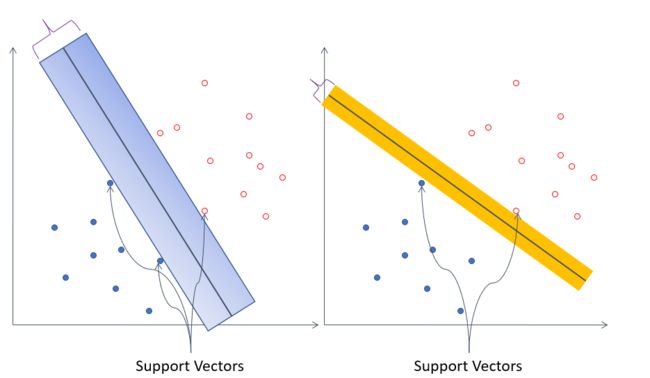
我们希望找到离分隔超平面近的点，确保它们离分隔面的距离尽可能远。这里点到分隔面的距离被称为间隔（margin）。我们希望间隔尽可能地大，这是因为如果我们犯错或者在有限数据上训练分类器的话，我们希望分类器尽可能健壮。支持向量（support vector）就是离分隔超平面近的那些点。由支持向量构成的平面为决策边界。SVM就是要找到支持向量并最大化间隔。

函数间隔和几何间隔：
一般来说，一个点距离分隔超平面的远近可以表示分类预测的确信程度。在超平面wx+b=0确定的情况下，|wx+b|能够相对地表示点x距离超平面的远近。而wx+b的符号和标记y的符号能否一致表示分类的正确性。所以可以用y(wx+b)来表示分类的正确性和确信度，这就是函数间隔的概念。
在逻辑回归中，y有0和1，而在这里，我们用1和-1来表示分类结果。为什么用1和-1呢。在二分类中，我们假定，当wx+b>0时，分类结果为1，wx+b<0时，分类结果为-1。这样的话，如果分类正确，y(wx+b)>0，且值越大确信度越高，如果分类错误，y(wx+b)<0，绝对值越大错的就越离谱。
函数间隔：对于给定的训练数据集T和超平面(w,b)，定义超平面(w,b)关于样本点(xi,yi)的函数间隔为

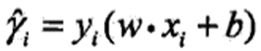
定义超平面(w,b)关于训练集T的函数间隔为超平面(w,b)关于T中所有样本点的(xi,yi)的函数间隔最小值，即

但是只有函数间隔是不够的，因为当成比例的改变w个b时，例如变成2w和2b，超平面没有改变，但是函数间隔变成原来的2倍了。因此，需要对分隔超平面的法向量加些约束，如规范化，|||w||=1，使得间隔是确定的。这时候函数间隔就成了几何间隔。其中||w||是w的范数，即为各个w的平方加起来开根号。
几何间隔：对于给定的训练数据集T和超平面(w,b)，定义超平面(w,b)关于样本点(xi,yi)的几何间隔为

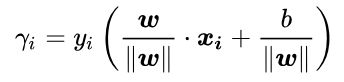
定义超平面(w,b)关于训练集T的函数间隔为超平面(w,b)关于T中所有样本点的(xi,yi)的函数间隔最小值，即

可以类比二维空间中点到直线距离公式理解：

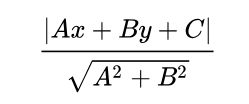
函数间隔和几何间隔的关系可以表示如下：

如果等比例改变w和b，超平面不变，函数间隔改变，几何间隔不变。

3 最大化间隔问题

根据支持向量的定义我们知道，支持向量到超平面的距离为 d，其他点到超平面的距离大于 d，于是有：

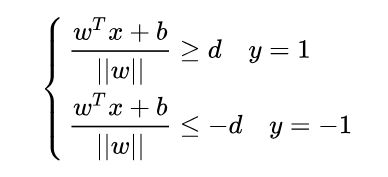
两边除以d，得到：

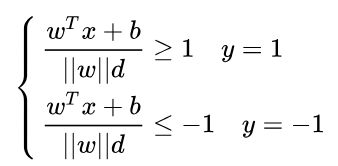
我们已经知道，改变w和b对我们的分隔超平面wx+b是没有影响的，所以这里令w^T=w^T/||w||d，b=b/||w||d，则化为：

合并两个方程则为：

在支持向量上，不等式即为等式，即y(W^Tx + b)=1，这就是决策边界。如下图：

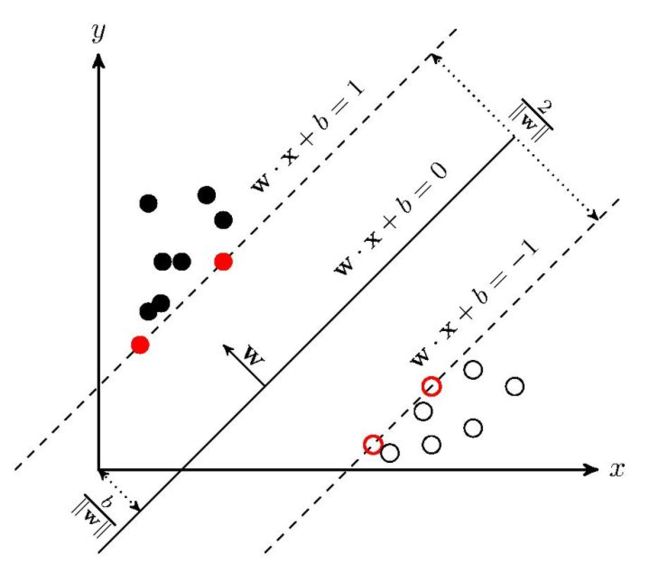
我们的几何间距也可以表示为：

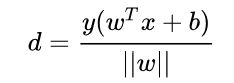
因为在支持向量上，分子为1，因此：

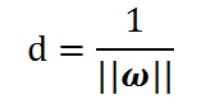
最大化d等价于最小化：

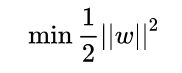
因此，求解最大间隔问题可以转化为下面的最优化问题：

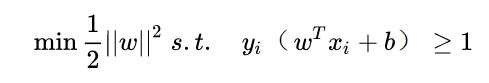
4 拉格朗日乘子法和KKT条件

上面我们已经得到了最大化间隔的优化问题，接下来如何求解呢？那就要用到拉格朗日乘子法了。由于涉及大量的数学优化知识，这里也可以省去，直接看结论，会用结论就可以满足我们求解SVM优化问题了。
拉格朗日函数主要用来求解带约束的优化问题，常见的优化问题有如下三种：
1.无约束优化问题

这类问题常常使用的方法就是Fermat定理，即使用求取f(x)的导数，然后令其为零，可以求得候选最优值，再在这些候选值中验证；如果是凸函数，可以保证是最优解。
2.有等式约束的优化问题

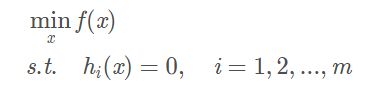
这类问题常用的方法为拉格朗日乘子法，构造拉格朗日函数：

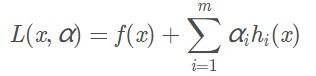
其中αi 为拉格朗日乘子。然后分别对x 和α=(α1,…,αm)^T求导并令导数为0：

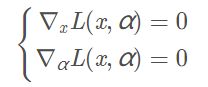
3.不等式约束的优化问题

构造拉格朗日函数：

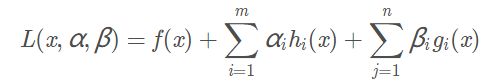
为了求出最优值，必须满足必要条件，就是KKT条件：

• 条件一：经过拉格朗日函数处理之后的新目标函数L(w,b,α)对x求导为零
• 条件二：h(x) = 0
• 条件三：α*g(x) = 0

对偶问题：
我们先定义对偶函数：

即对偶函数就是原问题对x最小化后关于α和β的函数。
则原问题的对偶问题为：

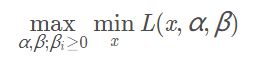
即原问题的对偶问题就是先求原问题关于x的最小值，再求关于α和β的的最大值。
对偶问题的解d与原问题的解p满足如下关系：

即对偶问题的解是原问题解的下确界。
这里有很重要一个结论：在KKT条件下，如果f(x)是凸函数，此时具有强对偶性，即等式成立，原问题的最优解等于对偶问题的最优解。因此我们可以通过求解对偶问题来求解原问题。
这里只给出结论，不做证明，只要会使用结论即可。那怎么使用呢？下面就针对SVM优化问题来使用这个结论。

5 求解SVM优化问题

在第三节，我们已经知道SVM优化问题如下：

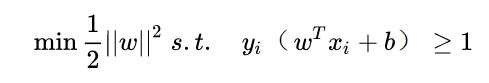
为了写出拉格朗日函数，把不等式条件转化为小于等于，我们把问题写为：

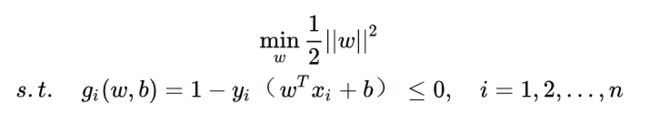
1.构造拉格朗日函数

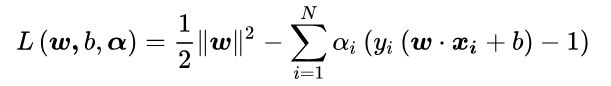
其中 αi 为拉格朗日乘子，且 αi>=0。
2.利用强对偶性转化

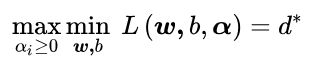
3.对参数w和b求偏导为0
求解凸函数的最小值，就是偏导为0的点。省去中间求解过程，得到最后结果为：

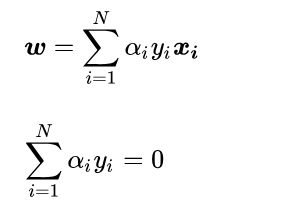
把上述结果带到原拉格朗日函数中，消去w和b：

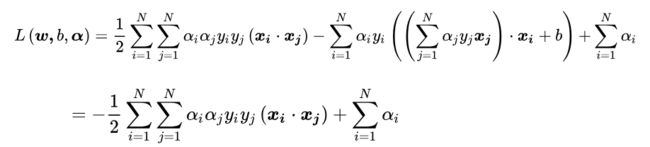
也就是说：

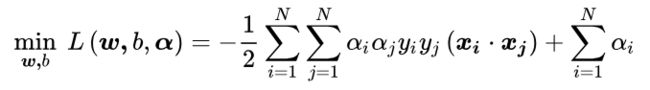
即拉格朗日函数对w和b求最小值后得到的结果。
则我们的对偶问题现在就是：

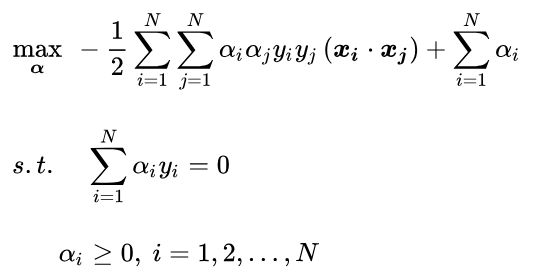
把目标式子加一个负号，将求解极大转换为求解极小：

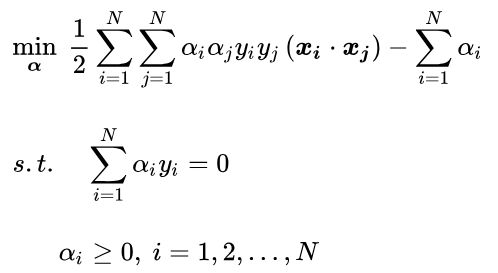
现在我们的优化问题变成了如上的形式。对于这个问题，一般使用序列最小优化（SMO）算法。下个章节我们再详细过一下SMO算法。我们通过这个优化算法能得到α*，是一个αi组成的n维向量。
4.求解w和b
根据α*，我们就可以求解出w和b。
根据前面偏导为0的推导，我们得到了：

因此可以求出w*。
注意KKT条件要满足：

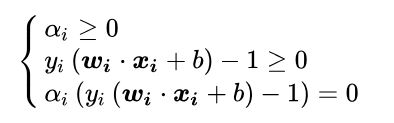
因此可以知道，在α*中至少存在一个αj>0（反证法可以证明，若全为0，则 w=0，这里w是指所有的参数wi组成的向量，矛盾）。对此 j有：

因此可以得到：

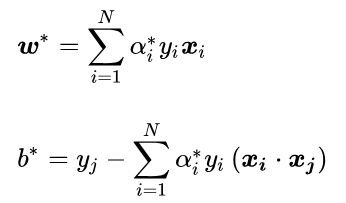
对于任意训练样本(xi,yi)，总有α_i=0或者y_j(wx_i+b)=1。若α_i=0 ，则该样本不会在最后求解模型参数的式子中出现。若α_i>0，则必有y_j(wx_i+b)=1，所对应的样本点位于最大间隔边界上，是一个支持向量。这显示出支持向量机的一个重要性质：训练完成后，大部分的训练样本都不需要保留，最终模型仅与支持向量有关。
5.求得分隔超平面和决策函数
所以最后得到分隔超平面：

分类决策函数：

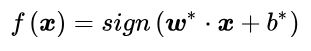
其中sign()为越阶函数：

6 软间隔

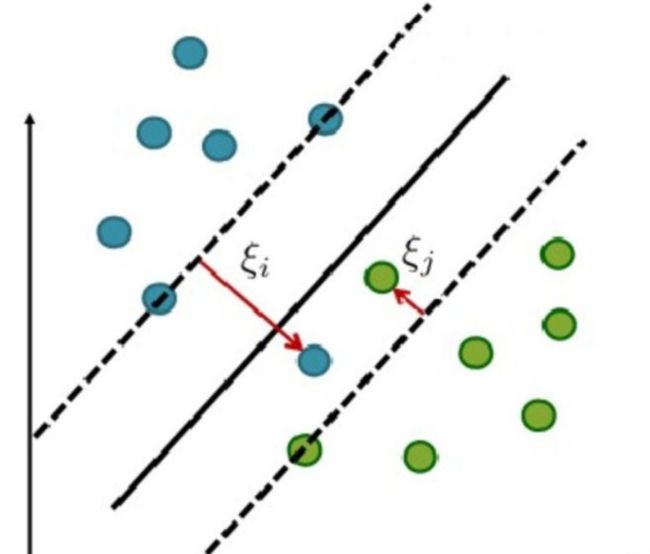
在实际应用中，完全线性可分的样本是很少的，如果遇到了不能够完全线性可分的样本，就要用到我们的软间隔了。相比于硬间隔的苛刻条件，我们允许个别样本点出现在间隔带里面，比如：

我们允许部分样本点不满足约束条件：

为了度量这个间隔软到何种程度，我们为每个样本引入一个松弛变量ξ_i，令ξ_i>=0，则有：

对应如下图所示：

增加软间隔后我们的优化目标变成了：

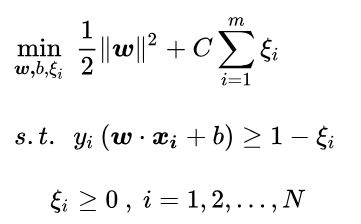
其中 C 是一个大于 0 的常数，可以理解为错误样本的惩罚程度，若 C 为无穷大，ξ_i 必然无穷小，如此一来线性 SVM 就又变成了线性可分 SVM；当 C 为有限值的时候，才会允许部分样本不遵循约束条件。
跟线性可分求解的思路一致，同样这里先用拉格朗日乘子法得到拉格朗日函数，再求其对偶问题。这里省去中间过程，得到最后的对偶问题为：

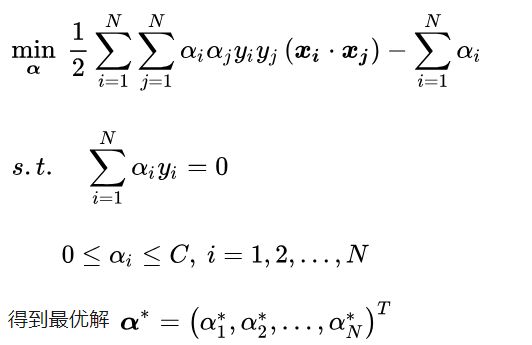
然后同样求解w和b：

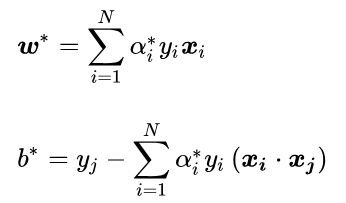
所以最后得到分隔超平面：

分类决策函数：

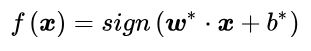
7 核函数

我们可能会碰到的一种情况是样本点不是线性可分的，比如：

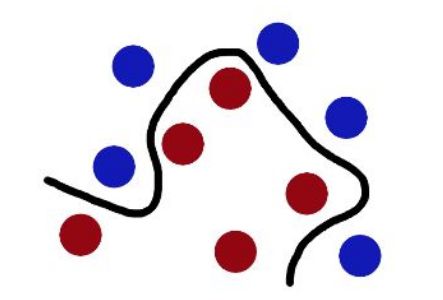
这种情况的解决方法就是：将二维线性不可分样本映射到高维空间中，让样本点在高维空间线性可分，比如：

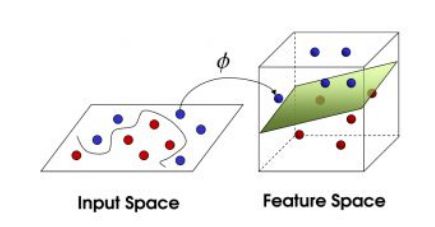
对于在有限维度向量空间中线性不可分的样本，我们将其映射到更高维度的向量空间里，再通过间隔最大化的方式，学习得到支持向量机，就是非线性 SVM。
因为低维空间映射到高维空间后维度可能会很大，如果将全部样本的点乘全部计算好，这样的计算量太大了。但如果我们有这样的一核函数K(x,z)=φ(x)·φ(z)，xi和xj在特征空间的内积等于它们在原始样本空间中通过函数 K(xi,xj)计算的结果，我们就不需要计算高维甚至无穷维空间的内积了。就是用核函数代替高维內积。
则求解步骤如下：
1.选取适当的核函数K(x,z)和惩罚参数C>0。构造并求解凸二次规划问题

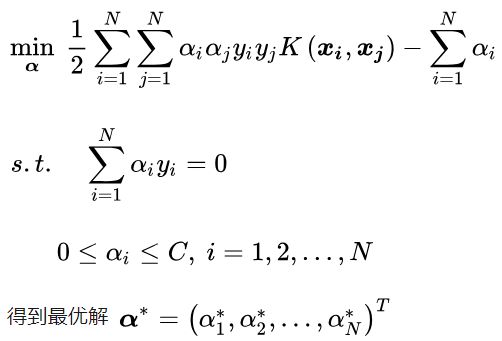
2.计算w和b
w与线性求解相同。
b求解如下：

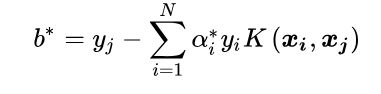
3.分类决策函数

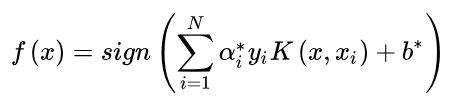
常见的核函数：
1.线性核函数

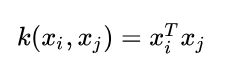
2.多项式核函数

3.高斯核函数

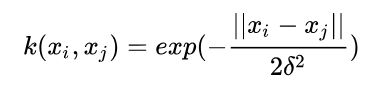
8 优缺点

优点

• 有严格的数学理论支持，可解释性强，不依靠统计方法，从而简化了通常的分类和回归问题
• 能找出对任务至关重要的关键样本（即：支持向量）
• 采用核技巧之后，可以处理非线性分类/回归任务
• 最终决策函数只由少数的支持向量所确定，计算的复杂性取决于支持向量的数目，而不是样本空间的维数，这在某种意义上避免了“维数灾难”

缺点

• 训练时间长。当采用 SMO 算法时，由于每次都需要挑选一对参数，因此时间复杂度为O(N) ，其中 N 为训练样本的数量
• 模型预测时，预测时间与支持向量的个数成正比。当支持向量的数量较大时，预测计算复杂度较高。

支持向量机目前只适合小批量样本的任务，无法适应百万甚至上亿样本的任务。

参考：
《统计学习方法》李航
支持向量机通俗导论（理解SVM的三层境界）：https://blog.csdn.net/macyang/article/details/38782399
支持向量机（SVM）——原理篇：https://zhuanlan.zhihu.com/p/31886934
【机器学习】支持向量机 SVM（非常详细）：https://zhuanlan.zhihu.com/p/77750026?utm_source=wechat_session
支持向量机原理篇之手撕线性SVM：https://cuijiahua.com/blog/2017/11/ml_8_svm_1.html
拉格朗日函数与广义拉格朗日函数：https://blog.csdn.net/LilyZJ/article/details/88778940