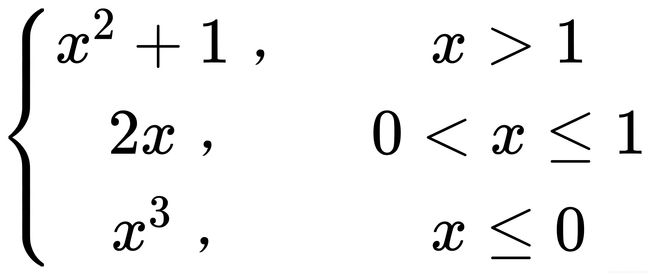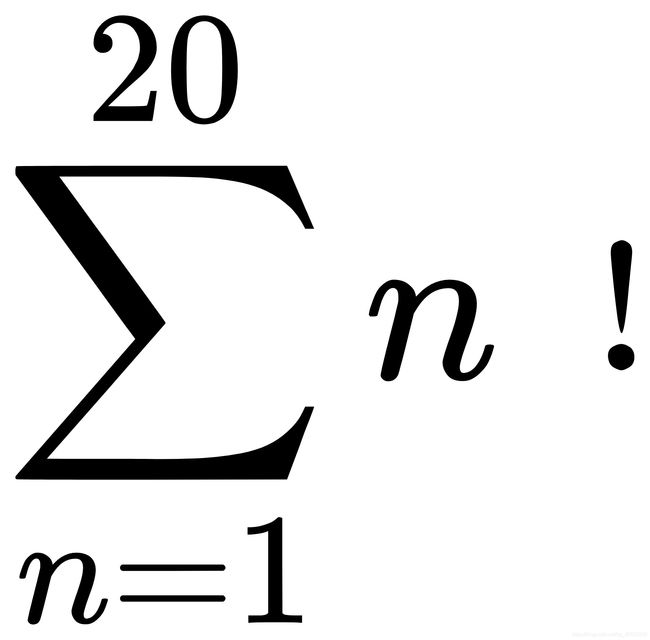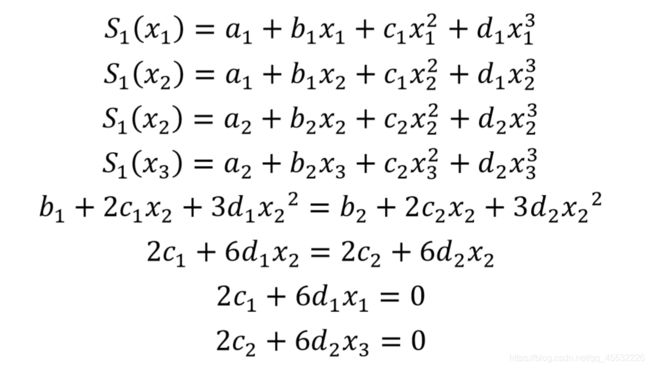【数学建模】数学建模课程总复习
一.MATLAB的使用及编程
1.填空知识点总结
(1)MATLAB中标点符号的含义:
- MATLAB每条命令后有逗号或无标点符号 —— 显示命令的结果
- MATLAB每条命令后为分号 —— 禁止显示命令结果
- % —— 所有文字为注释
- … —— 续行符
(2)数组的建立
- x = [ a b c d e ] —— 创建包含指定元素的行向量
- x = first:last —— 创建从first开始,加1计数,到last结束的行向量
- x = first:increment:last —— 从first开始,加increment计数,到last结束的行向量
- linspace(first,last,n) —— 从first开始,到last结束,有n个元素的行向量
(3)特殊的矩阵命令
- a = [ ] —— 产生一个空矩阵,当对一项操作无结果时,返回空矩阵,空矩阵大小为0
- b = zero(m,n) —— 产生一个m行n列的零矩阵
- c = ones(m,n) —— 产生一个m行n列的元素全为1的矩阵
- d = eye(m,n) —— 产生一个m行n列单位矩阵
(4)矩阵中元素的操作及运算
- A(i,:) —— 矩阵A的第i行
- A(:,j) —— 矩阵A 的第j列
- A( : ) —— 依次提取矩阵A的每一列,拉伸为一个列向量
- A(i1:i2,j1:j2) —— 取矩阵A的第i1-i2行、第j1-j2列构成新的矩阵
- A(i2: -1:i1,:) —— 依次提取矩阵的i1-i2行构成新矩阵
- A(:,j2: -1:j1) —— 依次提取矩阵的j1-j2列构成新矩阵
- A(i1:i2,:)=[ ] —— 删除矩阵的i1-i2行构成新矩阵
- A(:,j1:j2)=[ ] —— 删除矩阵的j1-j2列构成新矩阵
- [A B] or [A;B] —— 拼接矩阵A和B构成新矩阵
- A+B —— 矩阵的加法
- A*B ——矩阵的乘法
- det(A) —— 方阵的行列式
- inv(A) —— 方阵的逆
- [V,D] = eig(A) ——方阵的特征值与特征向量
(5)常用的画图函数
- plot(x,y) —— 绘制x关于y的曲线图
- ezplot(f) or fplot(f) —— 符号函数画图
- polar(theta,rho,S) —— 用角度theta和极半径rho作极坐标图,用S指定线型。
- plot3(x,y,z,S) —— 画三维曲线
- surf(X,Y,Z) —— 空间曲面
- mesh(X,Y,Z) —— 网格曲面
(6)处理图形
- gird on/off —— 增加/删除格栅
- xlabel() —— x轴标签
- ylabel() —— y轴标签
- title() —— 顶端标题
- gtext() —— 标注
- hold on/off 保持/关闭图像
(7)练习1:写出用linespace函数创建等间隔行向量设x=1:2:20的语句:x=linespace(1:19:10)
(8)练习2:设x=1:2:20写出以下表达式的值:
①x(1:3)的值为:[1,3,5]
②x(end-2:end)的值为:[15,17,19]
③length(x)的值为:10
④mean(x)的值为:10
(9)在matlab中输入以下语句:
>> clear;
x=1:2:20;
x(100)=100;
y=sum(x);
disp(y)
(1)执行以上程序后,x是长度为100的行向量
(2)执行以上程序后,y的值是200
注:y=((1+19)x10)/2+100=100+100=200
(10)设A=[1,2,3,4;5,6,7,8;9,10,11,12],写出以下表达式的值:
①A(end,:)的值为[9,10,11,12]
②A(:,[3,4])的值为[3,4;7,8;11,12]
③A(1,4)的值为4
④A(4)的值为2
注:对于A(i)来说,二维数组按列存取
⑤size(A)的值为[3,4]
注:size就是矩阵的行列大小
⑥sum(A)的值为[15,18,21,24]
注:sum和是将列进行加法计算存储在一个新的行向量里
⑦执行[m,n]=size(A)后,m=3,n=4
(11)设C={‘one’,‘two’,‘three’;zero(3),ones(2),eye(3)}
①size( C )的值为[2,3]
②C{1,1}的值为’one’
③length(C{1,1})的值为3
④C{2,2}的值为[1,1;1,1]
⑤C{2,3}的值为[1,0,0;0,1,0;0,0,1]
2.编程例题及练习题总结
例1.用for循环,对n=1,2,…,10,分别求xn=sin(nπ/10)
for n=1:10
x(n)=sin(n*pi/10)
end
x
例2.用while循环,设银行年利率为11.25%,将10000元存入银行,问多长时间会连本带利翻一番?
money = 10000;
years = 0;
while money<20000
years = years+1;
money = money*(1+11.25/100);
end
years
money
%函数fun2.m
function f = fun2(x)
if x>1
f = x^2+1;
elseif x<=0
f = x^3;
else
f = 2*x;
end
end
%在命令窗口输入fun2(2),fun2(0.5),fun2(-1)即可
练习1.用起泡法对10个数由小到大排序,即将相邻位置两个数字比较,将小的调到前头。
x=input('请输入10个数字构成的数组:');
for i=1:10
for j=1:10-i
if(x(j)>x(j+1))
temp=x(j);
x(j)=x(j+1);
x(j+1)=temp;
end
end
end
f=x
练习2.有一个4x5的矩阵,用编程求出其元素最大值所处的位置
x=input('请输入4x5矩阵');
max=-1;
flagi=0;
flagj=0;
for i=1:4
for j=1:5
if(x(i,j)>max)
max=x(i,j);
flagi=i;
flagj=j;
end
end
end
flagi,flagj
res=1;
i=1;
sum=0;
while(i<=20)
res=res*i;
i=i+1;
sum=sum+res;
end
sum
练习4.一球从100m高度自由下落,每次落地后反跳回原高度的一半,再落下,求它在第十次落地时共经过多少米,第10次反弹有多高?
h=100;
sum1=0;
for i=1:10
sum1=sum1+h;
h=0.5*h;
end
h11=0.5*h;%10次之后再反弹是原来的一半,还要再除一次2
sum1,h11
练习5.有一函数f(x,y)=x2+sinxy+2y,写一程序,输入自变量的值,输出函数值。
x=input("请输入x的值");
y=input("请输入y的值");
f=x^2+sin(x*y)+2*y;
f
练习6.求[100,200]之间第一个能被13整除的数
for i=100:200
if(mod(i,13)==0)
disp(i)
break;
end
end
练习7.一个数字各位数字的立方和等于这个数本身,则称该数为水仙花数,输出全部三位的水仙花数。
for i=100:999
baiwei=fix(i/100);
gewei=mod(i,10);
shiwei=(i-baiwei*100-gewei)/10;
if i==baiwei^3+shiwei^3+gewei^3
disp(i)
end
end
练习8.根据π2/6=1+1/22+…+1/n2求π的近似值,(n取1000)
sum=0;
for i=1:1000
sum=sum+1/i^2;
end
pai=sqrt(sum*6);
disp(pai)
二.动力系统模型
1.定义 数列A={a0,a1,a2…}的一阶差分是
△a0=a1-a0
△a1=a2-a1
…
对每个正整数n,第n个一阶差分是
△an=an+1-an
2.定理 动力系统an+1=ran+b,r≠1的平衡点是a=b/(1-r),如果r=1而b=0,那么每个数都是平衡点,如果r=1而b≠0,那么不存在平衡点:
| 动力系统an+1=ran+b,b≠0 | |
|---|---|
| r的值 | 所观察到的长期行为 |
| abs( r ) < 1 | 稳定平衡点 |
| abs( r )>1 | 不稳定平衡点 |
| r=1 | 没有平衡点,图形是一条直线 |
3.定理 对于某个依赖于初始条件常数c的动力系统an+1=ran+b,r≠1的解为ak=rkc+b/(1-r)
三.最小二乘法
1.直线拟合的正规方程:

2.拟合幂曲线

3.练习1 按给定模型用最小二乘法拟合数据
| x | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| y | 1 | 1 | 2 | 2 | 4 |
(1)y=ax+b
根据正规公式计算结果为:a=7/10,b=-1/10
(2)y=ax2
根据拟合幂曲线公式计算结果为:a=0.1596
四.低阶多项式的光滑化
1.寻求一个二次式,极小化偏差平方和,在数学上表示问题为:
2.存在极小点必要条件为:
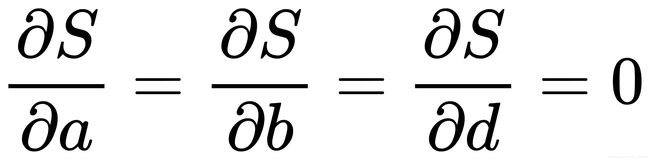
则可以产生下列方程
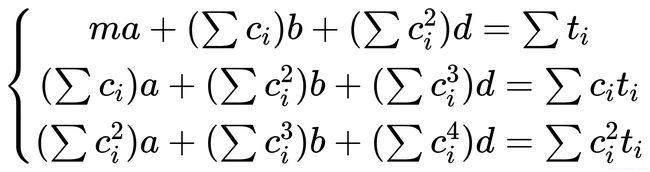
3.【带式录音带问题】解题思路:检查二阶均差(二阶导数)是常数,三阶导数为0,则可知利用二阶多项式进行光滑化,带入数据进入上述方程,即可求解。


五.自然样条
1.三阶样条不仅提供了在每一数据内部数据点斜率匹配的可能性,还提供了曲率的匹配。
同时还要求在每一内部数据点邻接的二阶导数匹配。
为了确定唯一常数,需要增加两个独立的方程,运用一阶导数是常数,二阶导数就必须是0这个条件,产生了自然样条的方程组:
六.随机数的生成
1.平均取中方法:
①从一个四位数x0开始称为种子
②将它平方得到一个八位数(必要时前面加0)
③取中间四位数作为下一个随机数
缺点:会退化为0并永远停在这里。
2.线性同余法:选择三个整数,给定某个初始种子,按照规则xn+1=(axn+b)mod©生成数列,其中,c是模,a是乘数,b是增量。
缺点:循环是在随机数中出现的主要问题,循环意味着序列自身的重复,它不可避免,所有伪随机数发生器都从循环开始。
例1 利用线性同余方法生成
(a)10个随机数,设a=5,b=1,c=8
(b)15个随机数,设a=1,b=7,c=10
(c)20个随机数,设a=5,b=3,c=16
(d)对上面得到的每个数列做出评论,存在循环吗?若存在,何时出现?
解:已知线性同余的规则是:xn+1=(axn+b)mod( c ),假设给定的初始种子是7
(a)
x1=(5×7+1)mod(8)=4
x2=(5×4+1)mod(8)=5
x3=(5×5+1)mod(8)=2
x4=(5×2+1)mod(8)=3
x5=(5×3+1)mod(8)=0
x6=(5×0+1)mod(8)=1
x7=(5×1+1)mod(8)=6
x8=(5×6+1)mod(8)=7
x9=(5×7+1)mod(8)=4
x10=(5×4+1)mod(8)=5
数列:4,5,2,3,0,1,6,7,……
(b)
x1=(1×7+7)mod(10)=4
x2=(1×4+7)mod(10)=1
x3=(1×1+7)mod(10)=8
x4=(1×8+7)mod(10)=5
x5=(1×5+7)mod(10)=2
x6=(1×2+7)mod(10)=9
x7=(1×9+7)mod(10)=6
x8=(1×6+7)mod(10)=3
x9=(1×3+7)mod(10)=0
x10=(1×0+7)mod(10)=7
x11=(1×7+7)mod(10)=4
x12=(1×4+7)mod(10)=1
x13=(1×1+7)mod(10)=8
x14=(1×8+7)mod(10)=5
x15=(1×5+7)mod(10)=2
数列:4,1,8,5,2,9,6,3,0,7,……
(c)
x1=(5×7+3)mod(16)=6
x2=(5×6+3)mod(16)=1
x3=(5×1+3)mod(16)=8
x4=(5×8+3)mod(16)=11
x5=(5×11+3)mod(16)=10
x6=(5×10+3)mod(16)=5
x7=(5×5+3)mod(16)=12
x8=(5×12+3)mod(16)=15
x9=(5×15+3)mod(16)=14
x10=(5×14+3)mod(16)=9
x11=(5×9+3)mod(16)=0
x12=(5×0+3)mod(16)=3
x13=(5×3+3)mod(16)=2
x14=(5×2+3)mod(16)=13
x15=(5×13+3)mod(16)=4
x16=(5×4+3)mod(16)=7
x17=(5×7+3)mod(16)=6
x18=(5×6+3)mod(16)=1
x19=(5×1+3)mod(16)=8
x20=(5×8+3)mod(16)=11
数列:6,1,8,11,10,5,12,15,14,9,0,3,2,13,4,7,……
(d)上面的每个数列都存在循环,在第c+1个数出现,每个循环中的数都包括0-(c-1)的所有整数。