matlab——plot函数大探索!这里有几乎关于plot的所有知识点
plot大探索
- 二维
- plot函数
- 一、plot函数的基本用法
- 函数调用:
- ==(1)plot(x,y):==
- ==(2)plot(x):==
- ==(3)plot(cx):==
- ==(4)plot(x,y):==
- ==(5)plot(x1,y1,x2,y2,x3,y3……xn,yn)==
- 例(1):
- 例(2):
- 例(4)1>:
- 例(5):
- 二、plot的选项
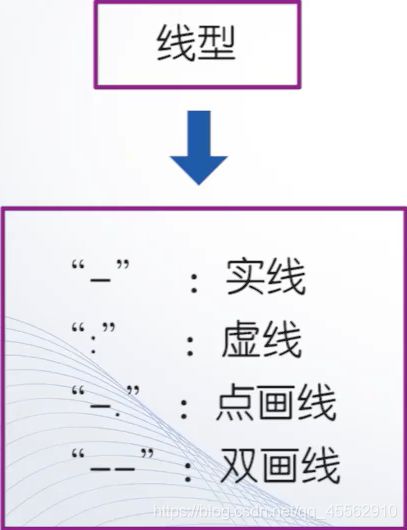
- 线型:
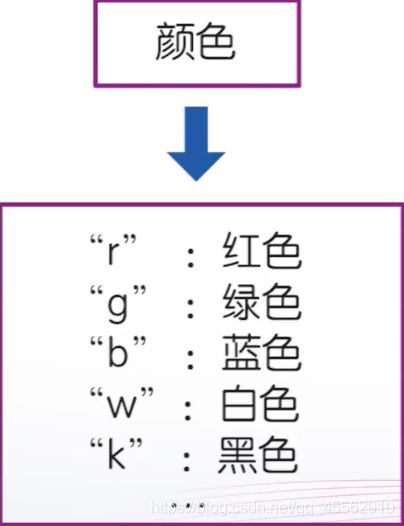
- 颜色
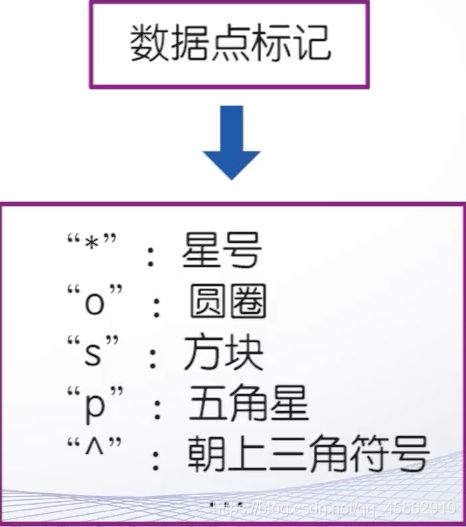
- 数据点标记
- 例子:
- fplot函数
- (1)基本用法
- ==fplot(f,lims,选项)==
- ==fplot(funx,funy,tlims,选项)==
- 三维绘图
- plot3函数
- fplot函数
二维
plot函数
一、plot函数的基本用法
函数调用:
(1)plot(x,y):
x存储横坐标,y存储纵坐标(x,y为向量时,长度相等)
(2)plot(x):
横坐标为i(下标),中坐标为x[i]
(3)plot(cx):
cx=x+y*i(x,y是实向量)是一个复向量,分别以该向量的实部和虚部为横纵坐标绘制曲线
(4)plot(x,y):
1>**当x是向量,y是矩阵时**:
如果y的列数=x的长度,则以x为横坐标,以y的每个行向量为纵坐标绘制曲线。 曲线条数等于y行数。
如果y的行数数=x的长度,则以x为横坐标,以y的每个列向量为纵坐标绘制曲线。 曲线条数等于y列数。
2>**当x,y为同型矩阵**
以x,y对应元素横纵坐标分别绘制曲线 ***曲线条数等于矩阵列数***
(5)plot(x1,y1,x2,y2,x3,y3……xn,yn)
含多个输入参数的plot函数。其中每一组向量对构成一个横纵坐标,n组向量对则绘制n条曲线
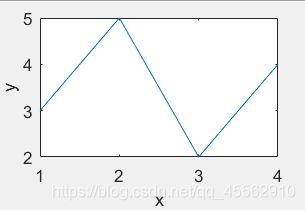
例(1):
x=[1 2 3 4];
y=[3 5 2 4];
plot(x,y);
xlabel('x');
ylabel('y');%表示坐标
%(1,3)(2,5)(3,2)(4,4)四个点用线段连接而形成的线。
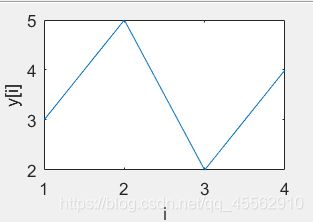
例(2):
y=[3 5 2 4];
plot(y);
xlabel('i');
ylabel('y[i]');
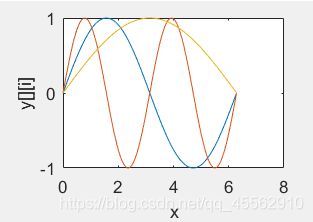
例(4)1>:
x=linspace(0,2*pi,100);%0~2*pi,元素个数为100
y=[sin(x);sin(2*x);sin(0.5*x)];%行向量长度与x相同0~2*pi,
plot(x,y);%曲线条数为y的列数。
xlabel('x');
ylabel('y[][i]');
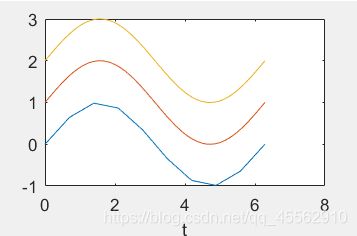
例(5):
t1=linspace(0,2*pi,10);
t2=linspace(0,2*pi,50);
t3=linspace(0,2*pi,100);%三者长度相同只是取点密度不同
plot(t1,sin(t1),t2,sin(t2)+1,t3,sin(t3)+2);
xlabel('t');
二、plot的选项
函数调用:
plot(x,y,选项)
线型:
颜色
数据点标记
例子:
%x=(0:pi/50:2*pi)';%是一个列向量,所以要转置
x=(linspace(0,2*pi,100))'
y1=2*exp(-0.5*x)*[1,-1];%exp:e;[1,-1]:分别存储两个包络线的纵坐标;y1是一个由两个列向量构成的矩阵
y2=2*exp(-0.5*x).*sin(2*pi*x);
x1=0:0.5:6;
%x1=linspace(0,6,13);%变化的时候要注意等差数列的元素个数
y3=2*exp(-0.5*x1).*sin(2*pi*x1);
plot(x,y1,'k:',x,y2,'b--',x1,y3,'rp');%用黑色虚线绘制两条包络线;蓝色双划线画y2;红色数据点标记为五角星
fplot函数
根据函数函数的变化特性,自适应 的设置采样间隔。函数变化缓慢时采样间隔大,函数值变化剧烈时采样间隔小
(1)基本用法
fplot(f,lims,选项)
- f:代表一个函数通常采用函数句柄形式
- lims:x轴的取值范围用二元向量表示[xmin,xmax],默认为[-5,5]。
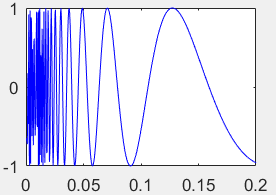
- 例
>> fplot(@(x)sin(1./x),[0,0.2],'b')
>@:定义句柄的运算符
fplot(funx,funy,tlims,选项)
双输入函数参数用法
- funx,funy代表函数,通常采用句柄形式。
- tlims:为以上参数函数的自变量取值范围。[tmin,tmax]
三维绘图
plot3函数
- plot(x,y,z)
情况一: x,y,z通常为长度相等的向量
情况二: x,y,z为同行矩阵时,则以对应列元素绘制曲线,曲线条数等于矩阵列数。
情况三: 当x,y,z中有向量也有矩阵时,行向量的长度必须与矩阵列数相同。列向量的长度与矩阵行数相同。
情况四: 含多组输入参数的plot3函数。
plot3(x1,y1,z1,x2,y2,z2,x3,y3,z3……xn,yn,zn);
每一组向量绘制一条曲线。
情况四: plot(x,y,z,选项)
下面是对应的一些例子。
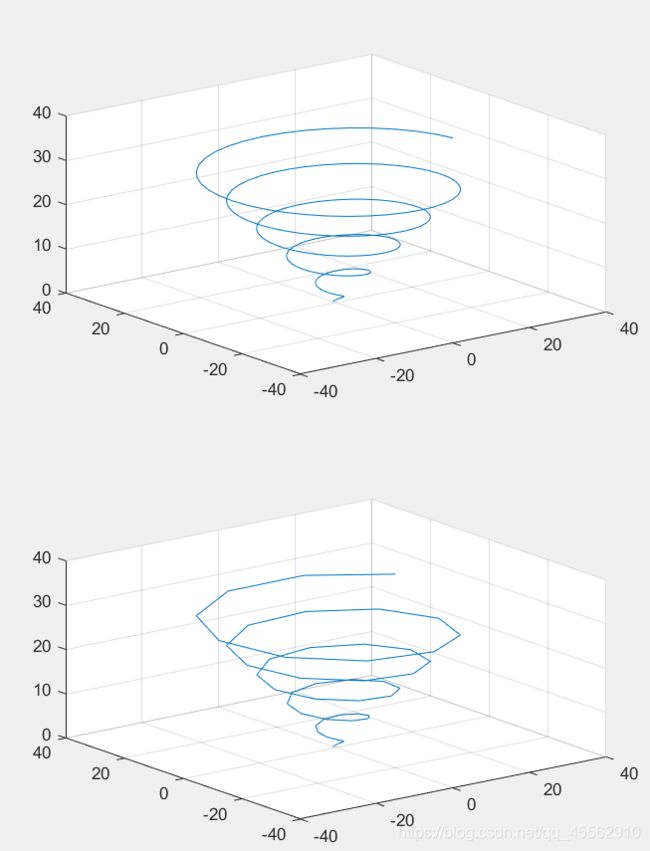
情况一:
t=linspace(0,10*pi,200);
x=sin(t)+t.*cos(t);
y=cos(t)-t.*sin(t);
z=t;
subplot(2,1,1);
plot3(x,y,z);
grid on
subplot(2,1,2);
plot3(x(1:4:200),y(1:4:200),z(1:4:200));%分别在x,y,z坐标中每隔4个点取一个点。所以看起来比较粗糙
grid on
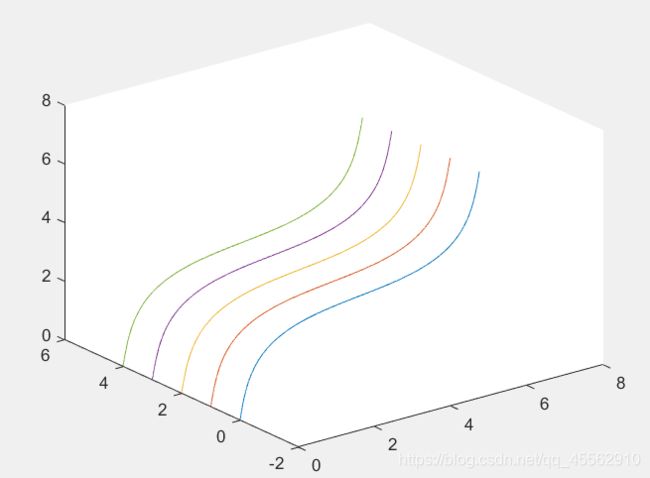
情况
t=0:0.001:2*pi;
t=t';%转置
x=[t,t,t,t,t];%写成x=t也行
y=[sin(t),sin(t)+1,sin(t)+2,sin(t)+3,sin(t)+4];
z=[t,t,t,t,t];
plot3(x,y,z);
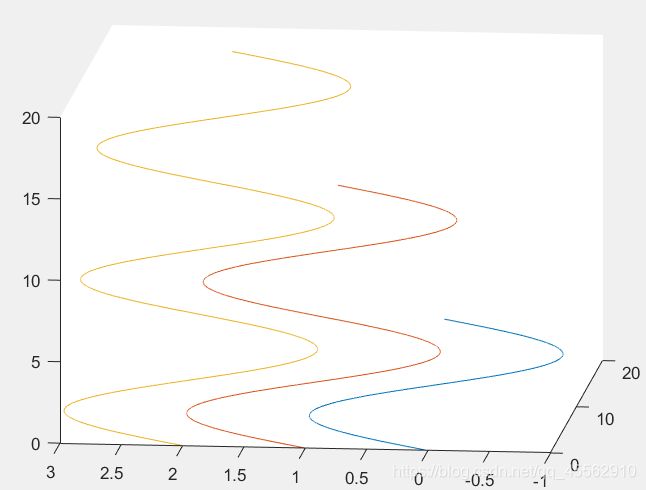
情况四:
t1=0:0.001:2*pi;
t2=0:0.001:4*pi;
t3=0:0.001:6*pi;
plot3(t1,sin(t1),t1,t2,sin(t2)+1,t2,t3,sin(t3)+2,t3);
fplot函数
- 调用格式:fplot(funx,funy,funz,tlims)
tlims:表示参数函数自变量的取值范围,用二元向量[tmin,tmax]描述,默认为[-5,5]
ps:因为版本原因,我并没有做出来,可以换更高版本的。(我的版本是2015b的)
%墨西哥帽顶曲线
xt=@(t)exp(-t/10).*sin(5*t);
yt=@(t)exp(-t/10).*cos(5*t);
zt=@(t)t;
fplot3(xt,yt,zt,[-12,12]);
使用句柄形式