约束规划——拉格朗日乘数法
拉格朗日乘数法
拉格朗日乘数法的基本思想
拉格朗日乘数法(Lagrange Multiplier Method)是一种优化算法,拉格朗日乘子法主要用于解决约束优化问题,它的基本思想就是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有(n+k)个变量的无约束优化问题。拉格朗日乘子背后的数学意义是其为约束方程梯度线性组合中每个向量的系数。
如何将一个含有n个变量和k个约束条件的约束优化问题转化为含有(n+k)个变量的无约束优化问题?拉格朗日乘数法从数学意义入手,通过引入拉格朗日乘子建立极值条件,对n个变量分别求偏导对应了n个方程,然后加上k个约束条件(对应k个拉格朗日乘子)一起构成包含了(n+k)变量的(n+k)个方程的方程组问题,这样就能根据求方程组的方法对其进行求解。
解决的问题模型为约束优化问题:
m i n / m a x f ( x , y , z ) min/max f(x,y,z) min/maxf(x,y,z)
s . t . s.t. s.t. g ( x , y , z ) = 0 g(x,y,z)=0 g(x,y,z)=0
数学实例
首先,我们先以麻省理工学院数学课程的一个实例来作为介绍拉格朗日乘数法的引子。求双曲线xy=3上离远点最近的点。
解:首先,我们根据问题的描述来提炼出问题对应的数学模型,即:
m i n f ( x , y ) = x 2 + y 2 min f(x,y)=x^2+y^2 minf(x,y)=x2+y2
s . t . s.t. s.t. x y = 3 xy=3 xy=3
(两点之间的欧氏距离应该还要进行开方,但是这并不影响最终的结果,所以进行了简化,去掉了平方)
根据上式我们可以知道这是一个典型的约束优化问题,其实我们在解这个问题时最简单的解法就是通过约束条件将其中的一个变量用另外一个变量进行替换,然后代入优化的函数就可以求出极值。我们在这里为了引出拉格朗日乘数法,所以我们采用拉格朗日乘数法的思想进行求解。
我们将 x 2 + y 2 = c x^2+y^2=c x2+y2=c的曲线族画出来,如下图所示,当曲线族中的圆与 x y = 3 xy=3 xy=3曲线进行相切时,切点到原点的距离最短。也就是说,当 f ( x , y ) = c f(x,y)=c f(x,y)=c的等高线和双曲线 g ( x , y ) g(x,y) g(x,y)相切时,我们可以得到上述优化问题的一个极值(注意:如果不进一步计算,在这里我们并不知道是极大值还是极小值)。
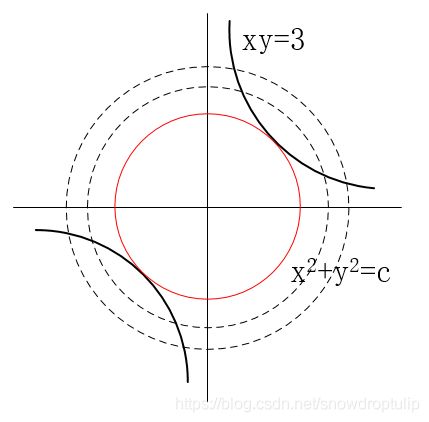
现在原问题可以转化为求当f(x,y)和g(x,y)相切时,x,y的值是多少?
如果两个曲线相切,那么它们的切线相同,即法向量是相互平行的: ▽ f / / ▽ g ▽f//▽g ▽f//▽g
由 ▽ f / / ▽ g ▽f//▽g ▽f//▽g可以得到, ▽ f = λ ▽ g ▽f=λ▽g ▽f=λ▽g。
这时,我们将原有的约束优化问题转化为了一种无约束的优化问题,如下所示:
原问题(约束优化问题):
m i n f ( x , y ) = x 2 + y 2 min f(x,y)=x^2+y^2 minf(x,y)=x2+y2
s . t . s.t. s.t. x y = 3 xy=3 xy=3
无约束方程组问题:
由 ▽ f / / ▽ g ▽f//▽g ▽f//▽g可以得到
∂ f ∂ x = λ ∂ g ∂ x \frac{\partial f}{\partial x} =λ \frac{\partial g}{\partial x} ∂x∂f=λ∂x∂g
∂ f ∂ y = λ ∂ g ∂ y \frac{\partial f}{\partial y} =λ \frac{\partial g}{\partial y} ∂y∂f=λ∂y∂g
x y = 3 xy=3 xy=3
通过求解上面的无约束方程组我们可以获取原问题的解:
2 x = λ y 2x=\lambda y 2x=λy
2 y = λ x 2y = \lambda x 2y=λx
x y = 3 xy=3 xy=3
通过求解上式可得, λ = 2 λ=2 λ=2或者是 − 2 -2 −2:
当 λ = 2 λ=2 λ=2时, ( x , y ) = ( 3 , 3 ) (x,y)=(\sqrt3, \sqrt3) (x,y)=(3,3)或者 ( − 3 , − 3 ) (-\sqrt3, -\sqrt3) (−3,−3),
当 λ = − 2 λ=-2 λ=−2时,无解。
所以原问题的解为 ( x , y ) = ( 3 , 3 ) (x,y)=(\sqrt3, \sqrt3) (x,y)=(3,3)或者 ( − 3 , − 3 ) (-\sqrt3, -\sqrt3) (−3,−3)。
通过举上述这个简单的例子就是为了体会拉格朗日乘数法的思想,即通过引入拉格朗日乘子 λ \lambda λ将原来的约束优化问题转化为无约束的方程组问题。
拉格朗日乘数法的基本形态
求函数 f ( x , y ) f(x,y) f(x,y)在满足 g ( x , y ) = c g(x,y)=c g(x,y)=c下的条件极值,可以转化为函数 L ( x , y , λ ) = f ( x , y ) + λ ( g ( x , y ) − c ) L(x,y,\lambda)=f(x,y)+\lambda (g(x,y)-c) L(x,y,λ)=f(x,y)+λ(g(x,y)−c)的无条件极值问题。
我们可以画图来辅助思考。
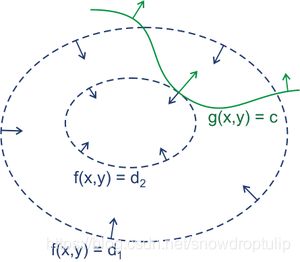
绿线标出的是约束g(x,y)=c的点的轨迹。蓝线是f(x,y)的等高线。箭头表示斜率,和等高线的法线平行。
从图上可以直观地看到在最优解处,f和g的斜率平行。
▽ [ f ( x , y ) + λ ( g ( x , y ) − c ) ] = 0 , λ ≠ 0 ▽[f(x,y)+λ(g(x,y)−c)]=0, λ≠0 ▽[f(x,y)+λ(g(x,y)−c)]=0,λ=0
一旦求出λ的值,将其套入下式,易求在无约束极值和极值所对应的点。
L ( x , y ) = f ( x , y ) + λ ( g ( x , y ) − c ) L(x,y)=f(x,y)+λ(g(x,y)−c) L(x,y)=f(x,y)+λ(g(x,y)−c)
新方程 F ( x , y ) F(x,y) F(x,y)在达到极值时与 f ( x , y ) f(x,y) f(x,y)相等,因为 L ( x , y ) L(x,y) L(x,y)达到极值时 g ( x , y ) − c g(x,y)−c g(x,y)−c总等于零。
例1
给定椭球 x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 a2x2+b2y2+c2z2=1,求这个椭球的内接长方体的最大体积。
这个问题实际上就是条件极值问题,即在条件 x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 a2x2+b2y2+c2z2=1下求 f ( x , y , z ) = 8 x y z f(x,y,z)= 8xyz f(x,y,z)=8xyz的最大值。
当然这个问题实际可以先根据条件消去 z z z,然后带入转化为无条件极值问题来处理。但是有时候这样做很困难,甚至是做不到的,这时候就需要用拉格朗日乘数法了。通过拉格朗日乘数法将问题转化为:
L ( x , y , z , λ ) = f ( x , y , z ) + λ g ( x , y , z ) = 8 x y z + λ ( x 2 a 2 + y 2 b 2 + z 2 c 2 − 1 ) L(x,y,z,\lambda)=f(x,y,z)+\lambda g(x,y,z)=8xyz+\lambda(\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}-1) L(x,y,z,λ)=f(x,y,z)+λg(x,y,z)=8xyz+λ(a2x2+b2y2+c2z2−1)
对 L ( x , y , z , λ ) L(x,y,z,\lambda) L(x,y,z,λ)求偏导:
∂ x L ( x , y , z , λ ) ∂ x = 8 y z + 2 λ x a 2 = 0 \frac{\partial xL(x,y,z,\lambda)}{\partial x} =8yz+\frac{2\lambda x}{a^2}=0 ∂x∂xL(x,y,z,λ)=8yz+a22λx=0
∂ x L ( x , y , z , λ ) ∂ y = 8 x z + 2 λ y b 2 = 0 \frac{\partial xL(x,y,z,\lambda)}{\partial y} =8xz+\frac{2\lambda y}{b^2}=0 ∂y∂xL(x,y,z,λ)=8xz+b22λy=0
∂ x L ( x , y , z , λ ) ∂ z = 8 x y + 2 λ z c 2 = 0 \frac{\partial xL(x,y,z,\lambda)}{\partial z} =8xy+\frac{2\lambda z}{c^2}=0 ∂z∂xL(x,y,z,λ)=8xy+c22λz=0
∂ x L ( x , y , z , λ ) ∂ λ = x 2 a 2 + y 2 b 2 + z 2 c 2 − 1 = 0 \frac{\partial xL(x,y,z,\lambda)}{\partial \lambda} =\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}-1=0 ∂λ∂xL(x,y,z,λ)=a2x2+b2y2+c2z2−1=0
最终得到 x = 3 3 a , y = 3 3 b , z = 3 3 c x=\frac{\sqrt 3}{3}a,y=\frac{\sqrt 3}{3}b,z=\frac{\sqrt 3}{3}c x=33a,y=33b,z=33c
最大体积为 V m a x = f ( 3 3 a , 3 3 b , 3 3 c ) = 8 3 9 a b c V_{max}=f(\frac{\sqrt 3}{3}a,\frac{\sqrt 3}{3}b,\frac{\sqrt 3}{3}c)=\frac{8\sqrt 3}{9}abc Vmax=f(33a,33b,33c)=983abc
多约束的拉格朗日乘数法
上面我们讨论的都是单约束的拉格朗日乘数法,当存在多个等式约束时(其实不等式约束也是一样的),我们进行一些推广:
m i n / m a x f ( x , y , z ) min/max f(x,y,z) min/maxf(x,y,z)
s . t . s.t. s.t. g i ( x , y , z ) = 0 , i = 1 , 2 , . . . , N g_i(x,y,z)=0, i = 1,2,...,N gi(x,y,z)=0,i=1,2,...,N
多约束拉格朗日乘数法的函数表达形式为:
L ( x , y , z , λ ) = f ( x , y , z ) + Σ i N λ i g i ( x , y , z ) L(x,y,z,\lambda)=f(x,y,z)+\Sigma_i^N\lambda_ig_i(x,y,z) L(x,y,z,λ)=f(x,y,z)+ΣiNλigi(x,y,z)
广义拉格朗日乘数法(Generalized Lagrange multipliers)
以上我们的拉格朗日乘数法解决了等式约束的最优化问题,但是在存在不等式的最优化问题,因此学者提出了广义拉格朗日乘数法,用与解决含有不等式约束的最优化问题。
首先,我们先一般化我们的问题:
m i n x , y , z f ( x , y ) min_{x,y,z}f(x,y) minx,y,zf(x,y)
s . t . s.t. s.t. g i ( x , y ) ≤ 0 , i = 1 , 2 , . . . , N g_i(x,y)\le0,i=1,2,...,N gi(x,y)≤0,i=1,2,...,N
h i ( x , y ) = 0 , i = 1 , 2 , . . . , M h_i(x,y)=0,i=1,2,...,M hi(x,y)=0,i=1,2,...,M
类似于拉格朗日乘数法,我们用 α i \alpha_i αi和 β i \beta_i βi作为不等式约束和等式约束的拉格朗日乘子,得出如下:
L ( x , y , α , β ) = f ( x , y ) + Σ i N α i g i ( x , y ) + Σ i M β i h i ( x , y ) L(x,y,\alpha,\beta)=f(x,y)+\Sigma_i^N\alpha_ig_i(x,y)+\Sigma_i^M\beta_ih_i(x,y) L(x,y,α,β)=f(x,y)+ΣiNαigi(x,y)+ΣiMβihi(x,y)
KKT
KKT条件(Karush–Kuhn–Tucker conditions)指出,当满足以下几个条件的时候,其解是问题最优解的候选解(摘自wikipedia)。
1、Stationarity(稳定性)
对于最小化问题就是:
▽ f ( x , y ) + Σ i N α i ▽ g i ( x , y ) + Σ i M β i ▽ h i ( x , y ) = 0 ▽f(x,y)+\Sigma_i^N\alpha_i▽g_i(x,y)+\Sigma_i^M\beta_i▽h_i(x,y)=0 ▽f(x,y)+ΣiNαi▽gi(x,y)+ΣiMβi▽hi(x,y)=0
对于最大化问题就是:
▽ f ( x , y ) − ( Σ i N α i ▽ g i ( x , y ) + Σ i M β i ▽ h i ( x , y ) ) = 0 ▽f(x,y)-(\Sigma_i^N\alpha_i▽g_i(x,y)+\Sigma_i^M\beta_i▽h_i(x,y))=0 ▽f(x,y)−(ΣiNαi▽gi(x,y)+ΣiMβi▽hi(x,y))=0
2、Primal feasibility(原始可行性)
g i ( x , y ) ≤ 0 , i = 1 , 2 , . . . , N g_i(x,y)\le0,i=1,2,...,N gi(x,y)≤0,i=1,2,...,N
h i ( x , y ) = 0 , i = 1 , 2 , . . . , M h_i(x,y)=0,i=1,2,...,M hi(x,y)=0,i=1,2,...,M
3、Dual feasibility(对偶可行性)
α i ≥ 0 , i = 1 , 2 , . . . , N \alpha_i\ge0,i=1,2,...,N αi≥0,i=1,2,...,N
4、Complementary slackness(互补松弛)
α i g i ( x , y ) = 0 , i = 1 , 2 , . . . , N \alpha_ig_i(x,y)=0,i=1,2,...,N αigi(x,y)=0,i=1,2,...,N
其中的Stationarity(稳定性)与我们的拉格朗日乘数法的含义是相同的,就是梯度共线的意思;而Primal feasibility(原始可行性)条件就是主要约束条件,自然是需要满足的;有趣的和值得注意的是Dual feasibility(对偶可行性)和Complementary slackness(互补松弛),接下来我们探讨下这两个条件,以及为什么不等式约束会多出这两个条件。
为了接下来的讨论方便,我们将N设为3,并且去掉等式约束,这样我们的最小化问题的广义拉格朗日函数就变成了:
L ( x , y , α , β ) = f ( x , y ) + Σ i 3 α i g i ( x , y ) L(x,y,\alpha,\beta)=f(x,y)+\Sigma_i^3\alpha_ig_i(x,y) L(x,y,α,β)=f(x,y)+Σi3αigi(x,y)
绘制出来的示意图如下所示:
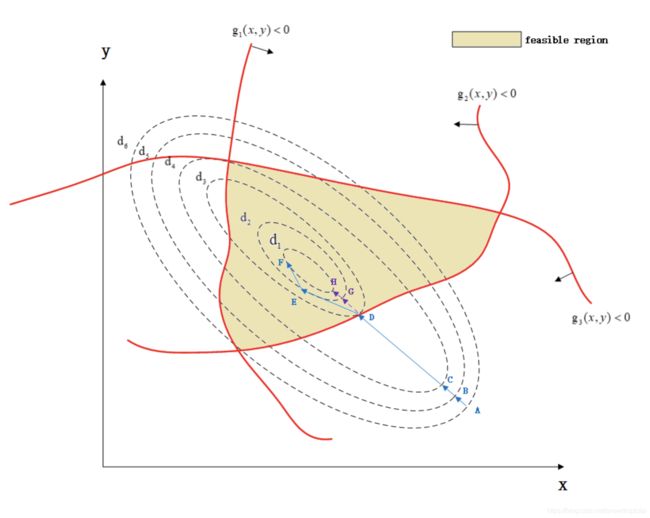
其中 d i > d j d_i>d_j di>dj,当 I > j I>j I>j,而蓝线为最优化寻路过程。
让我们仔细观察式子 α i ≥ 0 \alpha_i\ge0 αi≥0和 α i g i ( x , y ) = 0 \alpha_ig_i(x,y)=0 αigi(x,y)=0,我们不难发现,因为 α i ≤ 0 , g i ( x , y ) ≤ 0 \alpha_i\le0, g_i(x,y)\le0 αi≤0,gi(x,y)≤0,而 α i g i ( x , y ) = 0 \alpha_ig_i(x,y)=0 αigi(x,y)=0,所以 α i \alpha_i αi和 g i ( x , y ) g_i(x,y) gi(x,y)之中必有一个为0。
我们从上面的示意图入手理解并且记好公式 ▽ f ( x , y ) + Σ i N α i ▽ g i ( x , y ) + Σ i M β i ▽ h i ( x , y ) = 0 ▽f(x,y)+\Sigma_i^N\alpha_i▽g_i(x,y)+\Sigma_i^M\beta_i▽h_i(x,y)=0 ▽f(x,y)+ΣiNαi▽gi(x,y)+ΣiMβi▽hi(x,y)=0。
让我们假设初始化一个点A, 这个点A明显不处于最优点,也不在可行域内,可知 g 2 ( x , y ) > 0 g_2(x,y)>0 g2(x,y)>0,违背了 g i ( x , y ) ≤ 0 g_i(x,y)\le0 gi(x,y)≤0,为了满足约束 α i g i ( x , y ) = 0 \alpha_ig_i(x,y)=0 αigi(x,y)=0,有 α 2 = 0 \alpha_2=0 α2=0,导致 α i ▽ g i ( x , y ) = 0 \alpha_i▽g_i(x,y)=0 αi▽gi(x,y)=0
而对于 i = 1 , 3 i=1,3 i=1,3,因为满足约束条件而且 g 1 ( x , y ) ≠ 0 , g 3 ( x , y ) ≠ 0 g_1(x,y)≠0,g_3(x,y)≠0 g1(x,y)=0,g3(x,y)=0,所以 α 1 = 0 , α 3 = 0 \alpha_1=0,\alpha_3=0 α1=0,α3=0。这样我们的式子 ▽ f ( x , y ) + Σ i N α i ▽ g i ( x , y ) + Σ i M β i ▽ h i ( x , y ) = 0 ▽f(x,y)+\Sigma_i^N\alpha_i▽g_i(x,y)+\Sigma_i^M\beta_i▽h_i(x,y)=0 ▽f(x,y)+ΣiNαi▽gi(x,y)+ΣiMβi▽hi(x,y)=0就只剩下 ∇ f ( x , y ) ∇f(x,y) ∇f(x,y)
因此对着 ∇ f ( x , y ) ∇f(x,y) ∇f(x,y)进行优化,也就是沿着 f ( x , y ) f(x,y) f(x,y)梯度方向下降即可,不需考虑其他的条件(因为还完全处于可行域之外)。因此,A点一直走啊走,从A到B,从B到C,从C到D,这个时候因为D点满足 g 2 ( x , y ) = 0 g_2(x,y)=0 g2(x,y)=0,因此 α 2 > 0 \alpha_2>0 α2>0
,所以 α 2 ∇ g 2 ( x , y ) ≠ 0 \alpha_2∇g_2(x,y)≠0 α2∇g2(x,y)=0,因此 ▽ f ( x , y ) + Σ i N α i ▽ g i ( x , y ) + Σ i M β i ▽ h i ( x , y ) = 0 ▽f(x,y)+\Sigma_i^N\alpha_i▽g_i(x,y)+\Sigma_i^M\beta_i▽h_i(x,y)=0 ▽f(x,y)+ΣiNαi▽gi(x,y)+ΣiMβi▽hi(x,y)=0就变成了 ∇ f ( x , y ) + α 2 ∇ g 2 ( x , y ) ∇f(x,y)+\alpha_2∇g_2(x,y) ∇f(x,y)+α2∇g2(x,y)
所以在优化下一个点E的时候,就会考虑到需要满足约束 g 2 ( x , y ) ≤ 0 g_2(x,y)≤0 g2(x,y)≤0的条件,朝着向 g 2 ( x , y ) g_2(x,y) g2(x,y)减小,而且 f ( x , y ) f(x,y) f(x,y)减小的方向优化。因此下一个优化点就变成了E点,而不是G点。因此没有约束的情况下其优化路径可能是A→B→C→D→G→H,而添加了约束之后,其路径变成了A→B→C→D→E→F。
这就是为什么KKT条件引入了Dual feasibility(对偶可行性)和Complementary slackness(互补松弛),就是为了在满足不等式约束的情况下对目标函数进行优化。让我们记住这个条件,因为这个条件中某些 α i = 0 \alpha_i=0 αi=0的特殊性质,将会在SVM中广泛使用,而且正是这个性质定义了支持向量(SV)。
参考文献
最优化方法:拉格朗日乘数法
拉格朗日乘数法和KKT条件的直观解释