DesignTree算法实现与使用

目录

• 综述

• 案例

• 模型改进

• 应用

综述

    决策树算法在理解起来比较简单。因为操作单一，就是在不断的计算信息增益中递归的建树。为了阐述清楚这个算法的执行过程本文讲述通过一个简单的案例来阐述一下决策树算法的核心内容。并讨论一下如何提升。

案例

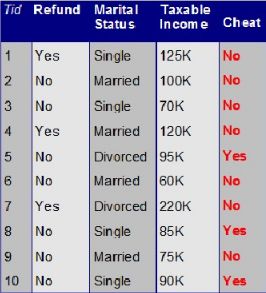
    从网上截取了一张案例图片，图片描述的是信用欺诈的案例，描述了三个特征分别是Refund、Marital Status、Teable InCome。接下来我们就一步步来完善决策树的构建过程。

    首先上信息熵的计算公式：

H(X)=−∑i=nNpilogpi H ( X ) = − ∑ i = n N p i log ⁡ p i

先来计算整体的信息熵定义为Bentropy。观察Cheat列，“No”的有7个，“Yes”的三个。此时： Bentropy=−710log710−310log310=0.88129 B e n t r o p y = − 7 10 log ⁡ 7 10 − 3 10 log ⁡ 3 10 = 0.88129 ；    下面计算每个特征的熵值：Refund特征中有Yes和No两个类别，类别概率分别为 Pyes=310,PNo=710 P y e s = 3 10 , P N o = 7 10 ，然后开始开始计算每一类中对应的结果标签（Cheat）中的值 ERefund=310(−1log1)+710(−37log37−47log47)=0.689659 E R e f u n d = 3 10 ( − 1 log ⁡ 1 ) + 7 10 ( − 3 7 log ⁡ 3 7 − 4 7 log ⁡ 4 7 ) = 0.689659 。因此可以得到第一个特征对用的信息增益InfoEntropy=0.88129-0.68966。然后对后面两个特征按照相同的办法求解信息增益。信息增益最大的当做根节点。
    1、信息增益最大的，表示熵最小的。熵最小纯度最高。这样把纯度高的好分的放在顶端。不好分的再往下分。提高正确性。2、当确定好根节点后，意味着数据集被分为了两个部分了，左子树部分和右子树部分。再次计算信息增益的时候要在子数据集中计算！

模型改进

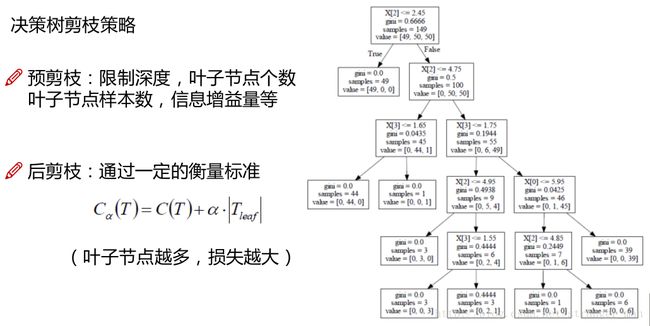
    按照前文所述的方法创建决策树存在一个大问题，当信息熵为0时，信息增益就达到最大了。但是信息熵为0时，只有一个叶节点。这个就存在一个只出现一个叶节点的情况。树的创建就进行不下去了。
    基于前面的讨论提出了信息增益比的方法，这样就使得信息熵不再为零的情况。先后提出了ID3、C4.5、CART等方法。决策数需要控制的参数比较多，但其泛化能力比较强还是好用的。、
    决策树简易版代码，请移步GITHUB

应用

决策树算法的使用、决策树可视化展示、决策树参数的自动化选择

%matplotlib inline

import matplotlib.pyplot as plt

import pandas as pd

from sklearn.datasets.california_housing import fetch_california_housing
housing = fetch_california_housing()
print(housing.DESCR)

downloading Cal. housing from http://www.dcc.fc.up.pt/~ltorgo/Regression/cal_housing.tgz to C:\Users\user\scikit_learn_data
California housing dataset.

The original database is available from StatLib

    http://lib.stat.cmu.edu/

The data contains 20,640 observations on 9 variables.

This dataset contains the average house value as target variable
and the following input variables (features): average income,
housing average age, average rooms, average bedrooms, population,
average occupation, latitude, and longitude in that order.

References
----------

Pace, R. Kelley and Ronald Barry, Sparse Spatial Autoregressions,
Statistics and Probability Letters, 33 (1997) 291-297.

housing.data.shape

(20640, 8)

housing.data[0]

array([   8.3252    ,   41.        ,    6.98412698,    1.02380952,
        322.        ,    2.55555556,   37.88      , -122.23      ])

from sklearn import tree
dtr = tree.DecisionTreeRegressor(max_depth = 2)
dtr.fit(housing.data[:, [6, 7]], housing.target)

DecisionTreeRegressor(criterion='mse', max_depth=2, max_features=None,
           max_leaf_nodes=None, min_impurity_split=1e-07,
           min_samples_leaf=1, min_samples_split=2,
           min_weight_fraction_leaf=0.0, presort=False, random_state=None,
           splitter='best')

#要可视化显示 首先需要安装 graphviz   http://www.graphviz.org/Download..php
dot_data = \
    tree.export_graphviz(
        dtr,
        out_file = None,
        # 自己做可视化的时候只需要改这个地方就可以啦
        feature_names = housing.feature_names[6:8],
        filled = True,
        impurity = False,
        rounded = True
    )

#pip install pydotplus
import pydotplus
graph = pydotplus.graph_from_dot_data(dot_data)
graph.get_nodes()[7].set_fillcolor("#FFF2DD")
from IPython.display import Image
Image(graph.create_png())

graph.write_png("dtr_white_background.png")

True

from sklearn.model_selection import train_test_split
data_train, data_test, target_train, target_test = \
    train_test_split(housing.data, housing.target, test_size = 0.1, random_state = 42)
dtr = tree.DecisionTreeRegressor(random_state = 42)
dtr.fit(data_train, target_train)

dtr.score(data_test, target_test)

0.637318351331017

from sklearn.ensemble import RandomForestRegressor
rfr = RandomForestRegressor( random_state = 42)
rfr.fit(data_train, target_train)
rfr.score(data_test, target_test)

0.79086492280964926

树模型参数:

• 1.criterion gini or entropy

• 2.splitter best or random 前者是在所有特征中找最好的切分点 后者是在部分特征中（数据量大的时候）

• 3.max_features None（所有），log2，sqrt，N 特征小于50的时候一般使用所有的

• 4.max_depth 数据少或者特征少的时候可以不管这个值，如果模型样本量多，特征也多的情况下，可以尝试限制下

• 5.min_samples_split 如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。

• 6.min_samples_leaf 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝，如果样本量不大，不需要管这个值，大些如10W可是尝试下5

• 7.min_weight_fraction_leaf 这个值限制了叶子节点所有样本权重和的最小值，如果小于这个值，则会和兄弟节点一起被剪枝默认是0，就是不考虑权重问题。一般来说，如果我们有较多样本有缺失值，或者分类树样本的分布类别偏差很大，就会引入样本权重，这时我们就要注意这个值了。

• 8.max_leaf_nodes 通过限制最大叶子节点数，可以防止过拟合，默认是”None”，即不限制最大的叶子节点数。如果加了限制，算法会建立在最大叶子节点数内最优的决策树。如果特征不多，可以不考虑这个值，但是如果特征分成多的话，可以加以限制具体的值可以通过交叉验证得到。

• 9.class_weight 指定样本各类别的的权重，主要是为了防止训练集某些类别的样本过多导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重如果使用“balanced”，则算法会自己计算权重，样本量少的类别所对应的样本权重会高。

• 10.min_impurity_split 这个值限制了决策树的增长，如果某节点的不纯度(基尼系数，信息增益，均方差，绝对差)小于这个阈值则该节点不再生成子节点。即为叶子节点 。

• n_estimators:要建立树的个数

from sklearn.grid_search import GridSearchCV
tree_param_grid = { 'min_samples_split': list((3,6,9)),'n_estimators':list((10,50,100))}
grid = GridSearchCV(RandomForestRegressor(),param_grid=tree_param_grid, cv=5)
grid.fit(data_train, target_train)
grid.grid_scores_, grid.best_params_, grid.best_score_

([mean: 0.78405, std: 0.00505, params: {'min_samples_split': 3, 'n_estimators': 10},
  mean: 0.80529, std: 0.00448, params: {'min_samples_split': 3, 'n_estimators': 50},
  mean: 0.80673, std: 0.00433, params: {'min_samples_split': 3, 'n_estimators': 100},
  mean: 0.79016, std: 0.00124, params: {'min_samples_split': 6, 'n_estimators': 10},
  mean: 0.80496, std: 0.00491, params: {'min_samples_split': 6, 'n_estimators': 50},
  mean: 0.80671, std: 0.00408, params: {'min_samples_split': 6, 'n_estimators': 100},
  mean: 0.78747, std: 0.00341, params: {'min_samples_split': 9, 'n_estimators': 10},
  mean: 0.80481, std: 0.00322, params: {'min_samples_split': 9, 'n_estimators': 50},
  mean: 0.80603, std: 0.00437, params: {'min_samples_split': 9, 'n_estimators': 100}],
 {'min_samples_split': 3, 'n_estimators': 100},
 0.8067250881273065)

rfr = RandomForestRegressor( min_samples_split=3,n_estimators = 100,random_state = 42)
rfr.fit(data_train, target_train)
rfr.score(data_test, target_test)

0.80908290496531576

pd.Series(rfr.feature_importances_, index = housing.feature_names).sort_values(ascending = False)

MedInc        0.524257
AveOccup      0.137947
Latitude      0.090622
Longitude     0.089414
HouseAge      0.053970
AveRooms      0.044443
Population    0.030263
AveBedrms     0.029084
dtype: float64