模拟退火算法解多元函数

模拟退火算法解多元函数

题目：
$F(x)=11.16386-0.0903x_1-0.1487x_2-0.0664x_3+0.09074x_4-2.452\ast 10^{-4}{x}_1{x}_2+6.228\ast 10^{-5}{x}_1{x}_3+2.457\ast 10^{-3}{x}_1{x}_4+3.8688\ast 10^{-3}{x}_2{x}_3-6.471\ast 10^{-3}{x}_2{x}_4-1.451\ast 10^{-3}{x}_3{x}_4$

约束条件：

$36.163<x_1<65.0934$

$0.45<1-\frac{3x_2}{2x_1}<0.5$

$12.0543<x_2<21.699$

$27.75<x_3<36.075$

$10<x_4-2x_3$

$x_4-3.2x_3<16$

$48.02<x_4$

求多目标函数$F(x)$的最小值？

资源链接

https://download.csdn.net/download/u013095333/12585474

解法1：暴力解法

思路，设置$x_1,x_2,x_3,x_4$的范围和精度，依次计算每一个$F(x)$的值，取最小的$F(x)$对应的$x_1,x_2,x_3,x_4$

#include 
using namespace std;

double f(double x1, double x2, double x3, double x4){
	double ans = 0;
	ans = 11.16386 - 0.0903*x1 - 0.1487*x2 - 0.0664*x3 + 0.0907*x4;
	ans = ans - 2.452*0.0001*x1*x2;
	ans = ans + 6.228*0.00001*x1*x3;
	ans = ans + 2.457*0.001*x1*x4;
	ans = ans + 3.8688*0.001*x2*x3;
	ans = ans - 6.471*0.001*x2*x4;
	ans = ans - 1.451*0.001*x3*x4;
	return ans;
}

int main()
{
	double x1, x2, x3, x4;
	double step = 1;
	x1 = 36.16;
	x2 = 12.05;
	x3 = 27.75;
	x4 = 48.02;
	double ftemp = 10000, x1temp = x1, x2temp = x2, x3temp = x3, x4temp = x4;
	while(x1 < 65.10){
		x2 = 12.05;
		while(x2 < 21.7){
			x3 = 27.75;
			while(x3 < 36.10){
				x4 = 48.02;
				while(x4 < 1000){
					double fx = 10000;
					double a = 1 - 3*x2/1.0/(2*x1);
					double b = x4 - 2*x3;
					double c = x4 - 3.2*x3;
					if(a>0.45&&a<0.5&&b>10&&c<16){
						fx = f(x1, x2, x3, x4);
					}
					if(ftemp > fx){
						ftemp = fx;
						x1temp = x1;
						x2temp = x2;
						x3temp = x3;
						x4temp = x4;
					}
					x4 = x4 + step;
				}
				x3 = x3 + step;
				cout << ftemp << " " << x1 << " " << x2 << " " << x3 << endl;
			}
			x2 = x2 + step;
		}
		x1 = x1 + step;
	}
	cout << ftemp << endl;
	cout << x1temp << " " << x2temp << " " << x3temp << " " << x4temp << endl;
	
	return 0;
} 

结果：

解法2：模拟退火

参考：
模拟退火算法
用模拟退火算法求解带约束的二元函数极值问题（Java实现）

#include 
using namespace std;

double f(double x1, double x2, double x3, double x4){
	double ans = 0;
	ans = 11.16386 - 0.0903*x1 - 0.1487*x2 - 0.0664*x3 + 0.0907*x4;
	ans = ans - 2.452*0.0001*x1*x2;
	ans = ans + 6.228*0.00001*x1*x3;
	ans = ans + 2.457*0.001*x1*x4;
	ans = ans + 3.8688*0.001*x2*x3;
	ans = ans - 6.471*0.001*x2*x4;
	ans = ans - 1.451*0.001*x3*x4;
	return ans;
}

double getRandom(){                       // 获取-1到1区间的随机数 
	return (rand()%200 - 100)/100.0;
}

double getRangeRandom(double a, double b){  // 获取a到b范围内的随机数 
	int step = (a-b)*1000;
	return rand()%step/1000.0+a; 
}


int main()
{
	srand((int)time(0));
	double T = 100, t = 100;
	double T_min = 1e-8;
	double step = 0.99;
	int k = 10;

	double x1[k], x2[k], x3[k], x4[k];
	double x1_min = 36.16;
	double x1_max = 65.10;
	double x2_min = 12.05;
	double x2_max = 21.7;
	double x3_min = 27.75;
	double x3_max = 36.10;
	double x4_min = 48.02;
	double x4_max = 100;
	double ftemp = 10000, ftemp_new, x1temp, x2temp, x3temp, x4temp;
	
	// 随机化初始值
	for(int i = 0; i < k; i++){
		x1[i] = getRangeRandom(x1_min, x1_max);
		x2[i] = getRangeRandom(x2_min, x2_max);
		x3[i] = getRangeRandom(x3_min, x3_max);
		x4[i] = getRangeRandom(x4_min, x4_max);
		double a = 1 - 3*x2[i]/1.0/(2*x1[i]);
		double b = x4[i] - 2*x3[i];
		double c = x4[i] - 3.2*x3[i];
		if(!(a>0.45&&a<0.5&&b>10&&c<16)){
			i--;
		}
	} 
	
	// 模拟退火 
	int time = 0;
	while(t > T_min){ 
		for(int i = 0; i < k; i++){
			ftemp = f(x1[i], x2[i], x3[i], x4[i]);
			// 在领域内产生新的解 
			double x1_new = x1[i] + getRandom();
			double x2_new = x2[i] + getRandom();
			double x3_new = x3[i] + getRandom();
			double x4_new = x4[i] + getRandom();
			double a = 1 - 3*x2_new/1.0/(2*x1_new);
			double b = x4_new - 2*x3_new;
			double c = x4_new - 3.2*x3_new;
			if(x1_new>x1_min&&x1_new<x1_max&&\
				x2_new>x2_min&&x2_new<x2_max&&\
				x3_new>x3_min&&x3_new<x3_max&&\
				x4_new>x4_min&&x4_new<x4_max&&\
				a>0.45&&a<0.5&&b>10&&c<16){
				ftemp_new = f(x1_new, x2_new, x3_new, x4_new);
				if(ftemp_new < ftemp){   // 有优化，直接替换
					x1[i] = x1_new;
					x2[i] = x2_new;
					x3[i] = x3_new;
					x4[i] = x4_new;
				}
				else{                   // 无优化，以一定概率接受较差的结果 
					if((t - T_min) > (rand()%100)){
						x1[i] = x1_new;
						x2[i] = x2_new;
						x3[i] = x3_new;
						x4[i] = x4_new;
					}
				} 
			}
		}
		t = t * step;
		// 输出每一轮迭代得到的最小值
		ftemp = 10000;
		for(int i = 0; i < k; i++){
			ftemp_new = f(x1[i], x2[i], x3[i], x4[i]);
			if(ftemp_new < ftemp){
				ftemp = ftemp_new;
				x1temp = x1[i];
				x2temp = x2[i];
				x3temp = x3[i];
				x4temp = x4[i];
			}
		} 
		if(time%100==0){
			cout << time << endl;
			cout << ftemp << endl;
			cout << x1temp << " " << x2temp << " " << x3temp << " " << x4temp << endl << endl; 
		}
		time++;
	}
	
	// 取k个中最小的
	ftemp = 10000;
	for(int i = 0; i < k; i++){
		ftemp_new = f(x1[i], x2[i], x3[i], x4[i]);
		if(ftemp_new < ftemp){
			ftemp = ftemp_new;
			x1temp = x1[i];
			x2temp = x2[i];
			x3temp = x3[i];
			x4temp = x4[i];
		}
	} 
	cout << "ans: " << endl;
	cout << ftemp << endl;
	cout << x1temp << " " << x2temp << " " << x3temp << " " << x4temp << endl;
	
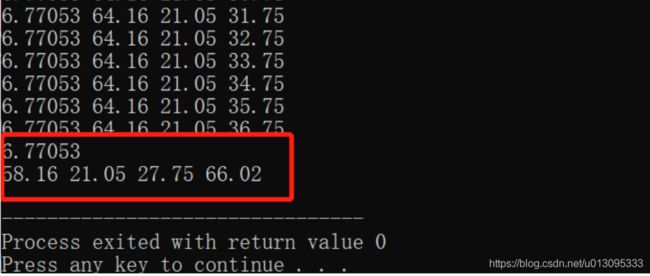
	return 0;
} 

结果：

与暴力解法得到的基本一致，说明该附近确为最小值对应的解

特点：速度比暴力算法快太多了，确实有用。

迭代过程图：

绘图代码：

import os
import numpy as np
import matplotlib.pyplot as plt

i = 0
time = []
fx = []
x1 = []
x2 = []
x3 = []
x4 = []
with open('out.txt', 'r') as file:
    context = file.read()
    context = context.split()
    for i in range(len(context)):
        if(i%6==0):
            time.append(int(context[i]))
        if(i%6==1):
            fx.append(float(context[i]))
        if(i%6==2):
            x1.append(float(context[i]))
        if(i%6==3):
            x2.append(float(context[i]))
        if(i%6==4):
            x3.append(float(context[i]))
        if(i%6==5):
            x4.append(float(context[i]))
        i = i + 1
        
# 数据清洗干净，下面绘图
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
plt.rcParams['axes.unicode_minus']=False

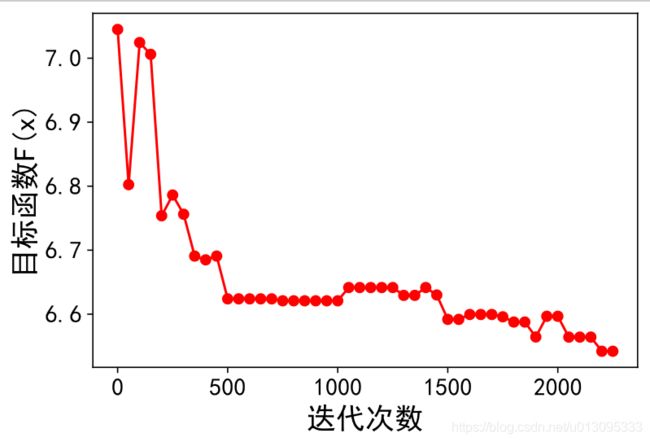
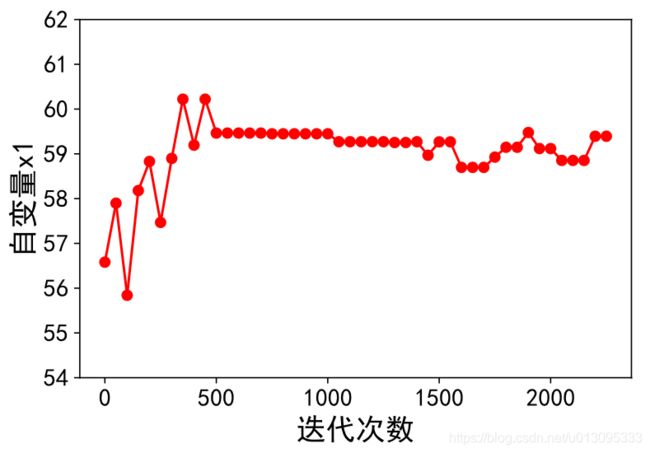
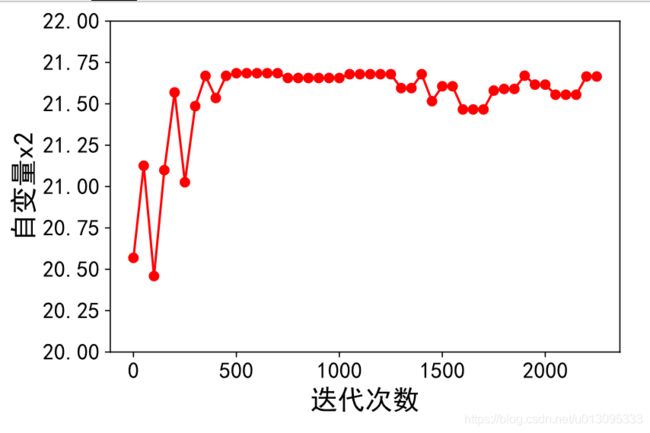
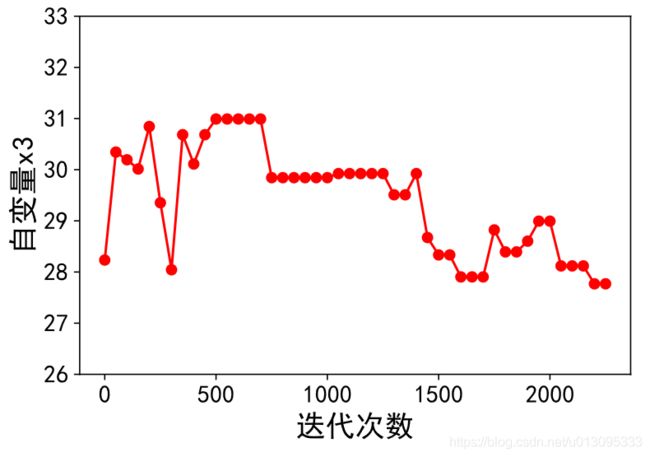
plt.plot(time, fx, marker = 'o', c = 'r', label = 'a=0.3')
plt.xlabel('迭代次数', fontsize = 18)
plt.ylabel('目标函数F(x)', fontsize = 18)
plt.xticks(fontsize = 15)
plt.yticks(fontsize = 15)
plt.savefig("fx.svg",bbox_inches='tight')