公式
《组合数学》里是这样写的:1
\[X_n=\{ 1,2, \dots ,n \}\]
\[F: \mathcal{P}(X_n) \rightarrow \Re\]
\[G: \mathcal{P}(X_n) \rightarrow \Re\]
白话:\(F\),\(G\) 都是一个函数,表示每个\(X_n\)的子集对应一个实数。$\mathcal{P}(X_n) $表示全体子集的集合。(数学表达抽象是为了针对普遍情况,可以带入具体的概念去理解)
其中
\[ G(K)=\sum\limits_{L \subseteq K }^{} F(L) \ (K \subseteq X_n)\]
特别地(通过莫比乌斯反演),我们有
\[ F(K)=\sum\limits_{L \subseteq K }^{} (-1)^{|K|-|L|}G(L) \ (K \subseteq X_n)\]
举例
《组合数学》书本例子2:(原文真的很讲究)设\(A_1,A_2,\dots,A_n\) 有限集\(S\) 的子集,\(K\subseteq \{1,2,\dots,n\}\)。
定义\(F(K)\)表示计数\(S\)里有多少个元素,不属于所有\(K\)选中的子集,而且都属于没选中的子集。
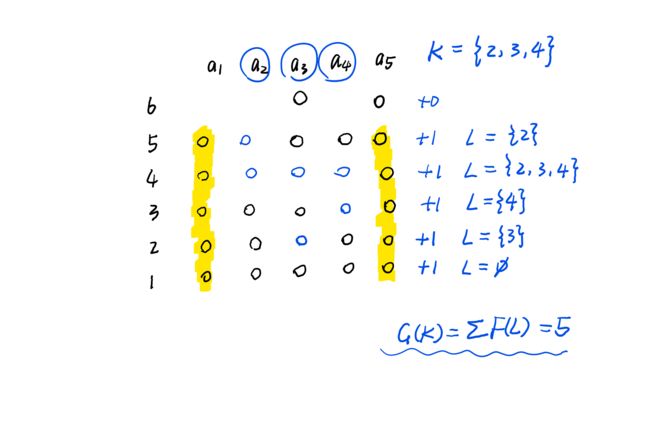
于是\(G(K)=\sum\limits_{L \subseteq K }^{} F(L) \) 就表示计数所有不在\(K\)选中的子集中的的共有元素的个数。要想通这一点有点不直接,可以画个图:(小黑圈表示有这个元素,小蓝圈表示没有。)
也可以这样想,所有不在\(K\)选中的子集中的的共有元素,是每个\(F(L)\)都会计一次的。知道了这一结论,可以发现\(G(K)\) 还是蛮好算的,有
\[G(K) = \left| \bigcap\limits_{i \notin K }^{} A_i \right| \]
根据反演公式,有
\[ F(K)=\sum\limits_{L \subseteq K }^{} (-1)^{|K|-|L|}G(L) \]
可以把集合表达式带进去,得到
\[\left| \overline{A_1} \cap \overline{A_2} \cap \dots \cap \overline{A_n} \right| =\sum\limits_{L \subseteq K }^{} (-1)^{|K|-|L|} \left| \bigcap\limits_{i \notin K }^{} A_i \right| \]
在等价替换一下,当\(K= \{1,2,\dots,n\}\)时,
\[\left| \overline{A_1} \cap \overline{A_2} \cap \dots \cap \overline{A_n} \right| =\sum\limits_{J \subseteq X_n }^{} (-1)^{|J|} \left| \bigcap\limits_{i \in J }^{} A_i \right| \]
这就等价容斥原理(绝了)。
理解可以这样: $\left| \overline{A_1 \cup A_2 \cup \dots \cup A_n} \right| $表示这些子集的并集,取反的元素还有多少个,这个问题容易想到是用容斥解,不过本文是为了引入莫比乌斯反演,表现一下容斥和莫比乌斯反演的关系。
我不想把篇幅弄得太长,太长不太便于阅读,下一篇将正式讲莫比乌斯反演的一些例子。
《组合数学》P115↩
《组合数学》P115↩