决策树(Decision Tree)算法原理总结(一)
如同上几篇我们探讨的SVM一样,决策树算法既可以处理分类问题(二分类和多分类),又可以处理回归问题。同时,决策树也广泛的运用在集成算法中,比如随机森林算法。本篇我们沿着决策树算法的发展,来探讨下决策树ID3算法和C4.5算法。CART算法决策树我们下篇单独再探讨。
1)来自借钱的思考
决策树的原理其实很简单,我们生活中已经在运用这些原理。比如,某一个朋友向你借钱,在你心里一定会有一系列的决策,最后决定是否借钱给他,把你的决策画成一颗树状结构就是决策树了。比如我的借钱决策:

从上图我们先来认识下决策树的基本结构,决策树由节点(矩形和椭圆)和有向的边(箭头)组成,节点按所处在决策树的位置可以分为根节点,中间节点和叶子节点。其中每个节点代表一个属性,每个分支代表一个决策(规则),每个叶子代表一个结果(分类值或连续值)。
再回到借钱的栗子上来。假如按照上面的决策树进行借钱决策,一共外借了4次钱,结果有2次按时还了钱,另外2次借的钱打水漂了,损失有点大。于是我调整了下策略,把是否有工作放在首要位置(跟节点)。决策树的结构如下: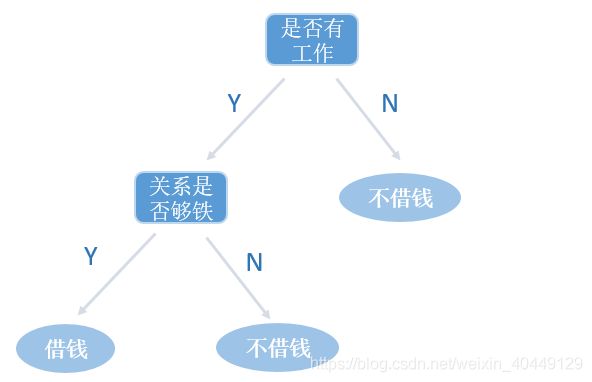
于是我又外借了4次钱,结果有3次按时还了钱,只有1次外借的钱打了水漂。对比第一种策略,不还钱的次数减少了,也可以说打水漂的不确定性减少了。所以,只要不确定性有所降低,我们的决策树就有所优化。那么,不确定性又该怎么去度量呢?幸运的是,早在1948年克劳德·爱尔伍德·香农提出了信息熵的概念,专门用来描述事物的不确定性。
2)信息熵(Information Entropy)
信息熵,它是表示对随机变量不确定的度量,不确定性越大,信息熵越大。随机变量 x x x的信息熵的表达式如下(信息熵表达式的由来可参考本篇博客信息熵部分):
H ( x ) = − ∑ x p ( x ) l o g ( p ( x ) ) = − ∑ i = 1 n p ( x i ) l o g p ( x i ) H(x) = -\sum_{x}p(x)log(p(x))=-\sum_{i=1}^{n}p(x_i)logp(x_i) H(x)=−∑xp(x)log(p(x))=−∑i=1np(xi)logp(xi)
从表达式中可以看出,随机变量的取值个数越多,状态数也就越多,信息熵就越大,混乱程度就越大。当随机分布为均匀分布时,信息熵最大。
再让我们回到栗子中来。只要不确定性减少,决策策略就得到了优化。因此我们在进行特征选择时,可以选择当前不确定性减少最多的特征(贪心法)。那么该怎么去定义不确定性的减少呢?ID3算法使用信息增益,C4.5使用信息增益率,CART树使用Gini系数。
3)ID3算法
ID3算法是用信息增益来定义不确定性的减少程度,选择信息增益最大的特征来建立决策树的当前节点。特征A对训练集D的信息增益 g ( D , A ) g(D,A) g(D,A)表达式如下:
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A)=H(D)-H(D|A) g(D,A)=H(D)−H(D∣A)
信息增益具体的算法过程:
输入:训练数据集D合特征A;
输出:特征A对训练数据集D的信息增益 g ( D , A ) g(D,A) g(D,A)
a)计算数据D的信息熵 H ( D ) H(D) H(D)
H ( D ) = − ∑ k = 1 K C k D l o g 2 C k D H(D)=-\sum _{k=1}^K\frac{C_k}{D}log_2\frac{C_k}{D} H(D)=−∑k=1KDCklog2DCk
b)计算特征A对数据集D的条件熵 H ( D ∣ A ) H(D|A) H(D∣A)(条件熵概念可以参考本篇博客)
H ( D ∣ A ) = − ∑ i = 1 n D i D H ( D i ) = − ∑ i = 1 n D i D ∑ k = 1 K D i k D i l o g 2 D i k D i H(D|A)=-\sum _{i=1}^n\frac{D_i}{D}H(D_i)=-\sum _{i=1}^n\frac{D_i}{D}\sum _{k=1}^K\frac{D_{ik}}{D_i}log_2\frac{D_{ik}}{D_i} H(D∣A)=−∑i=1nDDiH(Di)=−∑i=1nDDi∑k=1KDiDiklog2DiDik
c)计算信息增益
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A)=H(D)-H(D|A) g(D,A)=H(D)−H(D∣A)
下面我们来看看ID3的生成算法:
输入:训练数据集D,特征集A,阈值 ε \varepsilon ε;
输出:决策树T
a)初始化信息增益的阈值 ε \varepsilon ε;
b)若D中所有实例属于同一类 C k C_k Ck,则T为单节点树。标记类别为 C k C_k Ck,返回T;
c)若 A A A为空,则T为单节点树,将D中实例数最大的类 C k C_k Ck作为该节点的 类标记,返回T;
d)否则,计算A中各特征对D的信息增益,选择信息增益最大的特征 A g A_g Ag;
e)如果 A g A_g Ag的信息增益小于阈值 ε \varepsilon ε,则返回单节点树T,将D中实例数最大的类 C k C_k Ck作为该节点的 类标记,返回T;
f)否则,按特征 A g A_g Ag的不同取值 a i a_i ai,依 A g = a i A_g=a_i Ag=ai将D分割为若干个非空子集 D i D_i Di,将 D i D_i Di中实例数最大的类作为标记,构建子节点,由节点和子节点构成树T,返回T。
g)对第 i i i个子节点,以 D i D_i Di为数据集,以 A − A g A-{A_g} A−Ag为特征集,递归的调用 a 步 − f 步 a步-f步 a步−f步,得到子树 T i T_i Ti,返回 T i T_i Ti。
3)ID3的局限性
ID3由 Ross Quinlan 在1986年提出,算法本身还存在很大的局限性:
- 采用信息增益做特征选择,会存在偏向于选择特征取值较多的特征;
- 无法处理处理连续变量;
- 无法对缺失值进行处理;
- 没有剪枝策略,容易过拟合;
为了克服上述不足,Ross Quinlan 对ID3算法进行了改进,这就是下面将要探讨的C4.5算法。
4)C4.5算法
C4.5重大的改进是,提出利用信息增益比(Information Gain Ratio)来做特征选择,解决ID3算法存在的特征偏向问题。
特征A对训练集D的信息增益比 g R ( D , A ) g_R(D,A) gR(D,A),为信息增益 g ( D , A ) g(D,A) g(D,A)与训练集D关于特征A的值的熵 H A ( D ) H_A(D) HA(D)之比,表达式为:
g R ( D , A ) = g ( D , A ) H A ( D ) g_R(D,A)=\frac{g(D,A)}{H_A(D)} gR(D,A)=HA(D)g(D,A)
其中 H A ( D ) = − ∑ i = 1 n D i D l o g 2 D i D H_A(D) = -\sum _{i=1}^n\frac{D_i}{D}log_2\frac{D_i}{D} HA(D)=−∑i=1nDDilog2DDi, n n n是特征A取值的个数。对于类别多的特征, H A ( D ) H_A(D) HA(D)的取值会偏大,用来平衡信息增益带来的偏倚。
C4.5对于连续性值的处理方式为我们熟知的特征离散化。假如n个样本的连续性特征A有m个取值。C4.5算法首先将m个取值从小到大排序为 a 1 , a 2 . . . a m a_1,a_2...a_m a1,a2...am,分别对相邻的两个样本取平均数,一共得到 m − 1 m-1 m−1个划分点,其中第 i i i个划分点为 a i + a i + 1 2 \frac{a_i+a_{i+1}}{2} 2ai+ai+1;然后对于m-1个划分点,分别计算以该划分点作为二元分类点时的信息增益,并选择信息增益最大的点作为该连续特征的二元离散分类点
对缺失值的处理,本质就是算法怎么填补缺失值,C4.5在缺失值处理也做了优化。样本中存在缺失值,会引起两个问题:第一,如何在特征值缺失的情况下进行特征选择,即存在缺失值特征的信息增益比该怎么计算?第二,特征选定之后,缺失样本该分到那个子节点中去?
对于第一个问题,C4.5的做法是,计算不含缺失值样本的特征A的信息增益比,乘上一个权重,权重为不含缺失样本占总样本的比例;对于第二个问题,C4.5的做法是,将缺失特征的样本同时划分入所有的子节点中,每个子节点所占的权重为每个该子节点样本占总样本的比例。
对于过拟合问题,C4.5采用后剪枝的方式来简化决策树。我们在CART树再一起讨论。
5)C4.5的局限性
虽然C4.5在ID3算法上进行了很大的改进,但是还是存在一些明显的局限性:
- 当特征的类别特别多时,生成决策树(多叉树)时,运行效率会变得非常低;
- 只能处理分类问题;
- 不管信息增益还是信息增益比,都拥有大量耗时的对数运算,甚至连续值还有排序运算,比较消耗算力;
下篇我们重点讨论CART算法如何优化C4.5所存在的这些局限性。
(欢迎大家在评论区探讨交流,也欢迎大家转载,转载请注明出处。)
上一篇:Scikit-learn 支持向量机库总结与简单实践
下一篇:决策树(Decision Tree)算法原理总结(二)