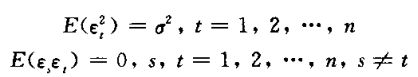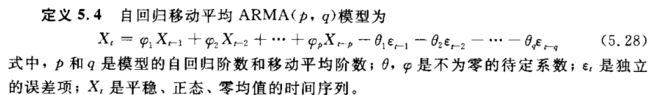读书笔记《MATLAB在时间序列分析中的应用》by 张善文
注:本篇博文是自己在阅读《MATLAB在时间序列分析中的应用》一书的记录,是非常棒的一本书,推荐研究时间序列的小伙伴学习!
前言
本书简明的介绍了时间序列及其相关领域的基本概念和基本理论,重在讲述有关基础理论和物理背景,避开了繁复的理论推导,结合MATLAB编程应用,介绍了MATLAB编程应用,介绍了MATLAB时间序列分析有关函数的功能和用法,并通过应用实例,阐述了如何利用这些函数解决工程应用中的问题。
第一章 时间序列及其分析概述
1.1.1 时间序列
时间序列取值一般有两种方式(1)X取观测时间点处的瞬时值
(2)X取相邻时间点期间的累积值
时间序列的广义定义为:有先后顺序的数据
时间序列的组成成分:长期趋势,季节变动,循环变动,不规则变动
1.1.3时间序列模型
1.确定型时间序列模型
实践表明,实际中的一个时间序列往往由加法,乘法,和混合三种模型变化形式的叠加或耦合而成的。
2.线性时间序列模型
AR,MA,ARMA,ARIMA
3.时间序列建模基本步骤
(1)用观测,调查,统计,抽样等方法取得被观测系统时间序列数据
(2)根据动态数据做相关图,进行相关分析,求自相关函数
(3)辨识合适的随机模型,进行曲线拟合,即使用通用随机模型拟合时间序列的观测数据
4.时间序列的参数估计基本步骤
(1)分析数据序列的变化特征
(2)选择模型形式和参数检验
(3)利用模型进行趋势预测
(4)评估预测结果并修正模型
1.3.4时间序列分析和数理统计学的区别
(1)数理统计学的样本值是对同一个随机变量进行n次独立重复试验的结果,或是n个相互独立,同分布的随机变量序列的一个实现.而时间序列则是某一随机过程的一次样本实现
(2)数理统计学中的回归模型描述的是因变量与其他自变量之间的统计静态依存关系;而时间序列分析中的自回归模型描述的是某一变量自身变化的统计规律性,是某一系统的现在行为与其历史行为之间的动态统计依存关系。
(3)在数理统计学中,进行统计推断的目的,主要是对一个随机变量的分布参数进行估计或假设检验;而在时间序列分析中,则是对某一时间序列建立统计模型。
第二章 时间序列的统计量
不同的统计量有不同的功能,例如:数据中心趋势度量的目的在于确定数据在数据分布线上分布的中心,即中心位置的度量。散布度量可以理解为序列中的数据偏离其数值中心的程度,也称作离差;极差为数据最大观测值与最小观测值之差,是对散布最简单的测量,但对野值十分敏感。中心矩是关于数学期望的矩,相关系数是两个随机变量间线性相依程度的度量。
2.1 MATLAB中常用的时间序列分析函数
C=max(X) %找出x序列的最大值
[C,I]=max(X) %找出X序列的最大值以C表示,该值在序列X中的位置以I显示
C=min(X)
[C,I]=min(X)
M=sum(X) %计算时间序列X的总和以M显示
M=sum(X,'double') %计算时间序列X的总和以M显示,M为double数据类型
M=sum(X,'native')
M=mean(X)
M=median(X)
M=geomean(X) %计算时间序列X的几何均值
M=harmmean(X) %计算时间序列X的调和均值
M=trimmean(X,percent) %对时间序列X进行排序后,去掉两端的部分极值,再对其计算算术平均值,参数
percent为去掉X中极值的比例
R=range(X) %计算时间序列的极差
L=length(X) %测量时间序列的长度,返回整数L
[C,L]=size(X) %要求时间序列为二维,测量时间序列的长度,输出参数C为维数,L为长度
N=norm(X) %计算时间序列的模
P=prod(X) %计算时间序列X的连乘值
C=cumsum(X) %计算时间序列X的累积总和值
C=cumprod(X) %计算时间序列X的累积连乘值
y=prctile(X,p) %计算X中大于p%的值,p的值介于0-1002.2 时间序列的重排序
M=sort(X,mode) %当参数mode='ascend'时,对时间序列x进行升序重排;当mode=‘descend’时,对时间序列x进行降序重排,当mode缺省时,默认进行升序重排
M=wrev(X) %得到x逆序排列的时间序列M
M=issorted(X) %若X为升序序列,则M=1,否则M=0
[b,m,n]=unique(x) %输出参数b为x的互异元素按升序重排,m为b中每一元素最后一次出现在x中的位置,n为x中各个元素在b中的位置
M=ismember(X1,X2) %输出参数M为与X1同维序列,对于i,若X1(i)属于X2,则M(i)=1;否则M(i)=0
B=sortrows(A) %对时间序列A按第一字符的字典顺序进行重排,的时间序列B
B=sortrows(A,column) %如果A中各个元素为字符串,则按每个字符串中第column个字符的字典顺序重排,得时间序列B
[B,C]=sortrows(A) %对时间序列A按第一字符的字典顺序进行重排,得时间序列B和B中各个元素在A中的位置序列C
y=linspace(a,b) %在实数a与b之间线性插入100个实数,得到一个长度为100的时间序列,包含a,b
y=linspace(a,b,n) %在实数a与b之间插入n个实数,得到一个长度(包括a,b)为n的序列
[xi,yi]=wcommon(x,y) %用来寻找两序列x与y中的公共元素,输出参数Xi与yi为由0和1组成的向量。
XLAG=lagmatrix(X,Lags) % 生成一个将X滞后Lags的与X同维的时间序列
y=wkeep(x,l,opt) %从时间序列x中提取长度为1的一个时间序列y。当输入参数opt='c'时,则从x的中间提取;当输入参数opt='l'时,则从x的左边提取;当输入参数opt='r'时,则从x的右边提取
y=wkeep(x,l) %默认时从中间提取2.3随机时间序列的生成
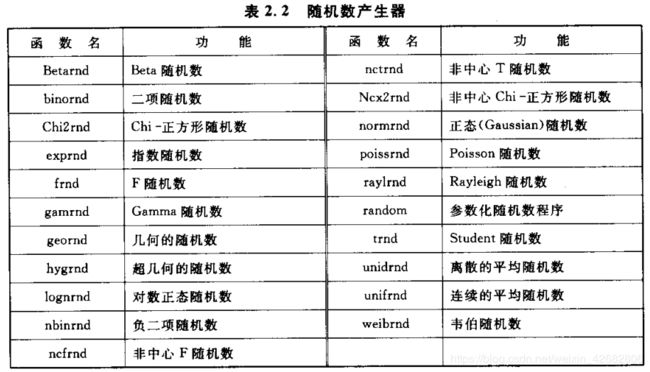
随机数生成器的基本方法:直接法,反转法,加绝对值法
y=rand %生成一个0-1之间的一个随机数
y=rand(1,m) %生成一个由m个0-1之间的实数组成的时间序列
y=rand(m) %生成一个0-1之间的m*m随机方阵
y=rand(m,n) %生成一个0-1之间的m*n随机矩阵
y=rand([m n]) %等价于上
y=rand(size(A)) %生成一个0-1之间与A同维的随机矩阵rand:生成均匀分布的随机时间序列
randn:生成正态分布的随机时间序列
说明:muw为R的均值;sigma为R的标准差;m,n两个正整数,分别表示生成随机时间序列R的行和列的大小;
v为多维时间序列的维数
R=normrnd(mu,sigma) %生成一个随机数,或生成均值为mu,标准差为sigma的多个随机数
R=normrnd(mu,sigma,1,n) %生成有n个数据,均值为mu,标准差为sigma的正态分布的时间序列
R=normrnd(mu,sigma,m,n) %生成一个均值为mu,标准差为sigma的正态分布的m*n随机矩阵
R=normrnd(mu,sigma,v) %生成一个均值为mu,标准差为sigma的正态分布的v维随机矩阵
R=normrnd(mu.sigma,m) %生成一个均值为mu,标准差为sigma的正态分布的m*m随机方阵
R=random('name',A1,A2,A3,m,n)
说明 A1,A2,A3 为分布参数矩阵,有时有些是不需要的
m,n:两个正整数,分别表示生成随机时间序列R的行和列的大小,当m=1时,即生成一个n个数组成的序列
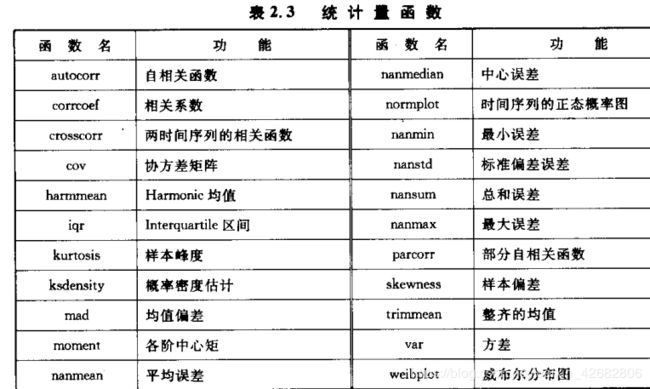
name:指定分布的名称2.4时间序列的统计量函数
y=mad(x) %计算时间序列x的平均绝对误差,即y=(abs(x-mean(x)))
y=mad(x,1) %等价于y=median(abs(x-median(x)))
k=kurtosis(x) %计算时间序列x的峰度
k=kurtosis(x,flag) %指定是否校正系统偏差,flag=0时进行校正,flag=1时不校正,缺省为不校正y=skewness(x) %计算时间序列的偏度,用于衡量x的对称性,对于正态分布的偏度为0
y=skewness(x,flag) %指定是否校正系统偏差,flag=0时进行校正,flag=1时不校正
M=var(X) %除以(n-1),无偏方差
M=var(X,0) %同上
M=var(X,1) %除以n,有偏方差
M=std(x) %无偏标准差
M=std(x,0)
M=std(x,1) %有偏标准差
M=moment(x,order) %计算时间序列x的order阶中心矩,参数order为中心矩的阶次
M=cov(x) %计算时间序列x的自协方差
M=cov(X1,X2) %计算两时间序列x1和x2的协方差,得2*2协方差矩阵M。其中矩阵M的主对角线的值分别为X1和X2的自协方差M=corrcoef(X) %计算时间序列x的自相关系数,结果为1
M=corrcoef(X1,X2) %计算两时间序列X1和X2的相关系数M。其中M在0-1
说明:Series为时间序列
nLags为延迟,当nLags为缺省时,计算ACF时在延迟点0,1,2,3......T,而T=min(20,length(Series)-1)
nSTDs 表示计算出的相关系数ACF估计误差的标准差
M:表示Lags的非负整数,当M缺省时,autocorr假设为高斯白噪声
ACF为相关系数
Lags 为对应于ACF的延迟
Bounds:置信区间的近似上下限,假设序列是MA(M)过程
autocorr(Series,nLags,M,nSTDs)
[ACF,Lags,Bounds]=autocorr(Series,nLags,M,nSTDs)
自相关函数是时间序列的当前值与过去值之间的相关函数,通过估计自相关函数,可以了解时间序列的两个特征:时间趋势和平稳性。
crosscorr(Series1,Series2,nLags,nSTDs) %计算并描绘两时间序列的相关函数,画图时无置信区间边界,而nSTDs=0
[XCF,Lags,Bounds]=crosscorr(Series1,Series2,nLags,nSTDs) %计算并描绘两时间序列在延迟为nLags,估计误差的标准差为nSTDs时的相关函数
说明: Series1,Series2 为时间序列
nLags为延迟
XCF:相关系数
Lags:对应于XCF的延迟
Bounds:置信区间的近似上下限,假设两序列完全不相关
parcorr(Series,nLags,R,nSTDs)
[PartialACF,Lags,Bounds]=parcorr(Series,nLags,R,nSTDs)
说明: Series为时间序列
nLags为延迟, nSTDs表示计算出的相关函数ACF估计误差的标准差
R 表示Lags的非负整数,当R=[]或缺省时,表示autocorr假设为AR(R)过程
PartialACF:相关系数
Lags:对应于ACF的延迟
Bounds:置信区间的近似上下限,假设序列是AR(R)过程[f,xi]=ksdensity(x) %计算时间序列x中样本数据的概率密度,f为样本点xi处的概率密度
f=ksdensity(x,xi) %f为样本点xi处的概率密度
normplot(x) %描绘时间序列的正态概率图
h=normplot(x) %返回一个图中直线句柄h
weibplot(x) %生成威布尔概率分布图,要求x的值大于0
r=weibplot(x) %返回一个图中直线句柄r2.5 时间序列的分布函数
P=cdf('name',x,A1.A2,A3) %计算时间序列累积分布函数
说明: name为分布函数名称,x为时间序列
A1,A2,A3为分布函数参数
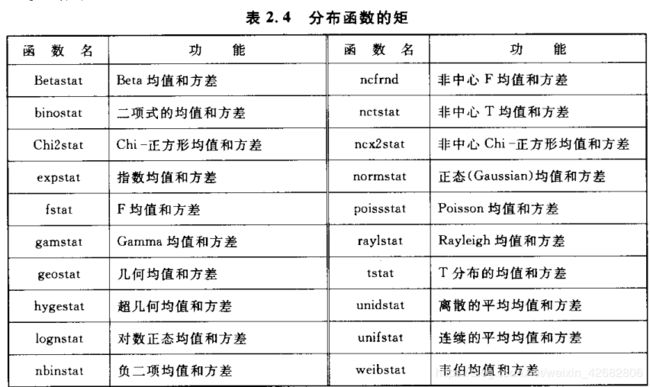
p=pdf('name',x,A1,A2,A3) %计算时间序列指定分布的概率密度函数在统计工具箱中,用‘stat’结尾的函数可以计算给定参数的某种分布的均值和方差
2.6时间序列趋势项提取
y=detrend(X) %消除时间序列中的线性趋势项
y=detrend(X,'constant') %消除时间序列中的均值
y=detrend(X,'linear',bp) %分段消除时间序列中的线性趋势项,bp为分段点向量第三章 时间序列插值与差分
3.4MATLAB 中插值函数及其应用
3.4.1一维内插函数
dyaddown:对时间序列进行二元采样,每隔一个元素提取一个元素,得到一个降采样时间序列
dyadup :对时间序列进行二元插值,每隔一个元素插入一个0元素,得到一个时间序列
interp :对时间序列进行整数倍插值,使得时间序列曲线更光滑
y=dyaddown(x,EVENODD) %当EVENODD=0时,从x中第二个元素开始偶采样。当EVENODD=1时,从x中第一个元素
开始奇采样
y=dyaddown(x) %EVENODD缺省,按从x中第二个元素开始采样
y=dyadup(x,EVENODD) %当EVENODD=0时,从x中第一个元素后开始偶插入0。当EVENODD=1时,从x中第一个元
素前开始奇插入
y=dyadup(x) %EVENODD缺省,按从x中第一个元素后开始插入
说明:x为时间序列;r为插入点的倍数; l为插值滤波器长度;alpha为滤波器的截止频率
y为插值后得到的时间序列 ; b为低通插值滤波器的系数
y=interp(x,r) %在x中插入一些数据,使得插值后的序列y的长度为x的r倍
y=interp(x,r,l,alpha) %插值后得到的序列y的长度为x的r倍
[y,b]=interp(x,r,l,alpha) %插值后同时得到一个低通插值滤波器的系数,长度为2rl+1
downsample:对时间序列重采样,在原时间序列中等间隔地取出一些项,得到新序列
decimate :对时间序列进行整数倍降采样处理,使得时间序列的长度降低
y=downsample(x,n) %从第一项开始,等间隔n对x采样,得到的序列为y
y=downsample(x,n,phase) %从第phase+1项开始,等间隔n对x采样,得到的序列为y
y=decimate(x,r) %将时间序列x的采样频率降低为原来的1/r
y=decimate(x,r,n) %采用n阶chebyshevI型低通滤波器
y=decimate(x,r,'fir') %采用30阶的FIR型低通滤波器来压缩频带,对时间序列进行整数倍抽取
y=decimate(x,r,n,'fir') %指定当对时间序列进行整数倍抽取时,采用n点FIR型低通滤波器来压缩频带
说明: x为时间序列,r为采样要降低的倍数
n为指定所采用的chebyshevI型低通滤波器的阶数
‘fir’: FIR滤波器resample:对时间序列进行重采样
interpl :一维时间序列分段线性内插
y=resample(x,p,q)
y=resample(x,p,q,n)
y=resample(x,p,q,,n,beta)
y=resample(x,p,q,b)
[y,b]=resample(x,p,q)
说明: x为时间序列 ,p,q为正整数,指定重采样的长度的倍数
n为指定所采用的chebyshevIIR型低通滤波器的阶数,滤波器的长度与n成比例
beta:设计低通滤波器时使用Kaiser窗的参数,缺省值为5
y:重采样得到的序列,y的长度为原来的序列x的长度的p/q倍
b:输出参数b为所使用的滤波器的系数向量3.4.2样条插值
3.4.3微分和差分
diff: 计算时间序列的微分
polyde: 计算多项式的微分
y=diff(x) %计算时间序列x的一阶差分值
y=diff(x,n) %计算时间序列x的n阶差分值
y=polyder(l) %返回以向量L所表示的多项式的微分
y=polyval(l,xn) %向量L所表示的多项式L(x)在xn点处的值3.5插值差分的应用
(1)重构连续函数
(2)利用微分求函数的极值点
(3)曲线插值
第四章 时间序列拟合
拟合分析是研究变量之间相关关系的一种数学方法,使用这种方法可以由一个随机变量取得的值来估计另一个变量所取的值。
4.1 拟合问题的提法
一般将函数拟合也称为曲线拟合,曲线拟合也称为曲线回归。实际中经常用到的三种拟合是曲线拟合,线性/非线性回归分析和自回归移动平均(ARMA)模型。
曲线拟合与前述的曲线插值有许多相似之处,但是这两者最大的区别在于曲线拟合要找出一个曲线方程式,而曲线插值仅是要求出内插点函数值即可。
在进行函数拟合时,要回答以下几个问题
(1)采用什么函数模型
(2)模型的结构参数是什么
(3)参数的估计值如何计算
(4)估计参数的离差
4.2最小平方拟合
4.2.1一元线性拟合
一元线性拟合研究的是寻找一个因变量与一个自变量之间的线性关系
4.2.2最小二乘多项式拟合
4.3函数的最优平方拟合
4.4MATLAB下时间序列拟合函数
lsline :在当前图中添加最小二乘拟合曲线
lpc:线性预测
regress:多重线性拟合
robustfit: 稳健线性拟合
lsline %在当前图中添加最小二乘拟合曲线
h=lsline %在当前图中添加最小二乘拟合曲线,并返回直线对象句柄
[a,g]=lpc(x,p) %估计线性预测
说明:x为时间序列 ,p为线性预测器的阶数
a为预测系数, g为预测误差
b=regress(y,x) %返回x处y的最小二乘拟合值,得到线性函数中的待定系数
[b,bint]=regress(y,x) %返回拟合系数的95%置信区间bint
[b,bint,r]=regress(y,x) %返回残差r
[b,bint,r,rint]=regress(y,x) %返回残差r的置信区间
[...]=regress(y,x,alpha) %返回参数alpha表示置信区间为(1-alpha)
说明:拟合的线性函数的一般表达式为:y=Xb+r
y:n*1观察值
x:n*p拟合矩阵
alpha:置信度参数
b:线性函数的一次项系数p*1矩阵
bint:置信区间
r:残差,n*1矩阵
rint:残差的范围
b=robust(x,y) %将y表示为x的列数据的函数,返回系数估计矢量b
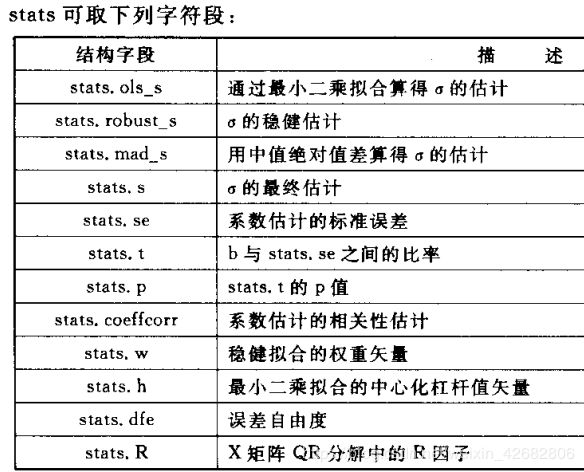
[b,stats]=robustfit(x,y) %得到系数估计矢量b和一个stats结构
[b,stats]=robustfit(x,y,'wfun','tune','const')%指定一个加权系数,一个调协常数和是否显示常数项
说明: y为n*1观察值,x为n*p拟合矩阵 ‘wfun’为加权函数 ‘tune’为调协常数
‘const’为是否显示常数项 b为线性函数的一次项系数p*1矩阵
stats:字符段的结构 bint:置信区间
r:残差,n*1矩阵 rint:残差的范围
polyfit:多项式曲线拟合
polyval:由多项式系数矢量估计自变量的函数值
注:polyval是与polyfit有关的函数,是用来做多项式函数计算,由polyfit算出多项式的各个系数后,可以用polyval计算多项式的函数值
p=polyfit(x,y,n) %在最小二乘意义下,由x和y拟合一个n次多项式,返回多项式高次到低次排列的系数行向量
p,p的长度为n+1
[p,S]=polyfit(x,y,n) %同上
[p,S,mu]=polyfit(x,y,n) %
说明:x为自变量矢量 y为自变量矢量x对应的观察值
n为拟合多项式的次数 p为拟合多项式系数矢量
S为误差参数结构 mu为x的均值和标准差
y=polyval(p,x) %p为n阶多项式的系数,n为p的长度,计算多项式在x点的值以y表示
y=polyval(p,x,[],mu) %x的均值和标准差为mu时估计多项式在x点的值
[y,delta]=polyval(p,x,S)
[y,delta]=polyval(p,x,S,mu)
说明: p为多项式系数矢量 x为自变量矢量 mu为x的均值和标准差
S为polyfit函数中得到误差参数 y为自变量矢量x对应的函数值
delta为估计误差polytool:多项式拟合及预测交互式绘图
nlinfit: 非线性最小二乘数据拟合
polytool(x,y) %将列矢量x和y拟合为曲线,并显示其交互式图形
polytool(x,y,n) %拟合初始阶次为n的多项式
polytool(x,y,n,alpha) %同时绘出预测值的100(1-alpha)%置信区间
beta=nlinfit(x,y,fun,beta0) %用最小二乘法估计非线性函数fun的待定系数,返回beta为拟合得到的系数
向量
[beta,r,J]=nlinfit(x,y,fun,beta0) % 返回r,J,r和J用于nintool函数的预测值估计
[...]=nlinfit(x,y,fun,beta0,options) %利用参数结构options拟合
说明:
x为自变量矢量 y为自变量矢量x对应的函数值
fun:用户给定的函数结构,函数系数待定 beta0:函数系数的初始值
options:用于控制nlinfit函数所使用算法的参数结构
beta:拟合得到的系数向量 r,J:r为残差,J为一个雅可比矩阵lsqcurvefit:最小二乘意义上的非线性曲线拟合
polyconf:多项式评估和置信区间估计
ridge:脊回归参数估计
4.5 时间序列拟合的应用
第五章 ARMA时间序列
5.1 白噪声时间序列
5,2自回归模型
5.2.1自回归模型概述
定义:
5.2.2 AR(p)的自相关函数
(1)自协方差函数
(2)自相关函数
5.2.3序列的自相关系数的作用
对现有的时间序列数据无需任何了解,就能得到其自相关系数,这些系数可以用来揭示所研究的时间序列的特性,并能帮助选定一个合适的模型。
5.2.4 AR(p)模型的平稳解
5.3移动平均模型
定义:
模型含义:MA(q)模型用过去各个时期的随机干扰或预测误差的线性组合来表达当前预测值。
5.4自回归移动平均模型
5.4.1 ARMA(p,q)序列
定义:
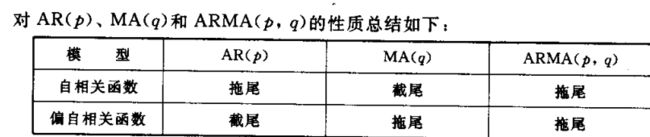
三种模型的性质小结
5.5整合自回归移动平均模型(ARIMA)
一般人们所关注的有趋势和季节,循环成分的时间序列都是非平稳的,这时候就需要对时间序列进行差分来消除这些使序列不平稳的成分,而使其变成平稳的时间序列,并估计ARMA模型,估计之后再转变该模型,使之适应于差分之前的序列模型,这个过程与差分过程相反,所以称为整合的ARMA模型。即ARIMA模型。
5.6时间序列模型预测
5.7模型参数最小二乘估计
5.8MATLAB下ARMA序列分析函数
ar :估计AR时间序列模型参数
m=ar(y,n) %估计AR时间序列模型参数
[m,refl]=ar(y,n.approach,window) %选择估计方法和设置窗,估计模型参数
[m,refl]=ar(y,n,approach,window,Prop1,Value1,Prop2,Value2,...) %根据property及其值估计AR模型
参数
说明: AR时间序列模型为A(q)y(t)=e(t)
y为时间序列结构,由iddata函数得到
n为AR模型阶数 approach为估计时采用的方法
window:包含AR模型信息m=armax(data,orders)
m=armax(data,'na',na,'nb',nb,'nc',nc,'nk',nk)
m=armax(data,orders,'Property1',Value1,...,'PropertyN','ValueN')garchar: 将有限阶的ARMA模型转换为无限阶的自回归AR模型
garchma:将有限阶的ARMA模型转换为无限阶的自回归MA模型
InfiniteAR=garchar(AR,MA,NumLags)
InfiniteMA=garchma(AR,MA,NumLags)garchfit:一元ARMA模型参数估计
garchcount: 计算ARMA模型的估计参数
lpc:计算AR模型的系数
prony:计算ARMA模型的系数
5.9ARMA序列分析的应用
第六章 时间序列的时频特性分析
第七章 时间序列的统计分析
第八章 时间序列的小波变换
注:后三章知识暂时用不到,战略性放弃!